Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T05:39:50.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Liquid velocity fluctuations and energy spectra in three-dimensional buoyancy-driven bubbly flows

Published online by Cambridge University Press:  17 December 2019

Vikash Pandey ,
Rashmi Ramadugu  and
Prasad Perlekar Open the ORCID record for Prasad Perlekar [Opens in a new window]
Vikash Pandey
Affiliation:
TIFR Centre for Interdisciplinary Sciences, Tata Institute of Fundamental Research, Hyderabad, 500107, India
Rashmi Ramadugu
Affiliation:
TIFR Centre for Interdisciplinary Sciences, Tata Institute of Fundamental Research, Hyderabad, 500107, India
Prasad Perlekar*
Affiliation:
TIFR Centre for Interdisciplinary Sciences, Tata Institute of Fundamental Research, Hyderabad, 500107, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

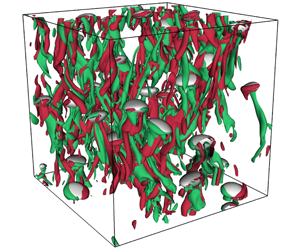
We present a direct numerical simulation (DNS) study of pseudo-turbulence in buoyancy-driven bubbly flows for a range of Reynolds ($150\leqslant Re\leqslant 546$) and Atwood ($0.04\leqslant At\leqslant 0.9$) numbers. We study the probability distribution function of the horizontal and vertical liquid velocity fluctuations and find them to be in quantitative agreement with the experiments. The energy spectrum shows a $k^{-3}$ scaling at high $Re$ and becomes steeper on reducing $Re$. To investigate spectral transfers in the flow, we derive the scale-by-scale energy budget equation. Our analysis shows that, for scales smaller than the bubble diameter, the net transfer because of the surface tension and the kinetic energy flux balances viscous dissipation to give $k^{-3}$ scaling of the energy spectrum for both low and high $At$.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Turbulent Flows: Turbulence simulation
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , R6
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alméras, E., Mathai, V., Sun, C. & Lohse, D. 2019 Mixing induced by a bubble swarm rising through incident turbulence. Intl J. Multiphase Flow 114, 316–322.CrossRefGoogle Scholar
Alméras, E., Mathai, V., Lohse, D. & Sun, C. 2017 Experimental investigation of the turbulence induced by a bubble swarm rising within incident turbulence. J. Fluid Mech. 825, 1091–1112.CrossRefGoogle Scholar
Aniszewski, W. et al. 2019 PArallel, Robust, Interface Simulator (PARIS), hal-02112617. Available at: https://hal.sorbonne-universite.fr/hal-02112617.Google Scholar
Bhaga, D. & Weber, M. E. 1981 Bubbles in viscous liquids: shapes, wakes and velocities. J. Fluid Mech. 105, 61–85.CrossRefGoogle Scholar
Biferale, L., Perlekar, P., Sbragaglia, M. & Toschi, F. 2012 Convection in multiphase fluid flows using lattice Boltzmann methods. Phys. Rev. Lett. 108, 104502.CrossRefGoogle ScholarPubMed
Bunner, B. & Tryggvason, G. 2002a Dynamics of homogeneous bubbly flows. Part 1. Rise velocity and microstructure of the bubbles. J. Fluid Mech. 466, 17–52.CrossRefGoogle Scholar
Bunner, B. & Tryggvason, G. 2002b Dynamics of homogeneous bubbly flows. Part 2. Velocity fluctuations. J. Fluid Mech. 466, 53–84.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. M. & Zang, T. A. 2012 Spectral Methods in Fluid Dynamics. Springer-Verlag.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–202.CrossRefGoogle Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops and Particles. Academic Press.Google Scholar
Deckwer, W.-D. 1992 Bubbles Column Reactors. Wiley.Google Scholar
Elghobashi, S. 2019 Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 51, 217–244.CrossRefGoogle Scholar
Frisch, U. 1997 Turbulence, A Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Gonnermann, H. M. & Manga, M. 2007 The fluid mechanics inside a volcano. Annu. Rev. Fluid Mech. 39, 321–356.CrossRefGoogle Scholar
Joseph, D. D. 1976 Stability of Fluid Motions II. Springer.CrossRefGoogle Scholar
Lance, M. & Bataille, J. 1991 Turbulence in the liquid phase of a uniform bubbly airwater flow. J. Fluid Mech. 222, 95–118.CrossRefGoogle Scholar
Larue De Tournemine, A.2001 Etude expérimentale de l’effet du taux de vide en écoulement diphasique á bulles. PhD thesis, Institut National Polytechnique de Toulouse.Google Scholar
Mathai, V., Huisman, S. G., Sun, C., Lohse, D. & Bourgoin, M. 2018 Dispersion of air bubbles in isotropic turbulence. Phys. Rev. Lett. 121 (5), 054501.CrossRefGoogle ScholarPubMed
Mathai, V., Lohse, D. & Sun, C. 2020 Bubble and buoyant particle laden turbulent flows. Annu. Rev. Condens. Matter Phys. 11, (in press).Google Scholar
Mendez-Diaz, S., Serrano-Garcia, J. C., Zenit, R. & Hernández-Cordero, J. A. 2013 Power spectral distributions of pseudo-turbulent bubbly flows. Phys. Fluids 25 (4), 043303.CrossRefGoogle Scholar
Mercado, J. M., Gómez, D. G., Gils, D. V., Sun, C. & Lohse, D. 2010 On bubble clustering and energy spectra in pseudo-turbulence. J. Fluid Mech. 650, 287–306.CrossRefGoogle Scholar
Mudde, R. F. 2005 Gravity-driven bubbly flows. Annu. Rev. Fluid Mech. 37, 393–423.CrossRefGoogle Scholar
Pandit, R. et al. 2017 An overview of the statistical properties of two-dimensional turbulence in fluids with particles, conducting fluids, fluids with polymer additives, binary-fluid mixtures, and superfluids. Phys. Fluids 29, 111112.CrossRefGoogle Scholar
Pandit, R., Perlekar, P. & Ray, S. S. 2009 Statistical properties of turbulence: an overview. Pramana 73 (1), 157–191.CrossRefGoogle Scholar
Perlekar, P. 2019 Kinetic energy spectra and flux in turbulent phase-separating symmetric binary-fluid mixtures. J. Fluid Mech. 873, 459–474.CrossRefGoogle Scholar
Perlekar, P., Mitra, D. & Pandit, R. 2006 Manifestations of drag reduction by polymer additives in decaying, homogeneous, isotropic turbulence. Phys. Rev. Lett. 97, 264501.CrossRefGoogle ScholarPubMed
Perlekar, P., Mitra, D. & Pandit, R. 2010 Direct numerical simulations of statistically steady, homogeneous, isotropic fluid turbulence with polymer additives. Phys. Rev. E 82, 066313.Google ScholarPubMed
Pivello, M. R., Villar, M. M., Serfaty, R., Roma, A. M. & Silveira-Neto, A. 2014 A fully adaptive front tracking method for the simulation of two phase flows. Intl J. Multiphase Flow 58, 72–82.CrossRefGoogle Scholar
Pope, S. 2012 Turbulent Flows. Cambridge University Press.Google Scholar
Prakash, V.N., Mercado, J.M., van Wijngaarden, L., Mancilla, E., Tagawa, Y., Lohse, D. & Sun, C. 2016 Energy spectra in turbulent bubbly flows. J. Fluid Mech. 791, 174–190.CrossRefGoogle Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.CrossRefGoogle Scholar
Risso, F. 2011 Theoretical model for k -3 spectra in dispersed multiphase flows. Phys. Fluids 23 (1), 011701.CrossRefGoogle Scholar
Risso, F. 2016 Physical interpretation of probability density functions of bubble-induced agitation. J. Fluid Mech. 809, 240–263.CrossRefGoogle Scholar
Risso, F. 2018 Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50, 25–48.CrossRefGoogle Scholar
Roghair, I., Mercado, J. M., Annaland, M. V. S., Kuipers, H., Sun, C. & Lohse, D. 2011 Energy spectra and bubble velocity distributions in pseudo-turbulence: numerical simulations versus experiments. Intl J. Multiphase Flow 37 (9), 1093–1098.CrossRefGoogle Scholar
Rycroft, C. H. 2009 Voro++: a three-dimensional Voronoi cell library in C++. Chaos: An Interdisciplinary Journal of Nonlinear Science 19 (4), 041111.CrossRefGoogle ScholarPubMed
Shukla, I., Kofman, N., Balestra, G., Zhu, L. & Gallaire, F. 2019 Film thickness distribution in gravity-driven pancake-shaped droplets rising in a Hele-Shaw cell. J. Fluid Mech. 874, 1021–1040.CrossRefGoogle Scholar
Tagawa, Y., Roghair, I., Prakash, V. N., van Sint Annaland, M., Kuipers, H., Sun, C. & Lohse, D. 2013 The clustering morphology of freely rising deformable bubbles. J. Fluid Mech. 721, R2.CrossRefGoogle Scholar
Tchoufag, J., Magnaudet, J. & Fabre, D. 2014 Linear instability of the path of a freely rising spheroidal bubble. J. Fluid Mech. 751, R4.CrossRefGoogle Scholar
Tripathi, M. K., Sahu, K. C. & Govindarajan, R. 2015 Dynamics of an initially spherical bubble rising in quiescent liquid. Nat. Commun. 6, 6268.CrossRefGoogle ScholarPubMed
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y.-J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169 (2), 708–759.CrossRefGoogle Scholar
Valente, P. C., da Silva, C. B. & Pinho, F. T. 2014 The effect of viscoelasticity on the turbulent kinetic energy cascade. J. Fluid Mech. 760, 39–62.CrossRefGoogle Scholar
Welch, P. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15 (2), 70–73.CrossRefGoogle Scholar
Wu, M. & Gharib, M. 2002 Experimental studies on the shape and path of small air bubbles rising in clean water. Phys. Fluids 14 (7), L49–L52.CrossRefGoogle Scholar

Pandey et al. supplementary movie 1

Time evolution of bubbles for our simulations R1 (Movie1.m4v). The bubbles are initially spherical in shape and their center-of-mass are distributed randomly over the entire simulation domain. The time evolution is shown from $t=0$ to $t=54 \tau_\lambda$.

Download Pandey et al. supplementary movie 1(Video)
Video 6.3 MB

Pandey et al. supplementary movie 2

Time evolution of bubbles for our simulations R4 (Movie2.m4v). The bubbles are initially spherical in shape and their center-of-mass are distributed randomly over the entire simulation domain. The time evolution is shown from $t=0$ to $t=27 \tau_\lambda$ .

Download Pandey et al. supplementary movie 2(Video)
Video 5.4 MB

Pandey et al. supplementary movie 3

Time evolution of bubbles for our simulations R6 (Movie3.m4v). The bubbles are initially spherical in shape and their center-of-mass are distributed randomly over the entire simulation domain. The time evolution is shown from $t=0$ to $t=20 \tau_\lambda$.

Download Pandey et al. supplementary movie 3(Video)
Video 6.3 MB