Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T22:53:57.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Liquid toroidal drop in compressional Stokes flow

Published online by Cambridge University Press:  23 November 2015

Michael Zabarankin ,
Olga M. Lavrenteva  and
Avinoam Nir
Michael Zabarankin*
Affiliation:
Department of Mathematical Sciences, Stevens Institute of Technology, Castle Point on Hudson, Hoboken, NJ 07030, USA
Olga M. Lavrenteva
Affiliation:
The Wolfson Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
Avinoam Nir
Affiliation:
The Wolfson Department of Chemical Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The deformation of an immiscible toroidal drop embedded in axisymmetric compressional Stokes flow is analysed via the boundary integral formulation in the case of equal viscosity. Numerical simulations are performed for the drop having initially the shape of a torus with circular cross-section. 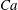The quasi-stationary dynamic simulations reveal that, when the viscous forces, proportional to the intensity of the flow, are relatively weak compared with the surface tension (the ratio of these forces is characterized by the capillary number, $Ca$), three different scenarios of drop evolution are possible: indefinite expansion of the liquid torus, contraction to the centre and a stationary toroidal shape. When the intensity of the flow is low, the stationary shapes are shown to be close to circular tori. Once the outer flow strengthens, the cross-section of the stationary torus assumes first an elliptic and then an egg-like shape. For the capillary number greater than a critical value, 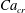$Ca_{cr}$, toroidal stationary shapes were not found. Remarkably, 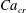$Ca_{cr}$ is close to the critical capillary number found previously for a simply connected drop flattened in compressional flow. Thus, a new example of non-uniqueness of stationary drop shape in viscous flow is obtained. Approximate stationary solutions in the form of tori with circular and elliptic cross-sections are obtained by minimizing the normal velocity over the drop interface. They are shown to be in good agreement with the stationary shapes from quasi-dynamic simulations for the corresponding intervals of the capillary number.

JFM classification

Mathematical Foundations: Computational methods Drops and Bubbles: Drops Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 372 - 400
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aris, R. 1962 Vectors, Tensors and Basic Equations of Fluid Mechanics. Prentice-Hall.Google Scholar
Baumann, N., Joseph, D. D., Mohr, P. & Renardy, Y. 1992 Vortex rings of one fluid in another in free fall. Phys. Fluids A 4 (3), 567–580.Google Scholar
Bosse, T., Kleiser, L., Härtel, C. & Meiburg, E. 2005 Numerical simulation of finite Reynolds number suspension drops settling under gravity. Phys. Fluids 17 (3), 037101.Google Scholar
Champion, J. A., Katare, Y. K. & Mitragotri, S. 2007 Particle shape: a new design parameter for micro- and nanoscale drug delivery carriers. J. Control. Release 121 (1–2), 3–9.CrossRefGoogle ScholarPubMed
Dendukuri, D., Tsoi, K., Hatton, T. A. & Doyl, P. S. 2005 Controlled synthesis of nonspherical microparticles using microfluidics. Langmuir 21, 2113–2116.Google Scholar
Deshmukh, S. D. & Thaokar, R. M. 2013 Deformation and breakup of a leaky dielectric drop in a quadrupole electric field. J. Fluid Mech. 731, 713–733.Google Scholar
Fontelos, M. A., Garcia-Garrido, V. J. & Kindelian, U. 2011 Evolution and breakup of viscous rotating drops. SIAM J. Appl. Math. 71, 1941–1964.Google Scholar
Ghazian, O., Adamiak, K. & Castle, G. S. P. 2013 Numerical simulation of electrically deformed droplets less conductive than ambient fluid. Colloid. Surf. A 423, 27–34.Google Scholar
Gulliver, R. 1984 Tori of prescribed mean curvature and the rotating drop. In Variational Methods for Equilibrium Problems of Fluids (Trento, 1983), Astérisque 118, pp. 167–179. Soc. math. de France, Paris.Google Scholar
Heine, C.-J. 2006 Computations of form and stability of rotating drops with finite elements. IMA J. Numer. Anal. 26, 723–751.Google Scholar
Hynd, R. & MacCuan, J. 2006 On toroidal rotating drops. Pacific J. Math. 224 (3), 279–289.Google Scholar
Khuri, S. A. & Wazwaz, A. M. 1997 On the solution of a partial differential equation arising in Stokes flow. Appl. Maths Comput. 85 (2–3), 139–147.Google Scholar
Kojima, M., Hinch, E. J. & Acrivos, A. 1984 The formation and expansion of a toroidal drop moving in a viscous fluid. Phys. Fluids 27 (1), 19–32.Google Scholar
Machu, G., Meile, W., Nitsche, L. & Schaflinger, U. 2001a The motion of a swarm of particles traveling through a quiescent, viscous fluid. Z. Angew. Math. Mech. 81 (S3), 547–548.Google Scholar
Machu, G., Meile, W., Nitsche, L. C. & Schaflinger, U. 2001b Coalescence, torus formation and breakup of sedimenting drops: experiments and computer simulations. J. Fluid Mech. 447, 299–336.Google Scholar
Mehrabian, H. & Feng, J. J. 2013 Capillary breakup of a liquid torus. J. Fluid Mech. 717, 281–292.Google Scholar
Nurse, A. K., Coriell, S. R. & McFadden, G. B. 2015 On the stability of rotating drops. J. Res. Natl Inst. Stand. Technol. 120, 74–101.Google Scholar
Pairam, E. & Fernández-Nieves, A. 2009 Generation and stability of toroidal droplets in a viscous liquid. Phys. Rev. Lett. 102, 234501.Google Scholar
Pairam, E., Vallamkond, J., Koning, V., Benjamin, C., van Zuiden, B. C., Ellis, P. W., Bates, M. A., Vitelli, V. & Fernández-Nieves, A. 2013 Stable nematic droplets with handles. Proc. Natl Acad. Sci. USA 110 (23), 9295–9300.CrossRefGoogle ScholarPubMed
Pell, W. H. & Payne, L. E. 1960 a On Stokes flow about a torus. Mathematika 7, 78–92.Google Scholar
Plateau, J. 1857 I. Experimental and theoretical researches on the figures of equilibrium of a liquid mass withdrawn from the action of gravity. Third series. Phil. Mag. 4 14 (90), 1–22.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. p. 272. Cambridge University Press.Google Scholar
Rallison, J. M. & Acrivos, A. 1978 A numerical study of the deformation and burst of a viscous drop in an extensional flow. J. Fluid Mech. 89, 191–200.Google Scholar
Renardy, Y., Popinet, S., Duchemin, L., Renardy, M., Zaleski, S., Josserand, C., Drumright-Clarke, M. A., Richard, D., Clanet, C. & Quéré, D. 2003 Pyramidal and toroidal water drops after impact on a solid surface. J. Fluid Mech. 484, 69–83.Google Scholar
Ruszczyński, A. 2011 Nonlinear Optimization. Princeton University Press.Google Scholar
Senyuk, B., Liu, Q., He, S., Kamien, R. D., Kusner, R. B., Lubensky, T. C., Ivan, I. & Smalyukh, I. I. 2013 Topological colloids. Nature 493, 200–205.Google Scholar
Shum, H. C., Abate, A. R., Lee, D., Studart, A. R., Wang, B., Chen, Ch.-H., Thiele, J., Shah, R. K., Krummel, A. & Weitz, D. A. 2010 Droplet microfluidics for fabrication of non-spherical particles. Macromol. Rapid Commun. 31, 108–118.Google Scholar
Slobozhanin, L. A. 1968 Hydrostatics in weak force fields. On annular figures of equilibrium of a rotating liquid and on their stability. Fluid Dyn. 3, 41–45.Google Scholar
Sostarecz, M. C. & Belmonte, A. 2003 Motion and shape of a viscoelastic drop falling through a viscous fluid. J. Fluid Mech. 497, 235–252.Google Scholar
Stone, H. A. & Leal, L. G. 1989 A note concerning drop deformation and breakup in biaxial extensional flows at low Reynolds numbers. J. Colloid Interface Sci. 133, 340–347.Google Scholar
Texier, D. B., Piroird, K., Quéré, D. & Clanet, C. 2013 Inertial collapse of liquid rings. J. Fluid Mech. 717, R3 (10 pages).CrossRefGoogle Scholar
Velev, O. D., Lenhoff, A. M. & Kaler, E. W. 2000 A class of microstructured particles through colloidal crystallization. Science 287 (5461), 2240–2243.Google Scholar
Wang, B., Shum, H. C. & Weitz, D. A. 2009 Fabrication of monodisperse toroidal particles by polymer solidification in microfluidics. ChemPhysChem 10, 641–645.Google Scholar
Yao, Zh. & Bowick, M. J. 2011 The shrinking instability of toroidal liquid droplets in the Stokes flow regime. Eur. Phys. J. E 34, 32.Google Scholar
Zabarankin, M. 2008 The framework of $k$ -harmonically analytic functions for three-dimensional Stokes flow problems. Part I. SIAM J. Appl. Maths 69 (3), 845–880.Google Scholar
Zabarankin, M. 2012 Cauchy integral formula for generalized analytic functions in hydrodynamics. Proc. R. Soc. Lond. A 468 (2148), 3745–3764.Google Scholar
Zabarankin, M. 2013 A liquid spheroidal drop in a viscous incompressible fluid under a steady electric field. SIAM J. Appl. Maths 73 (2), 677–699.Google Scholar
Zabarankin, M. & Krokhmal, P. 2007 Generalized analytic functions in 3D Stokes flows. Q. J. Mech. Appl. Maths 60 (2), 99–123.Google Scholar
Zabarankin, M. & Nir, A. 2011 Generalized analytic functions in an extensional Stokes flow with a deformable drop. SIAM J. Appl. Maths 71 (4), 925–951.Google Scholar
Zabarankin, M., Smagin, I., Lavrenteva, O. M. & Nir, A. 2013 Viscous drop in compressional Stokes flow. J. Fluid Mech. 720, 169–191.Google Scholar
Zhao, S. & Tao, J. 2013 Instability of a rotating liquid ring. Phys. Rev. E 88, 033016.Google Scholar