Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T15:41:02.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of confined flow around a 180-degree sharp bend

Published online by Cambridge University Press:  09 June 2017

Azan M. Sapardi ,
Wisam K. Hussam ,
Alban Pothérat  and
Gregory J. Sheard Open the ORCID record for Gregory J. Sheard [Opens in a new window]
Azan M. Sapardi
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia Department of Mechanical Engineering, International Islamic University Malaysia, Kuala Lumpur 53300, Malaysia
Wisam K. Hussam
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia School of Engineering, Australian College of Kuwait, Safat 13015, Kuwait
Alban Pothérat
Affiliation:
Applied Mathematics Research Centre, Coventry University, Coventry CV1 5FB, UK
Gregory J. Sheard*
Affiliation:
The Sheard Lab, Department of Mechanical and Aerospace Engineering, Monash University, Victoria 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study seeks to characterise the breakdown of the steady two-dimensional solution in the flow around a 180-degree sharp bend to infinitesimal three-dimensional disturbances using a linear stability analysis. The stability analysis predicts that three-dimensional transition is via a synchronous instability of the steady flows. A highly accurate global linear stability analysis of the flow was conducted with Reynolds number 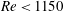$\mathit{Re}<1150$ and bend opening ratio (ratio of bend width to inlet height) 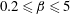$0.2\leqslant \unicode[STIX]{x1D6FD}\leqslant 5$. This range of 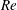$\mathit{Re}$ and 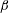$\unicode[STIX]{x1D6FD}$ captures both steady-state two-dimensional flow solutions and the inception of unsteady two-dimensional flow. For 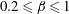$0.2\leqslant \unicode[STIX]{x1D6FD}\leqslant 1$, the two-dimensional base flow transitions from steady to unsteady at higher Reynolds number as 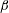$\unicode[STIX]{x1D6FD}$ increases. The stability analysis shows that at the onset of instability, the base flow becomes three-dimensionally unstable in two different modes, namely a spanwise oscillating mode for 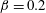$\unicode[STIX]{x1D6FD}=0.2$ and a spanwise synchronous mode for $\unicode[STIX]{x1D6FD}\geqslant 0.3$. The critical Reynolds number and the spanwise wavelength of perturbations increase as 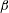$\unicode[STIX]{x1D6FD}$ increases. For 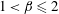$1<\unicode[STIX]{x1D6FD}\leqslant 2$ both the critical Reynolds number for onset of unsteadiness and the spanwise wavelength decrease as 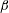$\unicode[STIX]{x1D6FD}$ increases. Finally, for 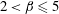$2<\unicode[STIX]{x1D6FD}\leqslant 5$, the critical Reynolds number and spanwise wavelength remain almost constant. The linear stability analysis also shows that the base flow becomes unstable to different three-dimensional modes depending on the opening ratio. The modes are found to be localised near the reattachment point of the first recirculation bubble.

JFM classification

Instability: Instability Wakes/Jets: Separated flows Waves/Free-surface Flows: Channel flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 813 - 847
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abu-Nada, E. 2008 Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step. Intl J. Heat Fluid Flow 29 (1), 242–249.Google Scholar
Alam, M. & Sandham, N. D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 403, 223–250.Google Scholar
Albarède, P. & Provansal, M. 1995 Quasi-periodic cylinder wakes and the Ginzburg–Landau equation. J. Fluid Mech. 291, 191–222.Google Scholar
Armaly, B. F., Durst, F., Pereira, J. C. F. & Schonung, B. 1983 Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 127, 473–496.CrossRefGoogle Scholar
Astarita, T. & Cardone, G. 2000 Thermofluidynamic analysis of the flow in a sharp 180° turn channel. Exp. Therm. Fluid Sci. 20 (3–4), 188–200.Google Scholar
Barkley, D., Blackburn, H. M. & Sherwin, S. J 2008 Direct optimal growth analysis for timesteppers. Intl J. Numer. Meth. Fluids 57 (9), 1435–1458.Google Scholar
Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–242.Google Scholar
Barleon, L., Casal, V. & Lenhart, L. 1991 MHD flow in liquid–metal-cooled blankets. Fusion Engng Des. 14 (3), 401–412.Google Scholar
Barleon, L., Mack, K. J. & Stieglitz, R. 1996 The MEKKA-facility: A Flexible Tool to Investigate MHD-flow Phenomena. Forschungszentrum Karlsruhe.Google Scholar
Barton, I. E. 1997 The entrance effect of laminar flow over a backward-facing step geometry. Intl J. Numer. Meth. Fluids 25 (6), 633–644.Google Scholar
Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.Google Scholar
Boccaccini, L. V., Giancarli, L., Janeschitz, G., Hermsmeyer, S., Poitevin, Y., Cardella, A. & Diegele, E. 2004 Materials and design of the European DEMO blankets. J. Nucl. Mater. 329, 148–155.Google Scholar
Brede, M., Eckelmann, H. & Rockwell, D. 1996 On secondary vortices in the cylinder wake. Phys. Fluids 8 (8), 2117–2124.Google Scholar
Bühler, L. 2007 Liquid metal magnetohydrodynamics for fusion blankets. In Magnetohydrodynamics: Historical Evolution and Trends (ed. Molokov, S., Moreau, R. & Moffatt, H. K.), Fluid Mechanics and its Applications, vol. 80, pp. 171–194. Springer.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the ow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.Google Scholar
Chung, Y. M., Tucker, P. G. & Roychowdhury, D. G. 2003 Unsteady laminar flow and convective heat transfer in a sharp 180° bend. Intl J. Heat Fluid Flow 24 (1), 67–76.Google Scholar
Cruchaga, M. A. 1998 A study of the backward-facing step problem using a generalized streamline formulation. Commun. Numer. Meth. Engng 14 (8), 697–708.3.0.CO;2-0>CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Duŝek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.Google Scholar
Erturk, E. 2008 Numerical solutions of 2-D steady incompressible flow over a backward-facing step. Part I: high Reynolds number solutions. Comput. Fluids 37 (6), 633–655.Google Scholar
Ghia, K. N., Osswald, G. A. & Ghia, U. 1989 Analysis of incompressible massively separated viscous flows using unsteady Navier–Stokes equations. Intl J. Numer. Meth. Fluids 9 (8), 1025–1050.CrossRefGoogle Scholar
Griffith, M. D., Leweke, T., Thompson, M. C. & Hourigan, K. 2008 Steady inlet flow in stenotic geometries: convective and absolute instabilities. J. Fluid Mech. 616, 111–133.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582 (1), 319–340.Google Scholar
Hammond, D. A. & Redekopp, L. G. 1998 Local and global instability properties of separation bubbles. Eur. J. Mech. (B/Fluids) 17 (2), 145–164.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Henderson, R. D. & Barkley, D. 1996 Secondary instability in the wake of a circular cylinder. Phys. Fluids 8, 1683.Google Scholar
Hirota, M., Fujita, H., Syuhada, A., Araki, S., Yoshida, T. & Tanaka, T. 1999 Heat/mass transfer characteristics in two-pass smooth channels with a sharp 180-deg turn. Intl J. Heat Mass Transfer 42 (20), 3757–3770.CrossRefGoogle Scholar
Hussam, W. K., Thompson, M. C. & Sheard, G. J. 2012a Enhancing heat transfer in a high Hartmann number magnetohydrodynamic channel flow via torsional oscillation of a cylindrical obstacle. Phys. Fluids 24 (11), 113601.CrossRefGoogle Scholar
Hussam, W. K., Thompson, M. C. & Sheard, G. J. 2012b Optimal transient disturbances behind a circular cylinder in a quasi-two-dimensional magnetohydrodynamic duct flow. Phys. Fluids 24 (2), 024105.Google Scholar
Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.Google Scholar
Kaiktsis, L., Karniadakis, G. E. & Orszag, S. A. 1991 Onset of three-dimensionality, equilibria, and early transition in flow over a backward-facing step. J. Fluid Mech. 231, 501–528.CrossRefGoogle Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kirillov, I. R., Reed, C. B., Barleon, L. & Miyazaki, K. 1995 Present understanding of MHD and heat transfer phenomena for liquid metal blankets. Fusion Engng Des. 27, 553–569.Google Scholar
Krall, K. M. & Sparrow, E. M. 1966 Turbulent heat transfer in the separated, reattached, and redevelopment regions of a circular tube. Trans. ASME J. Heat Transfer 88 (1), 131–136.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1976 Mechanics, p. 93. Pergamon.Google Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.Google Scholar
Larson, H. K. 1959 Heat transfer in separated flows. J. Aero. Sci. 26 (11), 731–738.Google Scholar
Le Gal, P., Nadim, A. & Thompson, M. 2001 Hysteresis in the forced Stuart–Landau equation: application to vortex shedding from an oscillating cylinder. J. Fluids Struct. 15 (3), 445–457.CrossRefGoogle Scholar
Lehoucq, R. B., Sorenson, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.Google Scholar
Liou, T.-M., Chen, C.-C., Tzeng, Y.-Y. & Tsai, T.-W. 2000 Non-intrusive measurements of near-wall fluid flow and surface heat transfer in a serpentine passage. Intl J. Heat Mass Transfer 43 (17), 3233–3244.Google Scholar
Liou, T.-M., Tzeng, Y.-Y. & Chen, C.-C. 1999 Fluid flow in a 180 deg sharp turning duct with different divider thicknesses. Trans. ASME J. Turbomach. 121 (3), 569–576.Google Scholar
Marquillie, M. & Ehrenstein, U. W. E. 2003 On the onset of nonlinear oscillations in a separating boundary-layer flow. J. Fluid Mech. 490, 169–188.Google Scholar
Metzger, D. E. & Sahm, M. K. 1986 Heat transfer around sharp 180-deg turns in smooth rectangular channels. Trans. ASME J. Heat Transfer 108 (3), 500–506.Google Scholar
Moffatt, H. K. 1985 Magnetostatic equilibria and analogous Euler flows of arbitrarily complex topology. Part 1. Fundamentals. J. Fluid Mech. 159, 359–378.Google Scholar
Mullin, T., Seddon, J. R. T., Mantle, M. D. & Sederman, A. J. 2009 Bifurcation phenomena in the flow through a sudden expansion in a circular pipe. Phys. Fluids 21 (1), 014110.Google Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Neild, A., Ng, T. W., Sheard, G. J., Powers, M. & Oberti, S. 2010 Swirl mixing at microfluidic junctions due to low frequency side channel fluidic perturbations. Sensors Actuators B 150 (2), 811–818.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
Ryan, K., Butler, C. J. & Sheard, G. J. 2012 Stability characteristics of a counter-rotating unequal strength Batchelor vortex pair. J. Fluid Mech. 696, 374–401.Google Scholar
Schumm, M., Berger, E. & Monkewitz, P. 1994 Self-excited oscillations in the wake of two-dimensional bluff bodies and their control. J. Fluid Mech. 271, 17–53.Google Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5), 734–742.Google Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 A coupled Landau model describing the Strouhal–Reynolds number profile of a three-dimensional circular cylinder wake. Phys. Fluids 15 (9), L68–L71.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004a Asymmetric structure and non-linear transition behaviour of the wakes of toroidal bodies. Eur. J. Mech. (B/Fluids) 23 (1), 167–179.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2004b From spheres to circular cylinders: non-axisymmetric transitions in the flow past rings. J. Fluid Mech. 506, 45–78.Google Scholar
Taneda, S. 1979 Visualization of separating Stokes flows. J. Phys. Soc. Japan 46, 1935–1942.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12 (2), 190–196.Google Scholar
Thompson, M. C. & Le Gal, P. 2004 The Stuart–Landau model applied to wake transition revisited. Eur. J. Mech. (B/Fluids) 23 (1), 219–228.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15 (3), 607–616.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.Google Scholar
Vo, T., Montabone, L. & Sheard, G. J. 2014 Linear stability analysis of a shear layer induced by differential coaxial rotation within a cylindrical enclosure. J. Fluid Mech. 738, 299–334.Google Scholar
Vo, T., Montabone, L. & Sheard, G. J. 2015 Effect of enclosure height on the structure and stability of shear layers induced by differential rotation. J. Fluid Mech. 765, 45–81.Google Scholar
Wang, T.-S. & Chyu, M. K. 1994 Heat convection in a 180-deg turning duct with different turn configurations. J. Thermophys. Heat Transfer 8 (3), 595–601.Google Scholar
Wee, D., Yi, T., Annaswamy, A. & Ghoniem, A. F. 2004 Self-sustained oscillations and vortex shedding in backward-facing step flows: simulation and linear instability analysis. Phys. Fluids 16 (9), 3361–3373.Google Scholar
Williamson, C. H. K. 1988 Defining a universal and continuous Strouhal–Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Phys. Fluids 31 (10), 2742–2744.Google Scholar
Zhang, L. & Pothérat, A. 2013 Influence of the geometry on the two- and three-dimensional dynamics of the flow in a 180° sharp bend. Phys. Fluids 25, 053605.Google Scholar