Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-21T14:33:35.941Z Has data issue: false hasContentIssue false
  • English
  • Français

The linear stability of an acceleration-skewed oscillatory Stokes layer

Published online by Cambridge University Press:  22 May 2020

Christian Thomas Open the ORCID record for Christian Thomas [Opens in a new window]
Christian Thomas*
Affiliation:
Department of Mathematics and Statistics, Macquarie University, NSW2109, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

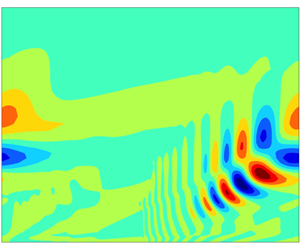
The linear stability of the family of flows generated by an acceleration-skewed oscillating planar wall is investigated using Floquet theory. Neutral stability curves and critical conditions for linear instability are determined for an extensive range of acceleration-skewed oscillating flows. Results indicate that acceleration skewness is destabilising and reduces the critical Reynolds number for the onset of linearly unstable behaviour. The structure of the eigenfunctions is discussed and solutions suggest that disturbances grow in the direction of highest acceleration.

JFM classification

Boundary Layers: Boundary layer stability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 895 , 25 July 2020 , A27
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van der A, D. A., O’Donoghue, T., Davies, A. G. & Ribberink, J. S. 2011 Experimental study of the turbulent boundary layer in acceleration-skewed oscillatory flow. J. Fluid Mech. 684, 251–283.CrossRefGoogle Scholar
Abreu, T., Silva, P. A., Sancho, F. & Temperville, A. 2010 Analytical approximate wave form for asymmetric waves. Coast. Engng 57, 656–667.CrossRefGoogle Scholar
Akhaven, R., Kamm, R. D. & Shapiro, A. H. 1991 An investigation of transition to turbulence in bounded oscillatory flows. Part 1. Experiments. J. Fluid Mech. 225, 395–422.CrossRefGoogle Scholar
Blennerhassett, P. J. & Bassom, A. P. 2002 The linear stability of flat Stokes layers. J. Fluid Mech. 464, 393–410.CrossRefGoogle Scholar
Blennerhassett, P. J. & Bassom, A. P. 2006 The linear stability of high-frequency oscillatory flow in a channel. J. Fluid Mech. 556, 1–25.CrossRefGoogle Scholar
Clamen, M. & Minton, P. 1977 An experimental investigation of flow in an oscillating pipe. J. Fluid Mech. 81, 421–431.CrossRefGoogle Scholar
Conrad, P. W. & Criminale, W. O. 1965 The stability of time-dependent laminar flow: parallel flows. Z. Angew. Math. Phys. 16, 233–254.CrossRefGoogle Scholar
Cowley, S. 1987 High frequency Rayleigh instability analysis of stokes layers. In Stability of Time-dependent and Spatially Varying Flows (ed. Dwoyer, D. L. & Hussaini, M. Y.), pp. 261–275. Springer.CrossRefGoogle Scholar
Davies, C. & Carpenter, P. 2001 A novel velocity-vorticity formulation of the Navier–Stokes equations with applications to boundary layer disturbance evolution. J. Comput. Phys. 172, 119–165.CrossRefGoogle Scholar
Davis, S. H. 1976 The stability of time-periodic flows. Annu. Rev. Fluid Mech. 8, 57–74.CrossRefGoogle Scholar
Dibajnia, M. & Watanabe, A. 1998 Transport rate under irregular sheet flow conditions. Coast. Engng 35, 167–183.CrossRefGoogle Scholar
Drake, T. G. & Calantoni, J. 2001 Discrete particle model for sheet flow sediment transport in the nearshore. J. Geophys. Res. 106 (C9), 19859–19868.CrossRefGoogle Scholar
Eckmann, D. M. & Grotberg, J. B. 1991 Experiments on transition to turbulence in oscillatory pipe flow. J. Fluid Mech. 222, 329–350.CrossRefGoogle Scholar
Elfrink, B., Hanes, D. M. & Ruussink, B. G. 2006 Parameterization and simulation of near bed orbital velocities under irregular waves in shallow water. Coast. Engng 53, 915–927.CrossRefGoogle Scholar
Fornberg, B. 1996 A Practical Guide to Pseudospectral Methods. Cambridge University Press.CrossRefGoogle Scholar
Hall, P. 1978 The linear stability of flat Stokes layers. Proc. R. Soc. Lond. A 359, 151–166.Google Scholar
Hall, P. 2003 On the stability of the Stokes layers at high Reynolds numbers. J. Fluid Mech. 482, 1–15.CrossRefGoogle Scholar
Hino, M., Sawamoto, M. & Takasu, S. 1976 Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech. 75, 193–207.CrossRefGoogle Scholar
Luo, J. & Wu, X. 2010 On the linear instability of a finite Stokes layer: instantaneous versus Floquet modes. Phys. Fluids 22, 054106.CrossRefGoogle Scholar
Madsen, O. 1974 Stability of a sand bed under breaking waves. In Proc. 14th Conf. on Coastal Engineering, Copenhagen, Denmark (ed. O’Brien, M. P.), pp. 776–794. ASCE.Google Scholar
Merkli, P. & Thomann, H. 1975 Transition to turbulence in oscillating pipe flow. J. Fluid Mech. 68, 567–575.CrossRefGoogle Scholar
Nielsen, P. & Callaghan, D. 2003 Shear stress and sediment transport calculations for sheet flow under waves. Coast. Engng 47, 347–354.CrossRefGoogle Scholar
O’Donoghue, T. & Wright, S. 2004 Concentrations in oscillatory sheet flow for well sorted and graded sands. Coast. Engng 50, 117–138.CrossRefGoogle Scholar
Ribberink, J. S. & Al-Salem, A. A. 1995 Sheet flow and suspension of sand in oscillatory boundary layers. Coast. Engng 25, 205–225.CrossRefGoogle Scholar
Scandura, P., Faraci, C. & Foti, E. 2016 A numerical investigation of acceleration-skewed oscillatory flows. J. Fluid Mech. 808, 576–613.CrossRefGoogle Scholar
Thomas, C., Bassom, A. P. & Blennerhassett, P. J. 2012 The linear stability of oscillating pipe flow. Phys. Fluids 24, 014105.CrossRefGoogle Scholar
Thomas, C., Bassom, A. P., Blennerhassett, P. J. & Davies, C. 2010 Direct numerical simulations of small disturbances in the classical Stokes layer. J. Engng Maths 68, 327–338.CrossRefGoogle Scholar
Thomas, C., Bassom, A. P., Blennerhassett, P. J. & Davies, C. 2011 The linear stability of oscillatory Poiseuille flow in channels and pipes. Proc. R. Soc. Lond. A 467, 2643–2662.CrossRefGoogle Scholar
Thomas, C., Blennerhassett, P. J., Bassom, A. P. & Davies, C. 2015 The linear stability of a Stokes layer subjected to high frequency perturbations. J. Fluid Mech. 764, 193–218.CrossRefGoogle Scholar
Thomas, C., Davies, C., Bassom, A. P. & Blennerhassett, P. J. 2014 Evolution of disturbance wavepackets in an oscillatory Stokes layer. J. Fluid Mech. 752, 543–571.CrossRefGoogle Scholar
Trefethen, N. 2000 Spectral Methods in MATLAB. SIAM.CrossRefGoogle Scholar
Vittori, G. & Verzicco, R. 1998 Direct simulation of transition in an oscillatory boundary layer. J. Fluid Mech. 371, 207–232.CrossRefGoogle Scholar
Von Kerczek, C. & Davis, S. H. 1974 Linear stability theory of oscillatory Stokes layers. J. Fluid Mech. 62, 753–773.CrossRefGoogle Scholar
Watanabe, A. & Sato, S. 2004 A sheet-flow transport rate formula for asymmetric forward-leaning waves and currents. In Proc. 29th Coastal Engng Conf., Lisbon, Portugal (ed. Smith, J. M.), pp. 1703–1714. World Scientific.Google Scholar