Hostname: page-component-6bf8c574d5-9nwgx Total loading time: 0 Render date: 2025-02-17T23:24:54.629Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of a ferrofluid centred around a current-carrying wire

Published online by Cambridge University Press:  19 May 2022

S.H. Ferguson Briggs Open the ORCID record for S.H. Ferguson Briggs [Opens in a new window]  and
A.J. Mestel Open the ORCID record for A.J. Mestel [Opens in a new window]
S.H. Ferguson Briggs*
Affiliation:
Imperial College London, Exhibition Road, South Kensington, London, SW7 2BX
A.J. Mestel
Affiliation:
Imperial College London, Exhibition Road, South Kensington, London, SW7 2BX
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

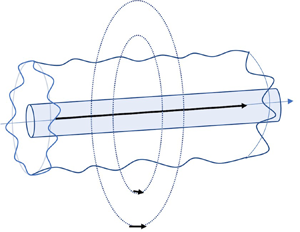
Investigated first is the linear stability of a Newtonian ferrofluid centred on a rigid wire, surrounded by another ferrofluid with a different magnetic susceptibility. An electric current runs through the wire, generating an azimuthal magnetic field that produces a magnetic stress at the interface of the fluids. Three-dimensional disturbances to the system are considered, and the linearised Navier–Stokes equations are solved analytically in terms of an implicit expression for the growth rate of the disturbance. The growth rate is found numerically for arbitrary Reynolds number, and given explicitly in the inviscid and Stokes regimes. Investigated next is a ferrofluid whose magnetic susceptibility varies radially, centred on a rigid wire, subject to a non-uniform azimuthal field. It is proven that if the gradient of the susceptibility is positive anywhere in the fluid, then the system is linearly unstable. Moreover, it is proven that applying an axial field can stabilise disturbances for both continuous and discontinuous susceptibilities.

JFM classification

MHD and Electrohydrodynamics: Magnetic fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 942 , 10 July 2022 , A20
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abdel Fattah, A.R., Ghosh, S. & Puri, I.K. 2016 Printing microstructures in a polymer matrix using a ferrofluid droplet. J. Magn. Magn. Mater. 401, 1054–1059.CrossRefGoogle Scholar
Arkhipenko, V.I., Barkov, Y.D., Bashtovoi, V.G. & Krakov, M.S. 1980 Investigation into the stability of a stationary cylindrical column of magnetizable liquid. Fluid Dyn. 15, 477–481.CrossRefGoogle Scholar
Asfer, M., Saroj, S.K. & Panigrahi, P.K. 2017 Retention of ferrofluid aggregates at the target site during magnetic drug targeting. J. Magn. Magn. Mater. 436, 47–55.CrossRefGoogle Scholar
Bashtovoi, V. & Krakov, M. 1978 Stability of an axisymmetric jet of magnetizable fluid. J. Appl. Mech. Tech. Phys. 19, 541–545.CrossRefGoogle Scholar
Blyth, M.G. & Parau, E.I. 2014 Solitary waves on a ferrofluid jet. J. Fluid Mech. 750, 401–420.CrossRefGoogle Scholar
Bourdin, E., Barci, J.-C. & Falcon, E. 2010 Observation of axisymmetric solitary waves on the surface of a ferrofluid. Am. Phys. Soc. 104, 094502.Google ScholarPubMed
Canu, R. & Renoult, M.-C. 2021 Linear stability analysis of a Newtonian ferrofluid cylinder surrounded by a Newtonian fluid. J. Fluid Mech. 927, A36.CrossRefGoogle Scholar
Charles, S.W. 1987 Some applications of magnetic fluids – use as an ink and in microwave systems. J. Magn. Magn. Mater. 65, 350–358.CrossRefGoogle Scholar
Christiansen, R.M. 1955 The influence of interfacial tension on the breakup of a liquid jet. PhD thesis, University of Pennsylvania, USA.Google Scholar
Cornish, M. 2018 Viscous and inviscid nonlinear dynamics of an axisymmetric ferrofluid jet. PhD thesis, Imperial College London.Google Scholar
Cowley, M.D. & Rosensweig, R.E. 1967 The interfacial stability of a ferromagnetic fluid. J. Fluid Mech. 30, 671–688.CrossRefGoogle Scholar
Doak, A. & Vanden-Broeck, J.-M. 2019 Travelling wave solutions on an axisymmetric ferrofluid jet. J. Fluid Mech. 865, 414–439.CrossRefGoogle Scholar
Garcia, F.J., Gonzz, H., Ramos, A. & Castellanos, A. 1997 Stability of insulating viscous jets under axial electric fields. J. Electrostat. 40, 41, 161–166.CrossRefGoogle Scholar
Gonella, V.C., Hanser, F., Vorwerk, J., Odenbach, S. & Baumgarten, D. 2020 Influence of local particle concentration gradient forces on the flow-mediated mass transport in a numerical model of magnetic drug targeting. J. Magn. Magn. Mater. 525, 167490.CrossRefGoogle Scholar
Korovin, V.M. 2004 Capillary disintegration of a configuration formed by two viscous ferrofluids surrounding a current-carrying conductor and having a cylindrical interface. Tech. Phys. 49, 669–676.CrossRefGoogle Scholar
Löwa, N., Fabert, J.-M., Gutkelch, D., Paysen, H., Kosch, O. & Wiekhorst, F. 2019 3D-printing of novel magnetic composites based on magnetic nanoparticles and photopolymers. J. Magn. Magn. Mater. 469, 456–460.CrossRefGoogle Scholar
Mestel, A.J. 1996 Electrohydrodynamic stability of a highly viscous jet. J. Fluid Mech. 312, 311–326.CrossRefGoogle Scholar
Nayyar, N.K & Murty, G.S. 1960 The stability of a dielectric liquid jet in the presence of a longitudinal electric field. Proc. Phys. Soc. Lond. 75, 369–373.CrossRefGoogle Scholar
Rannacher, D. & Engel, A. 2006 Cylindrical Korteweg–de Vries solitons on a ferrofluid surface. New J. Phys. 8, 108.CrossRefGoogle Scholar
Rayleigh, Lord 1878 On the instability of jets. Proc. Lond. Math. Soc. 10, 4–13.CrossRefGoogle Scholar
Rosensweig, R.E. 1985 Ferrohydrodynamics. Cambridge University Press.Google Scholar
Saville, D.A. 1971 Stability of electrically charged viscous cylinders. Phys. Fluids 14, 1095–1099.CrossRefGoogle Scholar
Scherer, C. & Figueiredo Neto, A.M. 2005 Ferrofluids: properties and applications. Braz. J. Phys. 35.CrossRefGoogle Scholar
Voltairas, P.A., Fotiadis, D.I. & Michalis, L.K. 2002 Hydrodynamics of magnetic drug targeting. J. Biomech. 35, 813–821.CrossRefGoogle ScholarPubMed
Zelazo, R.E. & Melcher, R.J. 1969 Dynamics and stability of ferrofluids: surface interactions. J. Fluid Mech. 39, 1–24.CrossRefGoogle Scholar
Zhang, L.-Y., Gu, H.-C. & Wang, X.-M. 2007 Magnetite ferrofluid with high specific absorption rate for application in hyperthermia. J. Magn. Magn. Mater. 311, 228–233.CrossRefGoogle Scholar