Article contents
Linear stability and energetics of rotating radial horizontal convection
Published online by Cambridge University Press: 13 April 2016
Abstract
The effect of rotation on horizontal convection in a cylindrical enclosure is investigated numerically. The thermal forcing is applied radially on the bottom boundary from the coincident axes of rotation and geometric symmetry of the enclosure. First, a spectral element method is used to obtain axisymmetric basic flow solutions to the time-dependent incompressible Navier–Stokes equations coupled via a Boussinesq approximation to a thermal transport equation for temperature. Solutions are obtained primarily at Rayleigh number 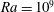 $\mathit{Ra}=10^{9}$ and rotation parameters up to
$\mathit{Ra}=10^{9}$ and rotation parameters up to 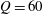 $Q=60$ (where
$Q=60$ (where 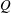 $Q$ is a non-dimensional ratio between thermal boundary layer thickness and Ekman layer depth) at a fixed Prandtl number
$Q$ is a non-dimensional ratio between thermal boundary layer thickness and Ekman layer depth) at a fixed Prandtl number 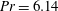 $\mathit{Pr}=6.14$ representative of water and enclosure height-to-radius ratio
$\mathit{Pr}=6.14$ representative of water and enclosure height-to-radius ratio 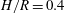 $H/R=0.4$. The axisymmetric solutions are consistently steady state at these parameters, and transition from a regime unaffected by rotation to an intermediate regime occurs at
$H/R=0.4$. The axisymmetric solutions are consistently steady state at these parameters, and transition from a regime unaffected by rotation to an intermediate regime occurs at 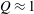 $Q\approx 1$ in which variation in thermal boundary layer thickness and Nusselt number are shown to be governed by a scaling proposed by Stern (1975, Ocean Circulation Physics. Academic). In this regime an increase in
$Q\approx 1$ in which variation in thermal boundary layer thickness and Nusselt number are shown to be governed by a scaling proposed by Stern (1975, Ocean Circulation Physics. Academic). In this regime an increase in 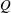 $Q$ sees the flow accumulate available potential energy and more strongly satisfy an inviscid change in potential energy criterion for baroclinic instability. At the strongest
$Q$ sees the flow accumulate available potential energy and more strongly satisfy an inviscid change in potential energy criterion for baroclinic instability. At the strongest 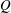 $Q$ the flow is dominated by rotation, accumulation of available potential energy ceases and horizontal convection is suppressed. A linear stability analysis reveals several instability mode branches, with dominant wavenumbers typically scaling with
$Q$ the flow is dominated by rotation, accumulation of available potential energy ceases and horizontal convection is suppressed. A linear stability analysis reveals several instability mode branches, with dominant wavenumbers typically scaling with 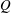 $Q$. Analysis of contributing terms of an azimuthally averaged perturbation kinetic energy equation applied to instability eigenmodes reveals that energy production by shear in the axisymmetric mean flow is negligible relative to that produced by conversion of available potential energy from the mean flow. An evolution equation for the quantity that facilitates this exchange, the vertical advective buoyancy flux, reveals that a baroclinic instability mechanism dominates over
$Q$. Analysis of contributing terms of an azimuthally averaged perturbation kinetic energy equation applied to instability eigenmodes reveals that energy production by shear in the axisymmetric mean flow is negligible relative to that produced by conversion of available potential energy from the mean flow. An evolution equation for the quantity that facilitates this exchange, the vertical advective buoyancy flux, reveals that a baroclinic instability mechanism dominates over 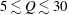 $5\lesssim Q\lesssim 30$, whereas stronger and weaker rotations are destabilised by vertical thermal gradients in the mean flow.
$5\lesssim Q\lesssim 30$, whereas stronger and weaker rotations are destabilised by vertical thermal gradients in the mean flow.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 16
- Cited by



