Published online by Cambridge University Press: 29 September 2021
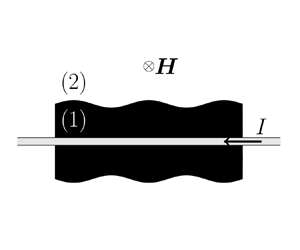
We performed a linear stability analysis of a Newtonian ferrofluid cylinder surrounded by a Newtonian non-magnetic fluid in an azimuthal magnetic field. A wire is used at the centre of the ferrofluid cylinder to create this magnetic field. Isothermal conditions are considered and gravity is ignored. An axisymmetric perturbation is imposed at the interface between the two fluids and a dispersion relation is obtained allowing us to predict whether the flow is stable or unstable with respect to this perturbation. This relation is dependent on the Ohnesorge number of the ferrofluid, the dynamic viscosity ratio, the density ratio, the magnetic Bond number, the relative magnetic permeability and the dimensionless wire radius. Solutions to this dispersion relation are compared with experimental data from Arkhipenko et al. (Fluid Dyn., vol. 15, issue 4, 1981, pp. 477–481) and, more recently, Bourdin et al. (Phys. Rev. Lett., vol. 104, issue 9, 2010, 094502). A better agreement than the inviscid theory and the theory that only takes into account the viscosity of the ferrofluid is shown with the data of Arkhipenko et al. (Fluid Dyn., vol. 15, issue 4, 1981, pp. 477–481) and those of Bourdin et al. (Phys. Rev. Lett., vol. 104, issue 9, 2010, 094502) for small wavenumbers.