Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T14:54:45.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear instability and nonlinear flow states in a horizontal pipe flow under bottom heating and transverse magnetic field

Published online by Cambridge University Press:  14 December 2022

Jun Hu Open the ORCID record for Jun Hu [Opens in a new window] ,
Haoyang Wu  and
Baofang Song Open the ORCID record for Baofang Song [Opens in a new window]
Jun Hu*
Affiliation:
Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, P.O. Box 8009, Beijing 100088, PR China
Haoyang Wu
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, PR China
Baofang Song*
Affiliation:
Center for Applied Mathematics, Tianjin University, Tianjin 300072, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

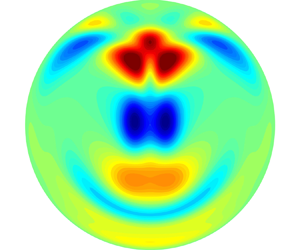
Linear stabilities of the liquid metal mixed convection in a horizontal pipe under bottom heating and transverse magnetic field are studied through linear global stability analyses. Three branches of the linear stability boundary curves are determined by the eigenvalue computation of the most unstable modes. One branch is located in the region of large Hartmann number and determined by the linear unstable mode which was first revealed by the numerical simulations of Zikanov, Listratov & Sviridov (J. Fluid Mech., vol. 720, 2013, pp. 486–516). This branch curve shows that the global unstable mode exists above a threshold of Hartmann number, which agrees with the experiment of Genin et al. (Temperature fluctuations in a heated horizontal tube affected by transverse magnetic field. In Proc. 8th PAMIR Conf. Fund. Appl. MHD, Borgo, Corsica, France, pp. 37–41, 2011). The other two branch curves determined by two different long-wave unstable modes intersect with each other in the region of small Hartmann number. The critical Grashof number on these two curves increases exponentially with the increase of the Hartmann number. Through energy budget analyses at the critical thresholds of these unstable modes, it is found that, for the unstable mode at large Hartmann numbers, buoyancy is the dominant destabilizing term which demonstrates the hypothetical explanation of Zikanov et al. (2013) who regard natural convection as a destabilization mechanism. It is further revealed that, with respect to the unstable modes on the critical stability curves of small Hartmann numbers, the dominant destabilization comes from the streamwise shear of the basic flow. Finally, within the linear unstable region, fully developed nonlinear flow states of the mixed convection are investigated by direct numerical simulations (DNS) with several sets of selected dimensionless parameters. The spatio-temporal structures of these nonlinear flow states are discussed in detail with comparison with the linear unstable global modes.

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A33
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abdou, M., Morley, N.B., Smolentsev, S., Ying, A., Malang, S., Rowcliffe, A. & Ulrickson, M. 2015 Blanket/first wall challenges and required R&D on the pathway to DEMO. Fusion Engng Des. 100, 2–43.CrossRefGoogle Scholar
Belyaev, I.A., Ivochkin, Y.P., Listratov, Y.I., Razuvanov, N.G. & Sviridov, V.G. 2015 Temperature fluctuations in a liquid metal MHD-flow in a horizontal inhomogeneously heated tube. High Temp. 53 (5), 734–741.CrossRefGoogle Scholar
Belyaev, I., Krasnov, D., Kolesnikov, Y., Biryukov, D., Chernysh, D., Zikanov, O. & Listratov, Y. 2020 Effects of symmetry on magnetohydrodynamic mixed convection flow in a vertical duct. Phys. Fluids 32, 094106.CrossRefGoogle Scholar
Belyaev, I., Sardov, P., Melnikov, I. & Frick, P. 2021 Limits of strong magneto-convective fluctuations in liquid metal flow in a heated vertical pipe affected by a transverse magnetic field. Intl J. Therm. Sci. 161, 106773.CrossRefGoogle Scholar
Davidson, P.A. 1995 Magnetic damping of jets and vortices. J. Fluid Mech. 299, 153–186.CrossRefGoogle Scholar
Davidson, P.A. 2001 An introduction to magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Forest, L., et al. 2020 Status of the EU DEMO breeding blanket manufacturing R&D activities. Fusion Engng Des. 152, 111420.CrossRefGoogle Scholar
Genin, L.G., Zhilin, V.G., Ivochkin, Y.P., Razuvanov, N.G., Belyaev, I.A., Listratov, Y.I. & Sviridov, V.G. 2011 Temperature fluctuations in a heated horizontal tube affected by transverse magnetic field. In Proc. 8th PAMIR Conf. Fund. Appl. MHD, Borgo, Corsica, France, pp. 37–41.Google Scholar
Hu, J. 2020 Linear global stability of liquid metal mixed convection in a horizontal bottom-heating duct under strong transverse magnetic field. Phys. Fluids 32, 034108.Google Scholar
Hu, J. 2021 Linear global stability of a downward flow of liquid metal in a vertical duct under strong wall heating and transverse magnetic field. Phys. Rev. Fluids 6, 073502.CrossRefGoogle Scholar
Hugues, S. & Randriamampianina, A. 1998 An improved projection scheme applied to pseudospectral methods for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 28, 501–521.3.0.CO;2-S>CrossRefGoogle Scholar
Hunt, J.C.R. 1965 Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 21, 577–590.CrossRefGoogle Scholar
Kakutani, T. 1964 The hydrodynamic stability of the modified plane Couette flow in the presence of a transverse magnetic field. J. Phys. Soc. Japan 19, 1041–1057.CrossRefGoogle Scholar
Kinet, M., Knaepen, B. & Molokov, S. 2009 Instabilities and transition in magnetohydrodynamic flows in ducts with electrically conducting walls. Phys. Rev. Lett. 103, 154501.CrossRefGoogle ScholarPubMed
Kirillov, I.R., Obukhov, D.M., Genin, L.G., Sviridov, V.G., Razuvanov, N.G., Batenin, V.M., Belyaev, I.A., Poddubnyi, I.I. & Yu Pyatnitskaya, N. 2016 Buoyancy effects in vertical rectangular duct with coplanar magnetic field and single sided heat load. Fusion Engng Des. 104, 1–8.CrossRefGoogle Scholar
Lehnert, B. 1952 On the behaviour of an electrically conductive liquid in a magnetic field. Ark. Fys. 5, 69–90.Google Scholar
Lehoucq, R., Sorensen, D. & Yang, C. 1998 Arpack users’ guide: Solution of large-scale eigenvalue problems with implicitly restarted arnoldi methods. SIAM.CrossRefGoogle Scholar
Ling, Q. & Wang, G. 2020 A research and development review of water-cooled breeding blanket for fusion reactors. Ann. Nucl. Energy 145, 107541.CrossRefGoogle Scholar
Listratov, Y., Melnikov, I., Razuvanov, N., Sviridov, V. & Zikanov, O. 2016 Convection instability and temperature fluctuations in a downward flow in a vertical pipe with strong transverse magnetic field. In Proceedings of 10th PAMIR Conference Fundamental and Applied MHD, Cagliari, Italy, vol. 1. INP, pp. 112–116. Open Library.Google Scholar
Liu, L. & Zikanov, O. 2015 Elevator mode convection in flows with strong magnetic fields. Phys. Fluids 27 (4), 044103.CrossRefGoogle Scholar
Melnikov, I.A., Sviridov, E.V., Sviridov, V.G. & Razuvanov, N.G. 2014 Heat transfer of MHD flow: Experimental and numerical research. In Proceedings of 9th PAMIR Conference Fundamental and Applied MHD, Riga Latvia, vol. 1. INP, pp. 65–69. Open Library.Google Scholar
Melnikov, I.A., Sviridov, E.V., Sviridov, V.G. & Razuvanov, N.G. 2016 Experimental investigation of MHD heat transfer in a vertical round tube affected by transverse magnetic field. Fusion Engng Des. 112, 505–512.CrossRefGoogle Scholar
Mistrangelo, C., Bühler, L., Smolentsev, S., Klüber, V., Maione, I. & Aubert, J. 2021 MHD flow in liquid metal blankets: major design issues, MHD guidelines and numerical analysis. Fusion Engng Des. 173, 112795.CrossRefGoogle Scholar
Moffatt, H.K. 1967 On the suppression of turbulence by a uniform magnetic field. J. Fluid Mech. 28 (3), 571–592.CrossRefGoogle Scholar
Molokov, S., Moreau, R. & Moffatt, H.K. 2007 Magnetohydrodynamics: Historical Evolution and Trends. Springer, Berlin.CrossRefGoogle Scholar
Moresco, P. & Alboussire, T. 2004 Experimental study of the instability of the Hartmann layer. J. Fluid Mech. 504, 167–181.CrossRefGoogle Scholar
Ni, M.-J., Munipalli, R., Morley, N.B., Huang, P. & Abdou, M.A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. J. Comput. Phys. 227, 174–204.CrossRefGoogle Scholar
Pironneau, O., Hecht, F. & Morice, J. 2013 Freefem++. Available at: http://www.freefem.org.Google Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2010 Linear stability of Hunt's flow. J. Fluid Mech. 649, 115–134.CrossRefGoogle Scholar
Priede, J., Aleksandrova, S. & Molokov, S. 2012 Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct. J. Fluid Mech. 708, 111–127.CrossRefGoogle Scholar
Priede, J., Arlt, T. & Bühler, L. 2015 Linear stability of magnetohydrodynamic flow in a square duct with thin conducting walls. J. Fluid Mech. 788, 129–146.CrossRefGoogle Scholar
Roberts, P.H. 1967 An Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Shatrov, V. & Gerbeth, G. 2010 Marginal turbulent magnetohydrodynamic flow in a square duct. Phys. Fluids 22 (8), 153–579.CrossRefGoogle Scholar
Smolentsev, S., Moreau, R., Bühler, L. & Mistrangelo, C. 2010 MHD thermofluid issues of liquid-metal blankets: phenomena and advances. Fusion Engng Des. 85, 1196–1205.CrossRefGoogle Scholar
Smolentsev, S., Morley, N.B., Abdou, M.A. & Malang, S. 2015 Dual- Coolant Lead–Lithium (DCLL) blanket status and R&D needs. Fusion Engng Des. 100, 44–54.CrossRefGoogle Scholar
Smolentsev, S., Vetcha, N. & Moreau, R. 2012 Study of instabilities and transitions for a family of quasi-two-dimensional magnetohydrodynamic flows based on a parametrical model. Phys. Fluids 24, 024101.CrossRefGoogle Scholar
Sommeria, J. & Moreau, R. 1982 Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.CrossRefGoogle Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
Vantieghem, S., Albets-Chico, X. & Knaepen, B. 2009 The velocity profile of laminar MHD flows in circular conducting pipes. Theor. Comput. Fluid Dyn. 23, 525–536.CrossRefGoogle Scholar
Vetcha, N., Smolentsev, S., Abdou, M. & Moreau, R. 2013 Study of instabilities and quasi-two-dimensional turbulence in volumetrically heated magnetohydrodynamic flows in a vertical rectangular duct. Phys. Fluids 25, 024102.CrossRefGoogle Scholar
Vo, T., Pothérat, A. & Sheard, G.J. 2017 Linear stability of horizontal, laminar fully developed, quasi-two-dimensional liquid metal duct flow under a transverse magnetic field and heated from below. Phys. Rev. Fluids 2, 033902.CrossRefGoogle Scholar
Willis, A.P. 2017 The Openpipeflow Navier–Stokes solver. Software X 6, 124–127.Google Scholar
Zhang, X. & Zikanov, O. 2014 Mixed convection in a horizontal duct with bottom heating and strong transverse magnetic field. J. Fluid Mech. 757, 33–56.CrossRefGoogle Scholar
Zhang, X. & Zikanov, O. 2018 Convection instability in a downward flow in a vertical duct with strong transverse magnetic field. Phys. Fluids 30, 117101.CrossRefGoogle Scholar
Zikanov, O., Belyaev, I., Listratov, Y., Frick, P., Razuvanov, N. & Sardov, P. 2021 Mixed convection in pipe and duct flows with strong magnetic fields. Appl. Mech. Rev. 73, 010801.CrossRefGoogle Scholar
Zikanov, O., Krasnov, D., Boeck, T., Thess, A. & Rossi, M. 2014 Laminar-turbulent transition in magnetohydrodynamic duct, pipe, and channel flows. Appl. Mech. Rev. 66, 030802.CrossRefGoogle Scholar
Zikanov, O. & Listratov, Y. 2016 Numerical investigation of MHD heat transfer in a vertical round tube affected by transverse magnetic field. Fusion Engng Des. 113, 151–161.CrossRefGoogle Scholar
Zikanov, O., Listratov, Y.I. & Sviridov, V.G. 2013 Natural convection in horizontal pipe flow with a strong transverse magnetic field. J. Fluid Mech. 720, 486–516.CrossRefGoogle Scholar