Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T04:40:32.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear global instability of non-orthogonal incompressible swept attachment-line boundary-layer flow

Published online by Cambridge University Press:  23 August 2012

José Miguel Pérez ,
Daniel Rodríguez  and
Vassilis Theofilis
José Miguel Pérez*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Plaza del Cardenal Cisneros 3, E-28040 Madrid, Spain
Daniel Rodríguez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Plaza del Cardenal Cisneros 3, E-28040 Madrid, Spain Engineering and Applied Sciences, California Institute of Technology, Pasadena, CA 91125, USA
Vassilis Theofilis
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, Plaza del Cardenal Cisneros 3, E-28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Flow instability in the non-orthogonal swept attachment-line boundary layer is addressed in a linear analysis framework via solution of the pertinent global (BiGlobal) partial differential equation (PDE)-based eigenvalue problem. Subsequently, a simple extension of the extended Görtler–Hämmerlin ordinary differential equation (ODE)-based polynomial model proposed by Theofilis et al. (2003) for orthogonal flow, which includes previous models as special cases and recovers global instability analysis results, is presented for non-orthogonal flow. Direct numerical simulations have been used to verify the analysis results and unravel the limits of validity of the basic flow model analysed. The effect of the angle of attack, 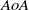, on the critical conditions of the non-orthogonal problem has been documented; an increase of the angle of attack, from 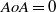(orthogonal flow) up to values close to 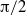which make the assumptions under which the basic flow is derived questionable, is found to systematically destabilize the flow. The critical conditions of non-orthogonal flows at 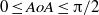are shown to be recoverable from those of orthogonal flow, via a simple algebraic transformation involving .

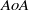Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 131 - 153
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Amestoy, P. R., Duff, I. S., L’Excellent, J.-Y. & Koster, J. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applics 1, 15–41.CrossRefGoogle Scholar
2. Bertolotti, F. P. 1999 On the connection between cross-flow vortices and attachment-line instabilities. In Proc. of the IUTAM Laminar-Turbulent Symposium V (ed. W. Saric & H. Fasel), pp. 625–630, Sedona.CrossRefGoogle Scholar
3. Brattkus, K. & Davis, S. H. 1991 The linear stability of plane stagnation-point flow against general disturbances. Q. J. Mech. Appl. Maths 44 (2), 135–146.CrossRefGoogle Scholar
4. Collis, S. & Lele, S. 1999 Receptivity to surface roughness near a swept leading edge. J. Fluid Mech. 380, 141–168.CrossRefGoogle Scholar
5. Criminale, W. O., Jackson, T. L. & Lasseigne, D. G. 1994 Evolution of disturbances in stagnation-point flow. J. Fluid Mech. 270, 331–347.CrossRefGoogle Scholar
6. Crouch, J. D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 224 (2), 924–940.CrossRefGoogle Scholar
7. Dorrepaal, J. M. 1986 An exact solution of the Navier–Stokes equations which describes non-orthogonal stagnation-point flow in two dimensions. J. Fluid Mech. 163, 141–147.CrossRefGoogle Scholar
8. Floryan, J. 1992 Stability of plane nonorthogonal stagnation flow. AIAA J. 30 (6), 1659–1662.CrossRefGoogle Scholar
9. Floryan, J. M. & Dallmann, U. C. 1990 Flow over a leading edge with distributed roughness. J. Fluid Mech. 216, 629–656.CrossRefGoogle Scholar
10. Gaster, M. 1967 On the flow along swept leading edges. Aero. Q. 18, 165–184.CrossRefGoogle Scholar
11. Görtler, H. 1955 Dreidimensionale Instabilität der ebenen Staupunktströmung gegenüber wirbelartigen Störungen. In 50 Jahre Grenzschichtforschung (ed. Görtler, H. & Tollmien, W. ). pp. 304–314. Vieweg und Sohn.CrossRefGoogle Scholar
12. Gray, W. E. 1952 The effect of wing sweep on laminar flow. Royal Aircraft Establishment, RAE TM 255 (ARC 14, 929).Google Scholar
13. Guégan, A., Schmid, P. J. & Huerre, P. 2008 Spatial optimal disturbances in swept attachment-line boundary layers. J. Fluid Mech. 603, 179–188.CrossRefGoogle Scholar
14. Hall, P., Malik, M. R. & Poll, D. I. A. 1984 On the stability of an infinitive swept attachment line boundary layer. Proc. R. Soc. Lond. A 395, 229–245.Google Scholar
15. Hämmerlin, H. 1955 Zur Instabilitätstheorie der ebenen Staupunktströmung. In 50 jahre grenzschichtforschung, pp. 315–327. Vieweg und Sohn.CrossRefGoogle Scholar
16. Hiemenz, K. 1911 Die Grenzschicht an einem in den gleichförmigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder. Dingl. Polytechn. J. 326, 321–324, thesis, Göttingen.Google Scholar
17. Joslin, R. D. 1996 Simulation of nonlinear instabilities in an attachment-line boundary layer. Fluid Dyn. Res. 18 (2), 81–97.CrossRefGoogle Scholar
18. Lasseigne, D. G. & Jackson, T. L. 1992 Stability of a non-orthogonal stagnation flow for three-dimensional disturbances. Theor. Comput. Fluid Dyn. 3, 207–218.CrossRefGoogle Scholar
19. Lasseigne, D. G., Jackson, T. L. & Hu, F. Q. 1992 Temperature and suction effects on the instability of an infinite swept attachment line. Phys. Fluids A 4 (9), 2008–2012.CrossRefGoogle Scholar
20. Lin, R. S. & Malik, M. R. 1996 On the stability of attachment-line boundary layers. Part 1. The incompressible swept Hiemenz flow. J. Fluid Mech. 311, 239–255.CrossRefGoogle Scholar
21. Lin, R. S. & Malik, M. R. 1997 On the stability of attachment-line boundary layers. Part 2. The effect of leading-edge curvature. J. Fluid Mech. 333, 125–137.CrossRefGoogle Scholar
22. Lundbladh, A., Schmid, P., Berlin, S. & Henningson, D. 1994 Simulation of by-pass transition in spatially evolving flow. In Proceedings of the AGARD Symposium on Application of Direct and Large Eddy Simulation to Transition and Turbulence, no. CP-551 in AGARD, pp. 18.1–18.13.Google Scholar
23. Lyell, M. J. & Huerre, P. 1985 Linear and nonlinear stability of plane stagnation flow. J. Fluid Mech. 161, 295–312.CrossRefGoogle Scholar
24. Mack, C. J. & Schmid, P. J. 2010 Direct numerical study of hypersonic flow about a swept parabolic body. Comput. Fluids 39 (10), 1932–1943.CrossRefGoogle Scholar
25. Mack, C. J., Schmid, P. J. & Sesterhenn, J. 2008 Global stability of swept flow around a parabolic body: connecting attachment-line and crossflow modes. J. Fluid Mech. 611, 205–214.CrossRefGoogle Scholar
26. Obrist, D. 2000 On the stability of the swept leading-edge boundary layer. PhD thesis, University of Washington.Google Scholar
27. Obrist, D. & Schmid, P. J. 2003 On the linear stability of swept attachment-line boundary layer flow. Part 2. Non-modal effects and receptivity. J. Fluid Mech. 493, 31–58.CrossRefGoogle Scholar
28. Pérez, J. M. 2012 Efficient numerical methods for global linear instability. Analysis and modeling of non-orthogonal swept attachment-line boundary layer flow. PhD thesis, School of Aeronautics, Technical University of Madrid.Google Scholar
29. Pfenninger, W. & Bacon, J. 1969 Amplified Laminar Boundary Layer Oscillation and Transition at the Attachment Line of a 45∘ Swept Flat-nosed Wing with and without Suction. Plenum.CrossRefGoogle Scholar
30. Poll, D. I. A. 1979 Transition in the infinite swept attachment line boundary layer. Aero. Q. 30, 607–629.CrossRefGoogle Scholar
31. Rodríguez, D. & Theofilis, V. 2010 Structural changes of laminar separation bubbles induced by global linear instability. J. Fluid Mech. 655, 280–305.CrossRefGoogle Scholar
32. Rosenhead, L. 1963 Laminar Boundary Layers. Oxford University Press.Google Scholar
33. Schlichting, H. 1979 Boundary Layer Theory, 7th edn. McGraw-Hill.Google Scholar
34. Spalart, P. R. 1988 Direct numerical study of leading-edge contamination. AGARD-CP-438 5, 1–13.Google Scholar
35. Stuart, J. T. 1959 The viscous flow near a stagnation point when the external flow has uniform vorticity. J. Aero/Space Sci. 26, 124–125.CrossRefGoogle Scholar
36. Sutera, S. P. 1965 Vorticity amplification in stagnation point flow and its effects on heat transfer. J. Fluid Mech. 21 (3), 513–534.CrossRefGoogle Scholar
37. Tamada, K. 1979 Two-dimensional stagnation-point flow impinging obliquely on a plane wall. J. Phys. Soc. Japan 46, 310–311.CrossRefGoogle Scholar
38. Theofilis, V. 1993 Numerical experiments on the stability of leading edge boundary layer flow: a two-dimensional linear study. Intl J. Numer. Meth. Fluids 16, 153–170.CrossRefGoogle Scholar
39. Theofilis, V. 1995 Spatial stability of incompressible attachment-line flow. Theor. Comp. Fluid Dyn. 7 (3), 159–171.CrossRefGoogle Scholar
40. Theofilis, V. 2003 Advances in global linear instability of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.CrossRefGoogle Scholar
41. Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.CrossRefGoogle Scholar
42. Theofilis, V., Fedorov, A. & Collis, S. 2006 Leading-edge boundary layer flow (Prandtl’s vision, current developments and future perspectives). In IUTAM Symposium on One Hundred Years of Boundary Layer Research 129, 73–82.Google Scholar
43. Theofilis, V., Fedorov, A., Obrist, D. & Dallmann, U. C. 2003 The extended Görtler–Hämmerlin model for linear instability of three-dimensional incompressible swept attachment-line boundary layer flow. J. Fluid Mech. 487, 271–313.CrossRefGoogle Scholar
44. Wilson, S. & Gladwell, I. 1978 The stability of a two-dimensional stagnation flow to three-dimensional disturbances. J. Fluid Mech. 84, 517–527.CrossRefGoogle Scholar
45. Xiong, Z. & Lele, S. 2007 Stagnation-point flow under free stream turbulence. J. Fluid Mech. 590, 1–33.CrossRefGoogle Scholar