Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T21:03:17.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear and nonlinear sensor placement strategies for mean-flow reconstruction via data assimilation

Published online by Cambridge University Press:  21 July 2021

Vincent Mons Open the ORCID record for Vincent Mons [Opens in a new window]  and
Olivier Marquet Open the ORCID record for Olivier Marquet [Opens in a new window]
Vincent Mons*
Affiliation:
DAAA, ONERA, Université Paris Saclay, F-92190Meudon, France
Olivier Marquet
Affiliation:
DAAA, ONERA, Université Paris Saclay, F-92190Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

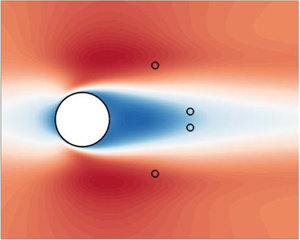
Reynolds-averaged Navier–Stokes (RANS)-based data assimilation has proven to be essential in many data-driven approaches, including the augmentation of experimental data and the identification of turbulence model corrections. As dense measurements of the whole mean flow are not always available when performing data assimilation, we here investigate the case where only a few punctual mean velocity measurements are employed to infer the full mean flow. Sensor placement methodologies are developed targeting an enhancement in either (i) the extrapolation of the full mean velocity field from the few punctual measurements or (ii) the identification of the considered model correction, which is here a forcing term in the momentum equations that accounts for the divergence of the Reynolds stress tensor. Concerning the first objective, a sensor placement procedure based on the correct reconstruction of the dominant singular modes of the linearized RANS equations is developed. When focusing on retrieving the model correction, we propose in particular a second-order adjoint-based approach to improve the well posedness of the data assimilation problem. It consists in minimizing the condition number of the Hessian operator that is associated with the cost function to optimize in data assimilation. This procedure allows us to take into account all nonlinearities in the present inverse problem during the optimization of the sensor locations, thus ensuring its effectiveness. Numerical experiments on the reconstruction of the mean flow around a circular cylinder at $Re=150$ confirm the validity of the developed sensor placement methodologies, which enable a significant improvement in the fidelity of the reconstructed flow with respect to the true one in multiple scenarios in terms of number of sensors and initial network arrangements.

JFM classification

Mathematical Foundations: Variational methods Wakes/Jets: Wakes Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 923 , 25 September 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akhtar, I., Borggaard, J., Burns, J.A., Imtiaz, H. & Zietsman, L. 2015 Using functional gains for effective sensor location in flow control: a reduced-order modelling approach. J. Fluid Mech. 781, 622–656.CrossRefGoogle Scholar
Alekseev, A.K. & Navon, I.M. 2001 The analysis of an ill-posed problem using multi-scale resolution and second-order adjoint techniques. Comput. Meth. Appl. Mech. Engng 190, 1937–1953.CrossRefGoogle Scholar
Armijo, L. 1966 Minimization of functions having Lipschitz continuous first partial derivatives. Pac. J. Maths 16, 1–3.CrossRefGoogle Scholar
Baker, N.L. & Daley, R. 2000 Observation and background adjoint sensitivity in the adaptive observation-targeting problem. Q. J. R. Meteorol. Soc. 126, 1431–1454.CrossRefGoogle Scholar
Belson, B.A., Semeraro, O., Rowley, C.W. & Henningson, D.S. 2013 Feedback control of instabilities in the two-dimensional Blasius boundary layer: the role of sensors and actuators. Phys. Fluids 25, 054106.CrossRefGoogle Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.CrossRefGoogle Scholar
Beneddine, S., Yegavian, R., Sipp, D. & Leclaire, B. 2017 Unsteady flow dynamics reconstruction from mean flow and point sensors: an experimental study. J. Fluid Mech. 824, 174–201.CrossRefGoogle Scholar
Buizza, R. & Montani, A. 1999 Targeting observations using singular vectors. J. Atmos. Sci. 56, 2965–2985.2.0.CO;2>CrossRefGoogle Scholar
Chandramouli, P., Mémin, E. & Heitz, D. 2020 4D large scale variational data assimilation of a turbulent flow with a dynamics error model. J. Comput. Phys. 412, 109446.CrossRefGoogle Scholar
Chen, K.K. & Rowley, C.W. 2011 $H_2$ optimal actuator and sensor placement in the linearised complex Ginzburg-Landau system. J. Fluid Mech. 681, 241–260.CrossRefGoogle Scholar
Cioaca, A. & Sandu, A. 2014 An optimization framework to improve 4D-Var data assimilation system performance. J. Comput. Phys. 275, 377–389.CrossRefGoogle Scholar
Cioaca, A., Sandu, A. & de Sturler, E. 2013 Efficient methods for computing observation impact in 4D-Var data assimilation. Comput. Geosci. 17, 975–990.CrossRefGoogle Scholar
Cohen, K., Siegel, S. & McLaughlin, T. 2006 A heuristic approach to effective sensor placement for modeling of a cylinder wake. Comput. Fluids 35, 103–120.CrossRefGoogle Scholar
Da Silva, A.F.C. & Colonius, T. 2020 Flow state estimation in the presence of discretization errors. J. Fluid Mech. 890, A10.CrossRefGoogle Scholar
Daescu, D.N. 2008 On the sensitivity equations of four-dimensional variational (4D-Var) data assimilation. Mon. Weath. Rev. 136, 3050–3065.CrossRefGoogle Scholar
Daescu, D.N. & Navon, I.M. 2004 Adaptive observations in the context of 4D-Var data assimilation. Meteorol. Atmos. Phys. 85, 205–226.CrossRefGoogle Scholar
Duraisamy, K., Iaccarino, G. & Xiao, H. 2019 Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 51, 357–377.CrossRefGoogle Scholar
Durbin, P.A. 2018 Some recent developments in turbulence closure modeling. Annu. Rev. Fluid Mech. 50, 77–103.CrossRefGoogle Scholar
Foures, D.P.G., Dovetta, N., Sipp, D. & Schmid, P.J. 2014 A data-assimilation method for Reynolds-averaged Navier–Stokes-driven mean flow reconstruction. J. Fluid Mech. 759, 404–431.CrossRefGoogle Scholar
Franceschini, L., Sipp, D. & Marquet, O. 2020 Mean-flow data assimilation based on minimal correction of turbulence models: application to turbulent high-Reynolds number backward-facing step. Phys. Rev. Fluids 5, 094603.CrossRefGoogle Scholar
Gejadze, I.Y. & Shutyaev, V. 2012 On computation of the design function gradient for the sensor-location problem in variational data assimilation. SIAM J. Sci. Comput. 34, B127–B147.CrossRefGoogle Scholar
Gejadze, I.Y., Shutyaev, V.P. & Le Dimet, F.-X. 2018 Hessian-based covariance approximations in variational data assimilation. Russ. J. Numer. Anal. Math. Model. 33, 25–39.CrossRefGoogle Scholar
Gillissen, J.J.J., Bouffanais, R. & Yue, D.K.P. 2019 Data assimilation method to de-noise and de-filter particle image velocimetry data. J. Fluid Mech. 877, 196–213.CrossRefGoogle Scholar
Godinez, H.C. & Daescu, D.N. 2011 Observation targeting with a second-order adjoint method for increased predictability. Comput. Geosci. 15, 477–488.CrossRefGoogle Scholar
Hayase, T. 2015 Numerical simulation of real-world flows. Fluid Dyn. Res. 47, 051201.CrossRefGoogle Scholar
He, C., Liu, Y., Gan, L. & Lesshafft, L. 2019 Data assimilation and resolvent analysis of turbulent flow behind a wall-proximity rib. Phys. Fluids 31, 025118.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Math. 20, 251–265.CrossRefGoogle Scholar
Heitz, D., Mémin, E. & Schnörr, C. 2010 Variational fluid flow measurements from image sequences: synopsis and perspectives. Exp. Fluids 48, 369–393.CrossRefGoogle Scholar
Holland, J.R., Baeder, J.D. & Duraisamy, K. 2019 Field inversion and machine learning with embedded neural networks: physics-consistent neural network training. AIAA Paper 2019-3200.CrossRefGoogle Scholar
Hossen, M.J., Navon, I.M. & Daescu, D.N. 2012 Effect of random perturbations on adaptive observation techniques. Intl J. Numer. Meth. Fluids 69, 110–123.CrossRefGoogle Scholar
Juillet, F., Schmid, P.J. & Huerre, P. 2013 Control of amplifier flows using subspace identification techniques. J. Fluid Mech. 725, 522–565.CrossRefGoogle Scholar
Kang, W. & Xu, L. 2012 Optimal placement of mobile sensors for data assimilations. Tellus A 64, 17133.CrossRefGoogle Scholar
Kato, H., Yoshizawa, A., Ueno, G. & Obayashi, S. 2015 A data assimilation methodology for reconstructing turbulent flows around aircraft. J. Comput. Phys. 283, 559–581.CrossRefGoogle Scholar
Langland, R.H. & Baker, N.L. 2004 Estimation of observation impact using the NRL atmospheric variational data assimilation adjoint system. Tellus A 56, 189–201.CrossRefGoogle Scholar
Le Dimet, F.-X., Navon, I.M. & Daescu, D.N. 2002 Second-order information in data assimilation. Mon. Weath. Rev. 130, 629–648.2.0.CO;2>CrossRefGoogle Scholar
Le Dimet, F.-X., Ngodock, H.-E., Luong, B. & Verron, J. 1997 Sensitivity analysis in variational data assimilation. J. Meteorol. Soc. Japan 75, 245–255.CrossRefGoogle Scholar
Le Dimet, F.-X. & Talagrand, O. 1986 Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects. Tellus A 38A, 97–110.CrossRefGoogle Scholar
Lewis, J.M., Lakshmivarahan, S. & Dhall, S.K. 2006 Dynamic Data Assimilation: A Least Squares Approach, Encyclopedia of Mathematics and its Applications, vol. 104. Cambridge University Press.CrossRefGoogle Scholar
Li, Y., Zhang, J., Dong, G. & Abdullah, N.S. 2020 Small-scale reconstruction in three-dimensional Kolmogorov flows using four-dimensional variational data assimilation. J. Fluid Mech. 885, A9.CrossRefGoogle Scholar
Manohar, K., Brunton, B.W., Kutz, J.N. & Brunton, S.L. 2018 Data-driven sparse sensor placement for reconstruction: demonstrating the benefits of exploiting known patterns. IEEE Cont. Syst. Mag. 38, 63–86.Google Scholar
McKeon, B.J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.CrossRefGoogle Scholar
Meldi, M. & Poux, A. 2017 A reduced order model based on Kalman filtering for sequential data assimilation of turbulent flows. J. Comput. Phys. 347, 207–234.CrossRefGoogle Scholar
Mokhasi, P. & Rempfer, D. 2004 Optimized sensor placement for urban flow measurement. Phys. Fluids 16, 1758–1764.CrossRefGoogle Scholar
Mons, V., Chassaing, J.-C. & Sagaut, P. 2017 Optimal sensor placement for variational data assimilation of unsteady flows past a rotationally oscillating cylinder. J. Fluid Mech. 823, 230–277.CrossRefGoogle Scholar
Mons, V., Wang, Q. & Zaki, T. 2019 Kriging-enhanced ensemble variational data assimilation for scalar-source identification in turbulent environments. J. Comput. Phys. 398, 108856.CrossRefGoogle Scholar
Nocedal, J. 1980 Updating quasi-Newton matrices with limited storage. Math. Comput. 35, 773–782.CrossRefGoogle Scholar
Oehler, S.F. & Illingworth, S.J. 2018 Sensor and actuator placement trade-offs for a linear model of spatially developing flows. J. Fluid Mech. 854, 34–55.CrossRefGoogle Scholar
Palmer, T.N., Gelaro, R., Barkmeijer, J. & Buizza, R. 1998 Singular vectors, metrics, and adaptive observations. J. Atmos. Sci. 55, 633–653.2.0.CO;2>CrossRefGoogle Scholar
Parish, E.J. & Duraisamy, K. 2016 A paradigm for data-driven predictive modeling using field inversion and machine learning. J. Comput. Phys. 305, 758–774.CrossRefGoogle Scholar
Peter, J.E.V. & Dwight, R.P. 2010 Numerical sensitivity analysis for aerodynamic optimization: a survey of approaches. Comput. Fluids 39, 373–391.CrossRefGoogle Scholar
Rabier, F., Klinker, E., Courtier, P. & Hollingsworth, A. 1996 Sensitivity of forecast errors to initial conditions. Q. J. R. Meteorol. Soc. 122, 121–150.CrossRefGoogle Scholar
Ranieri, J., Chebira, A. & Vetterli, M. 2014 Near-optimal sensor placement for linear inverse problems. IEEE Trans. Signal Process. 62, 1135–1146.CrossRefGoogle Scholar
Saad, Y. 2011 Numerical Methods for Large Eigenvalue Problems, revised edn. SIAM.CrossRefGoogle Scholar
Singh, A.P. & Duraisamy, K. 2016 Using field inversion to quantify functional errors in turbulence closures. Phys. Fluids 28, 045110.CrossRefGoogle Scholar
Suzuki, T. 2012 Reduced-order Kalman-filtered hybrid simulation combining particle tracking velocimetry and direct numerical simulation. J. Fluid Mech. 709, 249–288.CrossRefGoogle Scholar
Symon, S., Dovetta, N., McKeon, B.J., Sipp, D. & Schmid, P.J. 2017 Data assimilation of mean velocity from 2D PIV measurements of flow over an idealized airfoil. Exp. Fluids 58, 61.CrossRefGoogle Scholar
Symon, S., Sipp, D. & McKeon, B.J. 2019 A tale of two airfoils: resolvent-based modelling of an oscillator versus an amplifier from an experimental mean. J. Fluid Mech. 881, 51–83.CrossRefGoogle Scholar
Wang, Z., Navon, I.M., Le Dimet, F.-X. & Zou, X. 1992 The second order adjoint analysis: theory and applications. Meteorol. Atmos. Phys. 50, 3–20.CrossRefGoogle Scholar
Wikle, C.K. & Berliner, L.M. 2007 A Bayesian tutorial for data assimilation. Physica D 230, 1–16.CrossRefGoogle Scholar
Willcox, K. 2006 Unsteady flow sensing and estimation via the gappy proper orthogonal decomposition. Comput. Fluids 35, 208–226.CrossRefGoogle Scholar
Xiao, H. & Cinnella, P. 2019 Quantification of model uncertainty in RANS simulations: a review. Prog. Aerosp. Sci. 51, 1–31.CrossRefGoogle Scholar
Xiao, H., Wu, J.-L., Wang, J.-X., Sun, R. & Roy, C.J. 2016 Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier–Stokes simulations: a data-driven, physics-informed Bayesian approach. J. Comput. Phys. 324, 115–136.CrossRefGoogle Scholar
Yildirim, B., Chryssostomidis, C. & Karniadakis, G.E. 2009 Efficient sensor placement for ocean measurements using low-dimensional concepts. Ocean Model. 27, 160–173.CrossRefGoogle Scholar
Yoshimura, R., Yakeno, A., Misaka, T. & Obayashi, S. 2020 Application of observability Gramian to targeted observation in WRF data assimilation. Tellus A 72, 1–11.CrossRefGoogle Scholar