1. Introduction
The recent rise of renewable energy sources is promoting the use of hydrogen as a carbon-free energy carrier (Perner & Bothe Reference Perner and Bothe2018). One possibility to harness the energy stored in hydrogen is its use in thermochemical energy conversion processes such as in gas turbines, industrial burners or piston engines (Sartbaeva et al. Reference Sartbaeva, Kuznetsov, Wells and Edwards2008). However, lean premixed hydrogen/air flames are prone to intrinsic combustion instabilities and, in particular, thermodiffusive instabilities, which can substantially change flame dynamics, heat release rates and flame speeds (Kadowaki & Hasegawa Reference Kadowaki and Hasegawa2005; Yuan, Ju & Law Reference Yuan, Ju and Law2007; Altantzis et al. Reference Altantzis, Frouzakis, Tomboulides, Kerkemeier and Boulouchos2011; Frouzakis et al. Reference Frouzakis, Fogla, Tomboulides, Altantzis and Matalon2015; Yu et al. Reference Yu, Yu, Bai, Sun and Tan2017; Fernández-Galisteo, Kurdyumov & Ronney Reference Fernández-Galisteo, Kurdyumov and Ronney2018; Berger et al. Reference Berger, Kleinheinz, Attili and Pitsch2019; Berger, Attili & Pitsch Reference Berger, Attili and Pitsch2022b). Thermodiffusive instabilities originate from the low Lewis number of hydrogen, which represents the ratio of the thermal and mass diffusivity, where the latter is particularly high for hydrogen (Sivashinsky Reference Sivashinsky1983; Matalon, Cui & Bechtold Reference Matalon, Cui and Bechtold2003; Verhelst & Wallner Reference Verhelst and Wallner2009). The strong differential diffusion of hydrogen leads to an amplification of small flame front perturbations such that strongly wrinkled flame fronts are observed with a significantly enhanced flame speed and strong variations of the local reaction rates (Matalon Reference Matalon2007). In a recent work, Berger et al. (Reference Berger, Kleinheinz, Attili and Pitsch2019) showed that thermodiffusive instabilities can lead to four times higher flame speeds compared with the unstretched laminar burning velocity in laminar lean hydrogen/air mixtures at ambient conditions. Also, in turbulent flames, effects of thermodiffusive instabilities were found to play a significant role (Chen & Im Reference Chen and Im2000; Im & Chen Reference Im and Chen2002; Hawkes & Chen Reference Hawkes and Chen2004; Chakraborty et al. Reference Chakraborty, Hawkes, Chen and Cant2008; Aspden, Day & Bell Reference Aspden, Day and Bell2011a,Reference Aspden, Day and Bellb,Reference Aspden, Day and Bellc, Reference Aspden, Day and Bell2015; Berger et al. Reference Berger, Attili and Pitsch2022b). It was shown by Aspden et al. (Reference Aspden, Day and Bell2011c), Lipatnikov et al. (Reference Lipatnikov, Lee, Dai, Wan and Sabelnikov2024) and Berger et al. (Reference Berger, Attili, Gauding and Pitsch2024) that thermodiffusive effects are present for a large range of Karlovitz numbers relevant for industrial applications. In particular, thermodiffusive instabilities that lead to the generation of flame surface area are sustained for a large range of relevant Karlovitz numbers (Berger et al. Reference Berger, Attili, Gauding and Pitsch2024). Most remarkably, thermodiffusive instabilities exhibit synergistic interactions with turbulent flows, leading to a further amplification of the turbulent flame speed (Berger et al. Reference Berger, Attili and Pitsch2022b). This results from high curvature and strain rate values in the turbulent environment, which further enhance the effects of differential diffusion. This leads to a strong enhancement of the local reactivity and local flame speed, which have been similarly observed experimentally (Wu et al. Reference Wu, Kwon, Driscoll and Faeth1991; Ahmed et al. Reference Ahmed, Thorne, Lawes, Hochgreb, Nivarti and Cant2021). The significantly different combustion behaviour of hydrogen has also been demonstrated by the experimental investigation of Cheng et al. (Reference Cheng, Littlejohn, Strakey and Sidwell2009), who operated a low swirl injector for gas turbine applications with hydrogen and methane. Increasing the hydrogen content in the fuel shifts the lifted flame close to the nozzle, eventually yielding a different shape of the flame. When operated with hydrogen, measurements of planar laser induced fluorescence of OH radicals show the occurrence of cellular patterns of the flame front, which are not visible in the methane flames (Day et al. Reference Day, Tachibana, Bell, Lijewski, Beckner and Cheng2015). These cellular patterns are clear markers of thermodiffusive instabilities (Berger et al. Reference Berger, Grinberg, Jürgens, Lapenna, Creta, Attili and Pitsch2023; Howarth, Hunt & Aspden Reference Howarth, Hunt and Aspden2023), indicating the presence and relevance of these instabilities in practical devices. Similarly, thermodiffusive instabilities have been shown to prevail under engine-relevant conditions (Chu et al. Reference Chu, Berger, Grenga, Wu and Pitsch2023), leading to a fourfold increase of the turbulent flame speed in turbulent spherical flames. An analysis of turbulent kinetic energy in the experiments of Cheng et al. (Reference Cheng, Littlejohn, Strakey and Sidwell2009) showed that hydrogen flames reveal a significant increase of turbulent kinetic energy within the flame front, also discussed e.g. by Chakraborty, Katragadda & Cant (Reference Chakraborty, Katragadda and Cant2011), indicating remarkable differences among the fuels. A numerical study using direct numerical simulations (DNS) (Day et al. Reference Day, Tachibana, Bell, Lijewski, Beckner and Cheng2015) highlighted the strong thermal diffusive effects in these flames.
As thermodiffusive instabilities and differential diffusion have a leading order effect on the flame dynamics of laminar and turbulent hydrogen flames, accurate models considering these effects are of utmost importance to enable predictive simulations of hydrogen flames. To capture the effects of such instabilities, a model needs to account for the differential diffusion of the fuel with respect to all other scalars, such as temperature, oxidizer and the combustion product. Bastiaans, Vreman & Pitsch (Reference Bastiaans, Vreman and Pitsch2007) proposed to solve transport equations for a hydrogen-based progress variable and temperature. A similar idea was pursued by Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) and Schlup & Blanquart (Reference Schlup and Blanquart2019). They suggested to solve transport equations for a water-based progress variable and a mixture fraction based on the species mass fractions, which represents a local equivalence ratio, and hence, explicitly represents the effects of differential diffusion. In both approaches, the local flame state is represented by unstretched premixed flamelets with varying equivalence ratio to model mixture fraction fluctuations within the flame front. Similarly, Böttler et al. (Reference Böttler, Lulic, Steinhausen, Wen, Hasse and Scholtissek2023) solved transport equations for the water, hydrogen and oxygen mass fractions to account for differential diffusion effects. While the models of Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) only solve two transport equations, the model of Böttler et al. (Reference Böttler, Lulic, Steinhausen, Wen, Hasse and Scholtissek2023) requires three transport equations as the differential diffusion effects are accounted for by two parameters, which are the local strain rate and curvature. The local flame state is represented by flamelets with varying strain rate and curvature using a composition space model (Scholtissek et al. Reference Scholtissek, Domingo, Vervisch and Hasse2019). One particular advantage of the formulation of Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) and Schlup & Blanquart (Reference Schlup and Blanquart2019) is that only the source term of progress variable requires modelling as the transport equation of mixture fraction is already closed. Further, Berger, Attili & Pitsch (Reference Berger, Attili and Pitsch2022a) showed in an a priori analysis of laminar DNS data that the local flame state is sufficiently well parametrized by mixture fraction and progress variable, while a parametrization based on progress variable, curvature and strain rate is less accurate. The latter set of parameters, which relates to the local flame morphology and flow field, describes the cause of differential diffusion effects in a flame, while mixture fraction represents the result of differential diffusion effects and, hence, yields a better parametrization of the instantaneous source terms. Thus, the modelling approach of Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) and Schlup & Blanquart (Reference Schlup and Blanquart2019), which has been developed for laminar flames, is chosen as a baseline in this work.
The models of Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) and Schlup & Blanquart (Reference Schlup and Blanquart2019) based on progress variable and mixture fraction are found to perform well for laminar flames. However, in turbulent flames, it is unclear whether a source term model can be built based on unstretched premixed flamelets similar to the laminar flames, as remarkably high values of curvature and strain rate are frequent in the turbulent environment, which significantly affect local flame dynamics (Berger et al. Reference Berger, Attili and Pitsch2022b). Whether these more extreme flame states can be well represented by unstretched premixed flamelets needs to be analysed. Similarly important, the effects of turbulence/flame subfilter interactions need to be modelled in large eddy simulations (LES), which is challenging as the flame front corrugations due to thermodiffusive instabilities are typically only partially resolved or are fully contained within the subfilter scales. In particular, the heat release and, hence, the consumption speed are strongly sensitive to the extremal values of the local flame front curvature, the information of which is difficult to retrieve from filtered fields that are less corrugated than the instantaneous flame front. Further modelling challenges arise due to the fact that joint subfilter distribution functions of two or more scalars need to be prescribed as at least two scalar transport equations, such as progress variable and mixture fraction, are needed to account for differential diffusion effects.
The objective of this work is to develop an LES combustion model for turbulent hydrogen flames that accounts for the effects of thermodiffusive instabilities. For this, the modelling framework of Schlup & Blanquart (Reference Schlup and Blanquart2019), which has been shown to account for these effects in laminar flames, is adopted and formulated for LES. In particular, a model for subfilter closure in LES is proposed to extend the modelling framework to turbulent flows. To pursue model development in a systematic way (Trisjono & Pitsch Reference Trisjono and Pitsch2015), the DNS data of Berger et al. (Reference Berger, Attili and Pitsch2022b) are employed. The DNS configuration represents a premixed hydrogen/air jet flame featuring realistic shear-driven turbulence, where the turbulent premixed flame is located in the shear layer of the jet. From the DNS data, model hypotheses for the subfilter closure in LES are formulated and tested in an a priori analysis. Thereafter, the performance of the newly proposed models is assessed in an a posteriori analysis by conducting LES of the DNS configuration. In § 2, the modelling framework to transport mixture fraction and progress variable is introduced. Then, the DNS data of Berger et al. (Reference Berger, Attili and Pitsch2022b) are briefly reviewed in § 3. In the a priori analysis in § 4, a combustion model is systematically developed by first identifying suitable model input parameters, then building a combustion model that includes a subfilter closure, and finally the a priori assessment of the model. In § 5, different combustion models are tested a posteriori by performing LES of the DNS configuration.
2. Modelling framework
In the formulation of Schlup & Blanquart (Reference Schlup and Blanquart2019), the water-based progress variable ![]() $C_{H_2O}$ and mixture fraction
$C_{H_2O}$ and mixture fraction ![]() $Z$ are defined as
$Z$ are defined as
where ![]() $Y_{{H_2O}}$ is the mass fraction of water and
$Y_{{H_2O}}$ is the mass fraction of water and ![]() $Y_{{H_2O,b}}$ is a constant, whose value is determined in the burned gas of the nominal mixture composition. For the mixture fraction, the stoichiometric coefficient
$Y_{{H_2O,b}}$ is a constant, whose value is determined in the burned gas of the nominal mixture composition. For the mixture fraction, the stoichiometric coefficient ![]() $\nu$ is defined by the ratio of the molar masses of oxygen and hydrogen as
$\nu$ is defined by the ratio of the molar masses of oxygen and hydrogen as ![]() $\nu =M_{O_2} / (2 M_{H_2})$. Here,
$\nu =M_{O_2} / (2 M_{H_2})$. Here, ![]() $Y_{O_2}$ is the mass fraction of molecular oxygen and
$Y_{O_2}$ is the mass fraction of molecular oxygen and ![]() $Y_{O_2,air}$ represents its value in air. Assuming a one-step global reaction for hydrogen combustion, Schlup & Blanquart (Reference Schlup and Blanquart2019) derived the set of equations
$Y_{O_2,air}$ represents its value in air. Assuming a one-step global reaction for hydrogen combustion, Schlup & Blanquart (Reference Schlup and Blanquart2019) derived the set of equations
Here, ![]() $\rho$ is the density,
$\rho$ is the density, ![]() $\boldsymbol {u}$ is the gas velocity,
$\boldsymbol {u}$ is the gas velocity, ![]() $D_{H_2O}$ and
$D_{H_2O}$ and ![]() $D^{T}_{H_2O}$ are the diffusion coefficients of water for molecular diffusion and for the Soret effect, respectively,
$D^{T}_{H_2O}$ are the diffusion coefficients of water for molecular diffusion and for the Soret effect, respectively, ![]() $T$ is the temperature, and
$T$ is the temperature, and ![]() $\dot {\omega }_{H_2O}$ is the source term of water due to chemical reactions. It is worth noting that the Soret effect cannot be neglected in hydrogen flames (Zhou et al. Reference Zhou, Hernandez-Perez, Shoshin, van Oijen and de Goey2017; Schlup & Blanquart Reference Schlup and Blanquart2018) and is considered in (2.3) and (2.4) by the term containing the gradient of temperature. Further, note that the diffusive flux in (2.3) typically also contains the additional effects of variations in molecular weight and a diffusion correction velocity, which are neglected as they were shown to be small by Schlup & Blanquart (Reference Schlup and Blanquart2019). Equation (2.3) is formulated for the mass fraction of
$\dot {\omega }_{H_2O}$ is the source term of water due to chemical reactions. It is worth noting that the Soret effect cannot be neglected in hydrogen flames (Zhou et al. Reference Zhou, Hernandez-Perez, Shoshin, van Oijen and de Goey2017; Schlup & Blanquart Reference Schlup and Blanquart2018) and is considered in (2.3) and (2.4) by the term containing the gradient of temperature. Further, note that the diffusive flux in (2.3) typically also contains the additional effects of variations in molecular weight and a diffusion correction velocity, which are neglected as they were shown to be small by Schlup & Blanquart (Reference Schlup and Blanquart2019). Equation (2.3) is formulated for the mass fraction of ![]() $Y_{H_2O}$, but can be written in terms of
$Y_{H_2O}$, but can be written in terms of ![]() $C_{H_2O}$ by dividing by the constant value
$C_{H_2O}$ by dividing by the constant value ![]() $Y_{{H_2O,b}}$. The diffusion coefficient of mixture fraction
$Y_{{H_2O,b}}$. The diffusion coefficient of mixture fraction ![]() $D_{Z_{C_{H_2O}}}$ is linked to the diffusion coefficients of hydrogen and oxygen as
$D_{Z_{C_{H_2O}}}$ is linked to the diffusion coefficients of hydrogen and oxygen as
where the weighting factors ![]() $Y_{H_2,F}$ and
$Y_{H_2,F}$ and ![]() $Y_{O_2,air}$ are the mass fractions of hydrogen and oxygen in the fuel stream and air, respectively. The index ‘
$Y_{O_2,air}$ are the mass fractions of hydrogen and oxygen in the fuel stream and air, respectively. The index ‘![]() ${Z_{C_{H_2O}}}$’ indicates that this is the diffusion coefficient of mixture fraction when using a water-based progress variable. The last two terms on the right-hand side of (2.4) represent source terms that are linked to the difference of the diffusion coefficients of hydrogen and oxygen concerning molecular diffusion and the Soret effect, which leads to mixture fraction variations in a premixed flame. Here,
${Z_{C_{H_2O}}}$’ indicates that this is the diffusion coefficient of mixture fraction when using a water-based progress variable. The last two terms on the right-hand side of (2.4) represent source terms that are linked to the difference of the diffusion coefficients of hydrogen and oxygen concerning molecular diffusion and the Soret effect, which leads to mixture fraction variations in a premixed flame. Here, ![]() $D_{Z_{C_{H_2O}}}^*$ and
$D_{Z_{C_{H_2O}}}^*$ and ![]() $D_{Z}^T$ are given as
$D_{Z}^T$ are given as
 $$\begin{gather}D_{Z}^T = \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) . \end{gather}$$
$$\begin{gather}D_{Z}^T = \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) . \end{gather}$$In this work, two model formulations will be investigated, using a water-based and a hydrogen-based progress variable; therefore, a similar set of equations can be derived for a hydrogen-based progress variable. The latter is defined as
where ![]() $Y_{{H_2,u}}$ is the value of the hydrogen mass fraction in the unburned gas. As the two definitions feature different characteristics, the effects of the two definitions on the LES predictions are assessed in this work. In particular, a water-based progress variable
$Y_{{H_2,u}}$ is the value of the hydrogen mass fraction in the unburned gas. As the two definitions feature different characteristics, the effects of the two definitions on the LES predictions are assessed in this work. In particular, a water-based progress variable ![]() $C_{H_2O}$ possesses sub- and super-unity values in the post-flame region similar to the temperature, while the hydrogen-based progress variable
$C_{H_2O}$ possesses sub- and super-unity values in the post-flame region similar to the temperature, while the hydrogen-based progress variable ![]() $C_{H_2}$ is strictly bound to
$C_{H_2}$ is strictly bound to ![]() $C_{H_2} \in [0,1]$ and the value
$C_{H_2} \in [0,1]$ and the value ![]() $C_{H_2} = 1$ unambiguously defines the equilibrium state of the burned gas. This property of
$C_{H_2} = 1$ unambiguously defines the equilibrium state of the burned gas. This property of ![]() $C_{H_2}$ is important for the formulation of a model for the subfilter probability density function (p.d.f.) as discussed further below.
$C_{H_2}$ is important for the formulation of a model for the subfilter probability density function (p.d.f.) as discussed further below.
Analogously to (2.3) and (2.4), the following set of equations is derived assuming a one-step global reaction:
Note that the diffusion coefficients ![]() ${D}_{Z}$ and
${D}_{Z}$ and ![]() ${D}^*_{Z}$ differ from those defined in (2.4). They are given as
${D}^*_{Z}$ differ from those defined in (2.4). They are given as
while the definition of ![]() $D_{Z}^T$ remains unchanged. A detailed derivation of (2.10) is given in Appendix A.
$D_{Z}^T$ remains unchanged. A detailed derivation of (2.10) is given in Appendix A.
To close the system of equations in (2.3) and (2.4) for a water-based progress variable formulation, the source term ![]() $\dot {\omega }_{H_2O}$ needs to be modelled as a function of the two transported scalars,
$\dot {\omega }_{H_2O}$ needs to be modelled as a function of the two transported scalars, ![]() $Y_{H_2O}$ and
$Y_{H_2O}$ and ![]() $Z$. Analogously, to close the set of equations for a hydrogen-based progress variable, cf. (2.9) and (2.10), the source term of hydrogen
$Z$. Analogously, to close the set of equations for a hydrogen-based progress variable, cf. (2.9) and (2.10), the source term of hydrogen ![]() $\dot {\omega }_{H_2}$ needs to be expressed in terms of
$\dot {\omega }_{H_2}$ needs to be expressed in terms of ![]() $Y_{H_2}$ and
$Y_{H_2}$ and ![]() $Z$. Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) proposed to represent the local flame state, which is parametrized by the two transported scalars, by a set of unstretched premixed flamelets with different equivalence ratios. Essentially, the variation of the nominal equivalence ratio of the flamelets mimics the local variations of the equivalence ratio due to differential diffusion effects within the flame front. Thereby, a large fraction of states of mixture fraction and progress variable within laminar hydrogen flames can be covered and good a priori and a posteriori predictions are achieved. In particular, Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) assessed the model for planar laminar hydrogen flames that develop corrugations due to the instabilities and for one-dimensional spherical flames.
$Z$. Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) proposed to represent the local flame state, which is parametrized by the two transported scalars, by a set of unstretched premixed flamelets with different equivalence ratios. Essentially, the variation of the nominal equivalence ratio of the flamelets mimics the local variations of the equivalence ratio due to differential diffusion effects within the flame front. Thereby, a large fraction of states of mixture fraction and progress variable within laminar hydrogen flames can be covered and good a priori and a posteriori predictions are achieved. In particular, Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013) assessed the model for planar laminar hydrogen flames that develop corrugations due to the instabilities and for one-dimensional spherical flames.
In this work, the modelling framework of Schlup & Blanquart (Reference Schlup and Blanquart2019) is extended to turbulent hydrogen flames. For an LES formulation, (2.3), (2.4), (2.9) and (2.10) are filtered, yielding the transport equations
 $$\begin{gather} \frac{ \partial (\bar{\rho} \tilde{Y}_{i})}{\partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Y}_{i}) = \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Y}_{i} - \bar{\rho} \widetilde{\boldsymbol{u} Y_{i}}) + \boldsymbol{\nabla} \boldsymbol{\cdot} \left(\bar{\rho} \widetilde{D_{i}} \boldsymbol{\nabla} \tilde{Y}_{i} + \bar{\rho} \widetilde{\left(\frac{D^{T}_{i}}{ \rho T}\right)}\boldsymbol{\nabla} \tilde{T} \right) + \bar{\dot{\omega}}_{i} , \end{gather}$$
$$\begin{gather} \frac{ \partial (\bar{\rho} \tilde{Y}_{i})}{\partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Y}_{i}) = \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Y}_{i} - \bar{\rho} \widetilde{\boldsymbol{u} Y_{i}}) + \boldsymbol{\nabla} \boldsymbol{\cdot} \left(\bar{\rho} \widetilde{D_{i}} \boldsymbol{\nabla} \tilde{Y}_{i} + \bar{\rho} \widetilde{\left(\frac{D^{T}_{i}}{ \rho T}\right)}\boldsymbol{\nabla} \tilde{T} \right) + \bar{\dot{\omega}}_{i} , \end{gather}$$ $$\begin{gather}\begin{aligned}\frac{ \partial (\bar{\rho} \tilde{Z})}{\partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Z}) &= \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Z} - \bar{\rho} \widetilde{\boldsymbol{u} Z}) + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{D}_{Z_{C_{i}}} \boldsymbol{\nabla} \tilde{Z})\\ &\quad {{+}/{-}} \ \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{D}^*_{Z_{C_{i}}} \boldsymbol{\nabla} \tilde{Y}_{i}) + \bar{\rho} \widetilde{\left(\frac{D^{T}_{Z}}{ \rho T}\right)} \boldsymbol{\nabla} \tilde{T} \quad \text{with `}{+}/{-}\text{' for }{\rm H}_2/{\rm H}_2{\rm O}, \end{aligned}\end{gather}$$
$$\begin{gather}\begin{aligned}\frac{ \partial (\bar{\rho} \tilde{Z})}{\partial t} + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Z}) &= \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{\boldsymbol{u}} \tilde{Z} - \bar{\rho} \widetilde{\boldsymbol{u} Z}) + \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{D}_{Z_{C_{i}}} \boldsymbol{\nabla} \tilde{Z})\\ &\quad {{+}/{-}} \ \boldsymbol{\nabla} \boldsymbol{\cdot} (\bar{\rho} \tilde{D}^*_{Z_{C_{i}}} \boldsymbol{\nabla} \tilde{Y}_{i}) + \bar{\rho} \widetilde{\left(\frac{D^{T}_{Z}}{ \rho T}\right)} \boldsymbol{\nabla} \tilde{T} \quad \text{with `}{+}/{-}\text{' for }{\rm H}_2/{\rm H}_2{\rm O}, \end{aligned}\end{gather}$$
where the ![]() $\overline {(\cdots )}$ operator denotes filtering and the
$\overline {(\cdots )}$ operator denotes filtering and the ![]() $\widetilde {(\cdots )}$ operator represents a density-weighted filtering, referred to as Favre filtering. Note that in (2.13), the index
$\widetilde {(\cdots )}$ operator represents a density-weighted filtering, referred to as Favre filtering. Note that in (2.13), the index ![]() $i$ is introduced to distinguish between the two different progress variable definitions. It is worth noting that (2.13) and (2.14) are obtained by neglecting the subfilter correlation between the diffusion coefficients and the scalar gradients; a common assumption in LES modelling, which, however, introduces a certain modelling error (Fiorina et al. Reference Fiorina, Vicquelin, Auzillon, Darabiha, Gicquel and Veynante2010; Nambully et al. Reference Nambully, Domingo, Moureau and Vervisch2014; Domingo & Vervisch Reference Domingo and Vervisch2015) that will be discussed in the following. The filtered transport equations given by (2.13) and (2.14) feature several unclosed terms. Following Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), the subfilter scalar flux can be closed by a dynamic Smagorinsky model (Pierce & Moin Reference Pierce and Moin1998). Further, the filtered chemical source term in (2.13) and the filtered transport coefficients, e.g. the molecular and thermal diffusion coefficients and the viscosity in the momentum equation, require closure, for which a model is proposed and assessed in this work.
$i$ is introduced to distinguish between the two different progress variable definitions. It is worth noting that (2.13) and (2.14) are obtained by neglecting the subfilter correlation between the diffusion coefficients and the scalar gradients; a common assumption in LES modelling, which, however, introduces a certain modelling error (Fiorina et al. Reference Fiorina, Vicquelin, Auzillon, Darabiha, Gicquel and Veynante2010; Nambully et al. Reference Nambully, Domingo, Moureau and Vervisch2014; Domingo & Vervisch Reference Domingo and Vervisch2015) that will be discussed in the following. The filtered transport equations given by (2.13) and (2.14) feature several unclosed terms. Following Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), the subfilter scalar flux can be closed by a dynamic Smagorinsky model (Pierce & Moin Reference Pierce and Moin1998). Further, the filtered chemical source term in (2.13) and the filtered transport coefficients, e.g. the molecular and thermal diffusion coefficients and the viscosity in the momentum equation, require closure, for which a model is proposed and assessed in this work.
3. DNS database description
For the a priori analysis, the large-scale DNS of a lean premixed hydrogen/air flame in a slot burner configuration of Berger et al. (Reference Berger, Attili and Pitsch2022b) is employed. The DNS was performed at a jet Reynolds number of ![]() $Re_{Jet}=11\,000$ and Karlovitz number of
$Re_{Jet}=11\,000$ and Karlovitz number of ![]() $Ka \approx 20$. The latter is evaluated from the Kolmogorov length of the local flow field and the laminar flame thickness
$Ka \approx 20$. The latter is evaluated from the Kolmogorov length of the local flow field and the laminar flame thickness ![]() $l_{F}$, where
$l_{F}$, where ![]() $l_{F}$ is based on the maximum temperature gradient of an unstretched flamelet. The corresponding turbulent Reynolds number
$l_{F}$ is based on the maximum temperature gradient of an unstretched flamelet. The corresponding turbulent Reynolds number ![]() $Re_{t}$ averaged in the inflow channel yields
$Re_{t}$ averaged in the inflow channel yields ![]() $Re_{t}=110$. (The turbulent Reynolds number is defined as
$Re_{t}=110$. (The turbulent Reynolds number is defined as ![]() $Re_{t} = {u' l_{t} }/{ \bar {\nu }}$, where the turbulence intensity
$Re_{t} = {u' l_{t} }/{ \bar {\nu }}$, where the turbulence intensity ![]() $u'$ and integral scale
$u'$ and integral scale ![]() $l_{t}$ are determined as
$l_{t}$ are determined as ![]() ${u'}= \sqrt {\tfrac {2}{3} \tilde {k}}$ and
${u'}= \sqrt {\tfrac {2}{3} \tilde {k}}$ and ![]() $l_{t} = {{u'}^3}/{\tilde {\epsilon }}$. The Favre-averaged turbulent kinetic energy
$l_{t} = {{u'}^3}/{\tilde {\epsilon }}$. The Favre-averaged turbulent kinetic energy ![]() $\tilde {k}$ and Favre-averaged energy dissipation rate
$\tilde {k}$ and Favre-averaged energy dissipation rate ![]() $\tilde {\epsilon }$ are computed according to Pantano, Sarkar & Williams (Reference Pantano, Sarkar and Williams2003) and can be found from Berger et al. (Reference Berger, Attili and Pitsch2022b).) In the DNS, detailed chemistry is used and the Soret effect is considered, which is important for hydrogen flames (Zhou et al. Reference Zhou, Hernandez-Perez, Shoshin, van Oijen and de Goey2017; Schlup & Blanquart Reference Schlup and Blanquart2018); characteristic simulation parameters are listed in table 1. A snapshot of the temperature field is shown in figure 1(a). Unburned mixture is injected within the slot and burned gas is used as a coflow. The unburned mixture features an equivalence ratio of
$\tilde {\epsilon }$ are computed according to Pantano, Sarkar & Williams (Reference Pantano, Sarkar and Williams2003) and can be found from Berger et al. (Reference Berger, Attili and Pitsch2022b).) In the DNS, detailed chemistry is used and the Soret effect is considered, which is important for hydrogen flames (Zhou et al. Reference Zhou, Hernandez-Perez, Shoshin, van Oijen and de Goey2017; Schlup & Blanquart Reference Schlup and Blanquart2018); characteristic simulation parameters are listed in table 1. A snapshot of the temperature field is shown in figure 1(a). Unburned mixture is injected within the slot and burned gas is used as a coflow. The unburned mixture features an equivalence ratio of ![]() $\phi =0.4$, a temperature of
$\phi =0.4$, a temperature of ![]() $T_{u}=298\,{\rm K}$ and the pressure is
$T_{u}=298\,{\rm K}$ and the pressure is ![]() $1$ bar. The nominal laminar unstretched burning velocity
$1$ bar. The nominal laminar unstretched burning velocity ![]() $s_{L}$ is
$s_{L}$ is ![]() $17\,{\rm cm}\,{\rm s}^{-1}$ and the laminar flame thickness
$17\,{\rm cm}\,{\rm s}^{-1}$ and the laminar flame thickness ![]() $l_{F}$ is 0.714 mm. The coflow gas is at the adiabatic flame temperature and from figure 1(a), it is evident that super-adiabatic temperatures are present in the hydrogen/air flame. This is a clear marker of thermodiffusive instabilities and has been discussed in detail by Giannakopoulos et al. (Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). In particular, the differential diffusion of hydrogen within the flame front leads to locally leaner and richer mixtures. As discussed by Berger et al. (Reference Berger, Attili and Pitsch2022b), locally richer mixtures are preferentially formed due to the positive mean strain rate induced by the small-scale turbulent fluctuations (Luca et al. Reference Luca, Attili, Schiavo, Creta and Bisetti2019; Berger et al. Reference Berger, Attili and Pitsch2022b, Reference Berger, Attili, Gauding and Pitsch2024). In figure 1(b), the fluctuations of the local equivalence ratio are shown by means of mixture fraction.
$l_{F}$ is 0.714 mm. The coflow gas is at the adiabatic flame temperature and from figure 1(a), it is evident that super-adiabatic temperatures are present in the hydrogen/air flame. This is a clear marker of thermodiffusive instabilities and has been discussed in detail by Giannakopoulos et al. (Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). In particular, the differential diffusion of hydrogen within the flame front leads to locally leaner and richer mixtures. As discussed by Berger et al. (Reference Berger, Attili and Pitsch2022b), locally richer mixtures are preferentially formed due to the positive mean strain rate induced by the small-scale turbulent fluctuations (Luca et al. Reference Luca, Attili, Schiavo, Creta and Bisetti2019; Berger et al. Reference Berger, Attili and Pitsch2022b, Reference Berger, Attili, Gauding and Pitsch2024). In figure 1(b), the fluctuations of the local equivalence ratio are shown by means of mixture fraction.
Table 1. Simulation parameters of the turbulent premixed hydrogen flame. Left column, slot width ![]() $H$ and bulk velocity
$H$ and bulk velocity ![]() $U$ of central jet; velocity
$U$ of central jet; velocity ![]() $U_{Coflow}$ of laminar coflow; grid resolution
$U_{Coflow}$ of laminar coflow; grid resolution ![]() $\delta _{DNS}$; jet Reynolds number
$\delta _{DNS}$; jet Reynolds number ![]() $Re_{Jet}$; the turbulent Reynolds number
$Re_{Jet}$; the turbulent Reynolds number ![]() $Re_{t}$ in the inflow channel; characteristic Karlovitz number
$Re_{t}$ in the inflow channel; characteristic Karlovitz number ![]() $Ka$ and Kolmogorov length scale
$Ka$ and Kolmogorov length scale ![]() $\eta$ on the flame sheet; domain size
$\eta$ on the flame sheet; domain size ![]() $L_{i}$; and number of grid points
$L_{i}$; and number of grid points ![]() $N_{i}$ in each direction. Right column, unburned temperature
$N_{i}$ in each direction. Right column, unburned temperature ![]() $T_{u}$; pressure
$T_{u}$; pressure ![]() $p$; equivalence ratio
$p$; equivalence ratio ![]() $\phi$; and laminar burning velocity
$\phi$; and laminar burning velocity ![]() $s_{L}$ and thermal flame thickness
$s_{L}$ and thermal flame thickness ![]() $l_{F}$ of an unstretched laminar flame.
$l_{F}$ of an unstretched laminar flame.


Figure 1. (a) Instantaneous temperature field of the DNS of a hydrogen/air flame in a slot burner configuration. (b) Close-up of the mixture fraction field for the red dashed box in panel (a).
Note that Berger et al. (Reference Berger, Attili and Pitsch2022b) also performed an additional DNS of the same configuration, in which the effects of differential diffusion were artificially suppressed. This was achieved by setting the Lewis number of all species to unity and neglecting the Soret effect. While it is not the focus of this work to perform and assess LES of this DNS case, an LES of this case is discussed at the end of the paper to allow for a complete assessment of the presented modelling framework for flames with and without differential diffusion effects.
Unless noted differently, the DNS that includes differential diffusion effects will be discussed and is referred to as DNS.
4. A priori analysis
4.1. Optimal parameters for source term model
For the systematic development of any model and, in particular, a model for the progress variable source term ![]() $\dot {\omega }_{i}$, it is important to first identify the relevant input parameters, with which the quantity of interest can be best parametrized. This is achieved in an optimal estimator analysis (Moreau, Teytaud & Bertoglio Reference Moreau, Teytaud and Bertoglio2006; Berger et al. Reference Berger, Kleinheinz, Mueller and Pitsch2018), in which the capability of a set of parameters
$\dot {\omega }_{i}$, it is important to first identify the relevant input parameters, with which the quantity of interest can be best parametrized. This is achieved in an optimal estimator analysis (Moreau, Teytaud & Bertoglio Reference Moreau, Teytaud and Bertoglio2006; Berger et al. Reference Berger, Kleinheinz, Mueller and Pitsch2018), in which the capability of a set of parameters ![]() $\boldsymbol {\psi }$, e.g.
$\boldsymbol {\psi }$, e.g. ![]() $\boldsymbol {\psi } = [C_{H_2O},Z]$, to parametrize a target quantity
$\boldsymbol {\psi } = [C_{H_2O},Z]$, to parametrize a target quantity ![]() $Q$, e.g.
$Q$, e.g. ![]() $Q=\dot {\omega }_{C_{H_2O}}$, is quantified by an error norm referred to as irreducible error. The amount of scatter of
$Q=\dot {\omega }_{C_{H_2O}}$, is quantified by an error norm referred to as irreducible error. The amount of scatter of ![]() $Q$ with respect to the conditional mean
$Q$ with respect to the conditional mean ![]() $\langle Q \mid \boldsymbol {\psi } \rangle$ is measured by the quadratic error norm and the parametrization is good if small irreducible errors are observed. Further details on the concept of the optimal estimator and technical details are provided by Moreau et al. (Reference Moreau, Teytaud and Bertoglio2006) and Berger et al. (Reference Berger, Kleinheinz, Mueller and Pitsch2018). In the following, the irreducible errors are conditionally averaged with respect to progress variable
$\langle Q \mid \boldsymbol {\psi } \rangle$ is measured by the quadratic error norm and the parametrization is good if small irreducible errors are observed. Further details on the concept of the optimal estimator and technical details are provided by Moreau et al. (Reference Moreau, Teytaud and Bertoglio2006) and Berger et al. (Reference Berger, Kleinheinz, Mueller and Pitsch2018). In the following, the irreducible errors are conditionally averaged with respect to progress variable ![]() $C_{i}$, defined as
$C_{i}$, defined as
where ![]() $\dot {\omega }_{i}$ represents the source term for either
$\dot {\omega }_{i}$ represents the source term for either ![]() $Y_{H_2O}$ or
$Y_{H_2O}$ or ![]() $Y_{H_2}$. The irreducible error
$Y_{H_2}$. The irreducible error ![]() $\epsilon _{{irr}^*}^2$ is normalized by the maximum value of the conditionally averaged source term
$\epsilon _{{irr}^*}^2$ is normalized by the maximum value of the conditionally averaged source term ![]() $\langle \dot {\omega }_{i} \mid C_{i} \rangle$, yielding
$\langle \dot {\omega }_{i} \mid C_{i} \rangle$, yielding
With this normalization, a value of unity indicates irreducible errors that are as large as the maximum value of the average source term within the flame front. In the following, only the analysis based on the hydrogen-based progress variable ![]() $C_{i}=C_{H_2}$ is presented since the analysis concerning the water-based progress variable yields similar findings.
$C_{i}=C_{H_2}$ is presented since the analysis concerning the water-based progress variable yields similar findings.
Figure 2 shows the irreducible errors for different parametrizations of the progress variable source term with different sets of parameters evaluated by means of the DNS data. As the development of an LES combustion model is pursued, three different filter sizes are shown: the unfiltered fields, and two filter sizes ![]() $\varDelta$ that correspond to one and two flame thicknesses
$\varDelta$ that correspond to one and two flame thicknesses ![]() $l_{F}$. For the filtering procedure, a box-filter is used.
$l_{F}$. For the filtering procedure, a box-filter is used.

Figure 2. Irreducible errors of progress variable source term using different sets of parameters. Analysis for (a) unfiltered fields and (b,c) filtered fields with two different filter sizes ![]() $\varDelta$. Note that
$\varDelta$. Note that ![]() $\varDelta = l_{F}$ and
$\varDelta = l_{F}$ and ![]() $\varDelta = 2 l_{F}$ correspond to filtering of 10 and 20 grid points in the DNS, respectively.
$\varDelta = 2 l_{F}$ correspond to filtering of 10 and 20 grid points in the DNS, respectively.
For the unfiltered fields, irreducible errors are shown if parametrizing the progress variable source term only by progress variable, e.g. ![]() $\boldsymbol {\psi } = [C_{H_2}]$, or by progress variable and mixture fraction, e.g.
$\boldsymbol {\psi } = [C_{H_2}]$, or by progress variable and mixture fraction, e.g. ![]() $\boldsymbol {\psi } = [C_{H_2},Z]$. Using only progress variable for parametrization, the average fluctuations of the source term are as large as 70 % of the mean value at a progress variable of
$\boldsymbol {\psi } = [C_{H_2},Z]$. Using only progress variable for parametrization, the average fluctuations of the source term are as large as 70 % of the mean value at a progress variable of ![]() $C_{H_2}=0.7$, indicating strong variations, which cannot be described solely by progress variable. Consistent with the analyses of Berger et al. (Reference Berger, Attili and Pitsch2022a), including mixture fraction significantly improves the parametrization of the source term as it intrinsically captures the effects of differential diffusion. For instance, the maximum of the conditionally averaged irreducible errors in figure 2 drops from
$C_{H_2}=0.7$, indicating strong variations, which cannot be described solely by progress variable. Consistent with the analyses of Berger et al. (Reference Berger, Attili and Pitsch2022a), including mixture fraction significantly improves the parametrization of the source term as it intrinsically captures the effects of differential diffusion. For instance, the maximum of the conditionally averaged irreducible errors in figure 2 drops from ![]() $\max (\epsilon _{irr}^2) = 0.66$ for the parametrization only by progress variable to a value of
$\max (\epsilon _{irr}^2) = 0.66$ for the parametrization only by progress variable to a value of ![]() $\max (\epsilon _{irr}^2) = 0.012$ if additionally including mixture fraction. Thus, the instantaneous progress variable source term
$\max (\epsilon _{irr}^2) = 0.012$ if additionally including mixture fraction. Thus, the instantaneous progress variable source term ![]() $\dot {\omega }_{H_2}$ may be parametrized as
$\dot {\omega }_{H_2}$ may be parametrized as ![]() $\dot {\omega }_{H_2}(C_{H_2},Z)$. This also indicates that the assumption of a one-step global reaction that is used to defined the mixture fraction in (2.2) does not negatively impact the parametrization of the detailed chemical reactions by progress variable and mixture fraction. The parametrization of the source term by the different parameter sets is visualized in figure 3, where two scatters of the DNS data are shown. If the source term is parametrized by progress variable only, significant scattering can be seen, while in figure 3(b), where the source term is parametrized by progress variable and mixture fraction, a good parametrization is achieved as the data collapse onto a manifold.
$\dot {\omega }_{H_2}(C_{H_2},Z)$. This also indicates that the assumption of a one-step global reaction that is used to defined the mixture fraction in (2.2) does not negatively impact the parametrization of the detailed chemical reactions by progress variable and mixture fraction. The parametrization of the source term by the different parameter sets is visualized in figure 3, where two scatters of the DNS data are shown. If the source term is parametrized by progress variable only, significant scattering can be seen, while in figure 3(b), where the source term is parametrized by progress variable and mixture fraction, a good parametrization is achieved as the data collapse onto a manifold.

Figure 3. Parametrization of source term ![]() $\dot {\omega }_{H_2}$ if using (a) progress variable and (b) progress variable and mixture fraction to condition the DNS data. Additionally, the conditional mean
$\dot {\omega }_{H_2}$ if using (a) progress variable and (b) progress variable and mixture fraction to condition the DNS data. Additionally, the conditional mean ![]() $\langle \dot {\omega }_{H_2} \mid C_{H_2} \rangle$ is shown in panel (a).
$\langle \dot {\omega }_{H_2} \mid C_{H_2} \rangle$ is shown in panel (a).
For the filtered fields, additional input parameters need to be considered to parametrize the filtered progress variable source term ![]() $\bar {\dot {\omega }}_{H_2}$. While the instantaneous progress variable source term
$\bar {\dot {\omega }}_{H_2}$. While the instantaneous progress variable source term ![]() $\dot {\omega }_{H_2}$ only depends on progress variable and mixture fraction, the filtered progress variable source term
$\dot {\omega }_{H_2}$ only depends on progress variable and mixture fraction, the filtered progress variable source term ![]() $\bar {\dot {\omega }}_{H_2}$ is also affected by the subfilter distribution, which can be represented by the higher-order moments of progress variable and mixture fraction, such as
$\bar {\dot {\omega }}_{H_2}$ is also affected by the subfilter distribution, which can be represented by the higher-order moments of progress variable and mixture fraction, such as ![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\tilde {Z}$,
$\tilde {Z}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ etc. This can be formally written as
$\widetilde {{C_{H_2}^{{''}^2}}}$ etc. This can be formally written as
Note that ![]() $\widetilde {{Q^{{''}^2}}}$ denotes the subfilter variance of a quantity
$\widetilde {{Q^{{''}^2}}}$ denotes the subfilter variance of a quantity ![]() $Q$. Thus, for the filtered fields, irreducible errors of several more different parameter sets are investigated in figure 2(b,c) as combinations of different subfilter moments are assessed.
$Q$. Thus, for the filtered fields, irreducible errors of several more different parameter sets are investigated in figure 2(b,c) as combinations of different subfilter moments are assessed.
While progress variable and mixture fraction describe the unfiltered source term very well, it is evident that their parametrization capability is significantly reduced for increasing filter sizes. In particular, the irreducible error with ![]() $\boldsymbol {\psi } = [\widetilde {C_{H_2}},\tilde {Z}]$ is close to
$\boldsymbol {\psi } = [\widetilde {C_{H_2}},\tilde {Z}]$ is close to ![]() $\boldsymbol {\psi } = [\widetilde {C_{H_2}}]$ in figure 2(c). Also, using only progress variable and any of the second order moments does not reduce irreducible errors significantly. Thus, three parameters are needed and the best parametrization is achieved with the set
$\boldsymbol {\psi } = [\widetilde {C_{H_2}}]$ in figure 2(c). Also, using only progress variable and any of the second order moments does not reduce irreducible errors significantly. Thus, three parameters are needed and the best parametrization is achieved with the set ![]() $\boldsymbol {\psi } = [\widetilde {C_{H_2}},\tilde {Z},\widetilde {{C_{H_2}^{{''}^2}}}]$. However, adding a fourth parameter, e.g. a second variance, does not yield any significant further reduction and, hence, is not needed. This is also quantitatively assessed by the maximum irreducible errors of each parametrization, which are provided in Appendix B. It is worth noting that using the variance of progress variable
$\boldsymbol {\psi } = [\widetilde {C_{H_2}},\tilde {Z},\widetilde {{C_{H_2}^{{''}^2}}}]$. However, adding a fourth parameter, e.g. a second variance, does not yield any significant further reduction and, hence, is not needed. This is also quantitatively assessed by the maximum irreducible errors of each parametrization, which are provided in Appendix B. It is worth noting that using the variance of progress variable ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ in addition to
$\widetilde {{C_{H_2}^{{''}^2}}}$ in addition to ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\tilde {Z}$ yields lower irreducible errors than using the variance of mixture fraction
$\tilde {Z}$ yields lower irreducible errors than using the variance of mixture fraction ![]() $\widetilde {{Z^{{''}^2}}}$, indicating a higher dependence of the subfilter source term fluctuations on the subfilter fluctuations of progress variable than of mixture fraction. Thus, an LES combustion model for thermodiffusively unstable flames should be based on progress variable, mixture fraction and the variance of progress variable. Similar conclusions are drawn from an optimal estimator analysis for the water-based progress variable, showing that
$\widetilde {{Z^{{''}^2}}}$, indicating a higher dependence of the subfilter source term fluctuations on the subfilter fluctuations of progress variable than of mixture fraction. Thus, an LES combustion model for thermodiffusively unstable flames should be based on progress variable, mixture fraction and the variance of progress variable. Similar conclusions are drawn from an optimal estimator analysis for the water-based progress variable, showing that ![]() $\bar {\dot {\omega }}_{H_2O}$ is well parametrized by the parameter set
$\bar {\dot {\omega }}_{H_2O}$ is well parametrized by the parameter set ![]() $\boldsymbol {\psi } = [\widetilde {C_{H_2O}},\tilde {Z},\widetilde {{C_{H_2O}^{{''}^2}}}]$.
$\boldsymbol {\psi } = [\widetilde {C_{H_2O}},\tilde {Z},\widetilde {{C_{H_2O}^{{''}^2}}}]$.
4.2. Formulation of source term model
Based on the findings of the optimal estimator analysis, a model for the progress variable source term is formulated in this section. A presumed p.d.f. approach is chosen and the filtered progress variable source term ![]() $\bar {\dot {\omega }}_{H_2}$ is expressed as
$\bar {\dot {\omega }}_{H_2}$ is expressed as
Here, ![]() $\tilde {\mathcal {P}}(C_{H_2},Z)$ is the density-weighted joint subfilter p.d.f. of progress variable and mixture fraction, and hence, to obtain the filtered source term
$\tilde {\mathcal {P}}(C_{H_2},Z)$ is the density-weighted joint subfilter p.d.f. of progress variable and mixture fraction, and hence, to obtain the filtered source term ![]() $\bar {\dot {\omega }}_{H_2}$, the inverse density-weighting in (4.4) is performed. Favre-filtered quantities, such as the progress variable, are obtained as
$\bar {\dot {\omega }}_{H_2}$, the inverse density-weighting in (4.4) is performed. Favre-filtered quantities, such as the progress variable, are obtained as
while the filtered density is given by
Similar to the previous section, the discussion is based on the modelling of ![]() $\bar {\dot {\omega }}_{H_2}$, while the model for the source term
$\bar {\dot {\omega }}_{H_2}$, while the model for the source term ![]() $\bar {\dot {\omega }}_{H_2O}$ of the water-based progress variable is discussed at the end of the section.
$\bar {\dot {\omega }}_{H_2O}$ of the water-based progress variable is discussed at the end of the section.
The following discussion of the model formulation is structured in three parts: first, a flamelet-based model to represent the unfiltered source term ![]() $\dot {\omega }_{H_2}(C_{H_2},Z)$ is discussed; second, a presumed p.d.f. model of
$\dot {\omega }_{H_2}(C_{H_2},Z)$ is discussed; second, a presumed p.d.f. model of ![]() $\tilde {\mathcal {P}}(C_{H_2},Z)$ is introduced and assessed by the DNS data; third, the model formulation based on a water-based progress variable is presented.
$\tilde {\mathcal {P}}(C_{H_2},Z)$ is introduced and assessed by the DNS data; third, the model formulation based on a water-based progress variable is presented.
4.2.1. Modelling the unfiltered source term
First, a model for ![]() $\dot {\omega }_{H_2}(C_{H_2},Z)$ is required. For this, figure 4 shows the joint p.d.f. of progress variable and mixture fraction in the DNS, which displays the range of possible states in the turbulent flame, and compares different sets of representative flamelets with the turbulent flame states. In figure 4(a), strained flamelets with different strain rates
$\dot {\omega }_{H_2}(C_{H_2},Z)$ is required. For this, figure 4 shows the joint p.d.f. of progress variable and mixture fraction in the DNS, which displays the range of possible states in the turbulent flame, and compares different sets of representative flamelets with the turbulent flame states. In figure 4(a), strained flamelets with different strain rates ![]() $a$ and an equivalence ratio of
$a$ and an equivalence ratio of ![]() $\phi =0.4$ are shown. These flamelets are generated in FlameMaster (Pitsch Reference Pitsch1998) by computing a counterflow flame, in which burned and unburned mixtures are injected towards each other. Both streams feature an equivalence ratio of
$\phi =0.4$ are shown. These flamelets are generated in FlameMaster (Pitsch Reference Pitsch1998) by computing a counterflow flame, in which burned and unburned mixtures are injected towards each other. Both streams feature an equivalence ratio of ![]() $\phi =0.4$ and a pressure of
$\phi =0.4$ and a pressure of ![]() $p=1$ bar, while the temperatures are set to
$p=1$ bar, while the temperatures are set to ![]() $T_{u}=298\,{\rm K}$ in the unburned gas and to
$T_{u}=298\,{\rm K}$ in the unburned gas and to ![]() $T_{b}=1418\,{\rm K}$ in the burned gas, where the latter represents the adiabatic flame temperature. The outermost flamelets represent the unstretched flamelet (dotted black curve) and the conditions when extinction occurs (yellow curve), e.g. defined by a rapid reduction of reaction rates if strain rate is further increased. In figure 4(b), the joint p.d.f. is compared with a set of unstretched premixed flamelets with different equivalence ratios, ranging from
$T_{b}=1418\,{\rm K}$ in the burned gas, where the latter represents the adiabatic flame temperature. The outermost flamelets represent the unstretched flamelet (dotted black curve) and the conditions when extinction occurs (yellow curve), e.g. defined by a rapid reduction of reaction rates if strain rate is further increased. In figure 4(b), the joint p.d.f. is compared with a set of unstretched premixed flamelets with different equivalence ratios, ranging from ![]() $\phi =0.34$ to
$\phi =0.34$ to ![]() $\phi =1.0$, where the former is close to the flammability limit. It is evident that the strained flamelets can only parametrize a small portion of the entire flame state, while the set of unstretched flamelets covers almost the entire joint p.d.f. except for a small region of low mixture fraction and high progress variable values. However, extrapolation into this region does not pose any significant challenges as the source term of progress variable is close to zero due to the low mixture fraction values. Thus, the set of unstretched flamelets is used for modelling, as already proposed by Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013).
$\phi =1.0$, where the former is close to the flammability limit. It is evident that the strained flamelets can only parametrize a small portion of the entire flame state, while the set of unstretched flamelets covers almost the entire joint p.d.f. except for a small region of low mixture fraction and high progress variable values. However, extrapolation into this region does not pose any significant challenges as the source term of progress variable is close to zero due to the low mixture fraction values. Thus, the set of unstretched flamelets is used for modelling, as already proposed by Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013).

Figure 4. Joint p.d.f. of progress variable and mixture fraction in the turbulent flame (a) overlaid by strained flamelets with different strain rates ![]() $a$ obtained from a premixed counterflow flame and (b) overlaid by unstretched flamelets with different equivalence ratios
$a$ obtained from a premixed counterflow flame and (b) overlaid by unstretched flamelets with different equivalence ratios ![]() $\phi$.
$\phi$.
Since the set of unstretched flamelets does not feature any overlaps, building a table to predict ![]() $\dot {\omega }_{H_2}(C_{H_2},Z)$ is straightforward. A comparison of the table prediction
$\dot {\omega }_{H_2}(C_{H_2},Z)$ is straightforward. A comparison of the table prediction ![]() $\dot {\omega }_{H_2}^{FL}$ and the conditional average
$\dot {\omega }_{H_2}^{FL}$ and the conditional average ![]() $\langle \dot {\omega }_{H_2} \mid C_{H_2},Z \rangle$ of the DNS data is shown in figure 5. While certain differences are seen in regions with high mixture fractions, which are characterized by high values of curvature, good qualitative agreement is observed overall and, in particular, at flame states of high probability, cf. figure 4. As will be shown quantitatively below in figure 12, low modelling errors are achieved with this model.
$\langle \dot {\omega }_{H_2} \mid C_{H_2},Z \rangle$ of the DNS data is shown in figure 5. While certain differences are seen in regions with high mixture fractions, which are characterized by high values of curvature, good qualitative agreement is observed overall and, in particular, at flame states of high probability, cf. figure 4. As will be shown quantitatively below in figure 12, low modelling errors are achieved with this model.

Figure 5. (a) Conditionally averaged progress variable source term with respect to mixture fraction and progress variable and (b) model prediction of progress variable source by the set of unstretched premixed flamelets.
Analogously, a model based on the water-based progress variable can be built for the instantaneous source term ![]() $\dot {\omega }_{H_2O}$, yielding similarly good agreement with the DNS data and is discussed at the end of this section.
$\dot {\omega }_{H_2O}$, yielding similarly good agreement with the DNS data and is discussed at the end of this section.
4.2.2. Modelling the subfilter p.d.f.
For LES, a model for the subfilter p.d.f. ![]() $\tilde {\mathcal {P}}(C_{H_2},Z)$ or
$\tilde {\mathcal {P}}(C_{H_2},Z)$ or ![]() $\tilde {\mathcal {P}}(C_{H_2O},Z)$ is required. The joint p.d.f. of the hydrogen-based progress variable and mixture fraction is shown in figure 4, while the p.d.f. with a water-based progress variable is shown in figure 6. Comparing the two p.d.f.s, a distinct difference is evident: in contrast to the hydrogen-based progress variable, the water-based progress variable features super-equilibrium values in the burned gas, e.g.
$\tilde {\mathcal {P}}(C_{H_2O},Z)$ is required. The joint p.d.f. of the hydrogen-based progress variable and mixture fraction is shown in figure 4, while the p.d.f. with a water-based progress variable is shown in figure 6. Comparing the two p.d.f.s, a distinct difference is evident: in contrast to the hydrogen-based progress variable, the water-based progress variable features super-equilibrium values in the burned gas, e.g. ![]() $C_{H_2O} > 1$. In particular,
$C_{H_2O} > 1$. In particular, ![]() $C_{H_2O}$ behaves similar to the temperature field, which features super-adiabatic values, cf. figure 1. Thus,
$C_{H_2O}$ behaves similar to the temperature field, which features super-adiabatic values, cf. figure 1. Thus, ![]() $C_{H_2O}$ is not bounded like the hydrogen-based progress variable with
$C_{H_2O}$ is not bounded like the hydrogen-based progress variable with ![]() $C_{H_2} \in [0,1]$. This makes a formulation of a p.d.f. for
$C_{H_2} \in [0,1]$. This makes a formulation of a p.d.f. for ![]() $C_{H_2O}$ challenging, so in the following, a presumed subfilter p.d.f. is only suggested for the hydrogen-based progress variable. However, a model for the water-based progress variable can be also formulated using the presumed subfilter p.d.f. for the hydrogen-based progress variable as discussed in the next section.
$C_{H_2O}$ challenging, so in the following, a presumed subfilter p.d.f. is only suggested for the hydrogen-based progress variable. However, a model for the water-based progress variable can be also formulated using the presumed subfilter p.d.f. for the hydrogen-based progress variable as discussed in the next section.
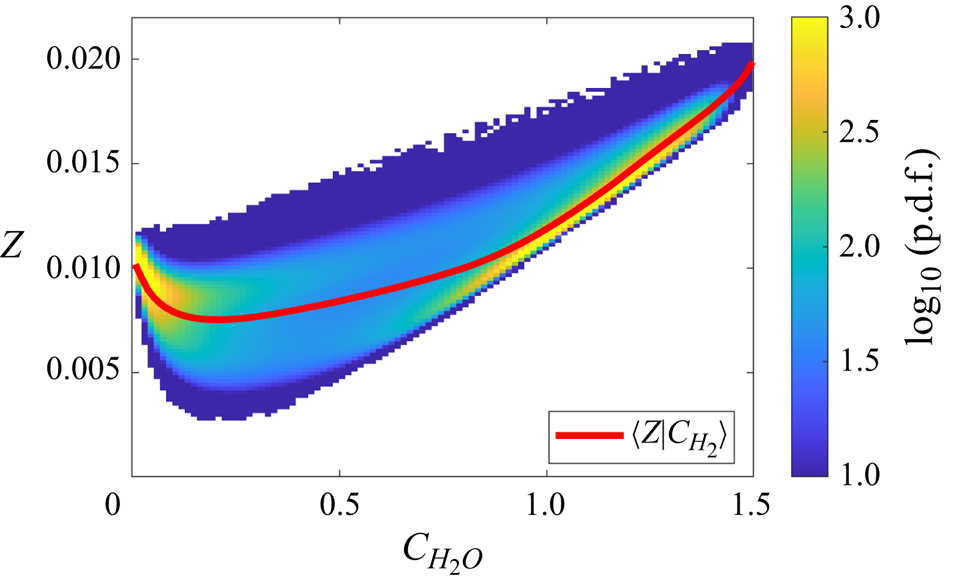
Figure 6. Joint p.d.f. of progress variable ![]() $C_{H_2O}$ and mixture fraction
$C_{H_2O}$ and mixture fraction ![]() $Z$ in the turbulent flame.
$Z$ in the turbulent flame.
It is evident from figure 4 that progress variable and mixture fraction are not independent. This effect is also reflected by the strongly curved trajectories of the unstretched flamelets in figure 4(b), which feature a local minimum of mixture fraction for intermediate progress variable values. To transform mixture fraction and progress variable into a set of independent variables, which significantly simplifies the modelling of ![]() $\tilde {\mathcal {P}}(C_{H_2},Z)$, the joint p.d.f. of progress variable and a flamelet index is investigated. The latter is the value of the nominal equivalence ratio
$\tilde {\mathcal {P}}(C_{H_2},Z)$, the joint p.d.f. of progress variable and a flamelet index is investigated. The latter is the value of the nominal equivalence ratio ![]() $\phi ^{FL}$ for each unstretched flamelet in figure 4(b) and, hence, is constant within a flamelet. Thus, in contrast to mixture fraction,
$\phi ^{FL}$ for each unstretched flamelet in figure 4(b) and, hence, is constant within a flamelet. Thus, in contrast to mixture fraction, ![]() $\phi ^{FL}$ is independent of progress variable. To determine
$\phi ^{FL}$ is independent of progress variable. To determine ![]() $\phi ^{FL}$ locally from mixture fraction and progress variable, the flamelet index
$\phi ^{FL}$ locally from mixture fraction and progress variable, the flamelet index ![]() $\phi ^{FL}$ is tabulated as a function of these two parameters analogously to the source term in the previous section. Then,
$\phi ^{FL}$ is tabulated as a function of these two parameters analogously to the source term in the previous section. Then, ![]() $\phi ^{FL}$ can be computed for each DNS data point and the joint p.d.f. of progress variable and the flame index is shown in figure 7. Conveniently,
$\phi ^{FL}$ can be computed for each DNS data point and the joint p.d.f. of progress variable and the flame index is shown in figure 7. Conveniently, ![]() $\phi ^{FL}$ and
$\phi ^{FL}$ and ![]() $C_{H_2}$ are statistically almost independent. To highlight this aspect, figure 7 also shows the joint distribution of the local equivalence ratio
$C_{H_2}$ are statistically almost independent. To highlight this aspect, figure 7 also shows the joint distribution of the local equivalence ratio ![]() $\phi$ of the DNS, which is determined as (Peters Reference Peters2000)
$\phi$ of the DNS, which is determined as (Peters Reference Peters2000)
and contains the same information as mixture fraction. Here, ![]() $Z_{st}$ indicates the stoichiometric value of mixture fraction, which is
$Z_{st}$ indicates the stoichiometric value of mixture fraction, which is ![]() $Z_{st}=0.028$. Note that
$Z_{st}=0.028$. Note that ![]() $\phi$ is different from the flamelet index
$\phi$ is different from the flamelet index ![]() $\phi ^{FL}$, as
$\phi ^{FL}$, as ![]() $\phi$ represents the local composition while
$\phi$ represents the local composition while ![]() $\phi ^{FL}$ indicates the nominal equivalence ratio in the unburned gas that corresponds to the local composition. For instance, from figure 4(b), it is evident that mixture fraction and the local composition within a flamelet vary due to differential diffusion effects, but
$\phi ^{FL}$ indicates the nominal equivalence ratio in the unburned gas that corresponds to the local composition. For instance, from figure 4(b), it is evident that mixture fraction and the local composition within a flamelet vary due to differential diffusion effects, but ![]() $\phi ^{FL}$ is constant for a flamelet by definition. Comparing the two distributions
$\phi ^{FL}$ is constant for a flamelet by definition. Comparing the two distributions ![]() $\mathcal {P}(C_{H_2},\phi ^{FL})$ and
$\mathcal {P}(C_{H_2},\phi ^{FL})$ and ![]() $\mathcal {P}(C_{H_2},\phi )$ in figure 7, a significantly stronger correlation between
$\mathcal {P}(C_{H_2},\phi )$ in figure 7, a significantly stronger correlation between ![]() $\phi$ and progress variable
$\phi$ and progress variable ![]() $C_{H_2}$ is seen. This is further emphasized in figure 8, where the two joint distributions
$C_{H_2}$ is seen. This is further emphasized in figure 8, where the two joint distributions ![]() $\mathcal {P}(C_{H_2}=C_0,\phi ^{FL})$ and
$\mathcal {P}(C_{H_2}=C_0,\phi ^{FL})$ and ![]() $\mathcal {P}(C_{H_2}=C_0,\phi )$ are shown for constant values of progress variable
$\mathcal {P}(C_{H_2}=C_0,\phi )$ are shown for constant values of progress variable ![]() $C_0$. It is evident that the distribution
$C_0$. It is evident that the distribution ![]() $\mathcal {P}(C_{H_2},\phi )$ strongly varies with progress variable, e.g. a shifting of the peak is seen. In contrast, the distribution
$\mathcal {P}(C_{H_2},\phi )$ strongly varies with progress variable, e.g. a shifting of the peak is seen. In contrast, the distribution ![]() $\mathcal {P}(C_{H_2}, \phi ^{FL})$ is less sensitive to the value of progress variable, e.g. the peak and width of the distribution are similar for all progress variable values. Further, it is interesting to note that the conditional average of the flamelet index
$\mathcal {P}(C_{H_2}, \phi ^{FL})$ is less sensitive to the value of progress variable, e.g. the peak and width of the distribution are similar for all progress variable values. Further, it is interesting to note that the conditional average of the flamelet index ![]() $\langle \phi ^{FL} \mid C_{H_2} \rangle$ lies within the flame above the nominal equivalence ratio of
$\langle \phi ^{FL} \mid C_{H_2} \rangle$ lies within the flame above the nominal equivalence ratio of ![]() $\phi =0.4$. This indicates that, on average, combustion occurs on a richer flamelet of
$\phi =0.4$. This indicates that, on average, combustion occurs on a richer flamelet of ![]() $\phi ^{FL} \approx 0.5$, which is consistent with the analysis of Berger et al. (Reference Berger, Attili and Pitsch2022b), who showed that combustion occurs at richer mixtures due to the mean positive strain rate universally observed in turbulent flows (Rutland & Trouvé Reference Rutland and Trouvé1993; Luca et al. Reference Luca, Al-Khateeb, Attili and Bisetti2018; Chu et al. Reference Chu, Berger, Gauding, Attili and Pitsch2024).
$\phi ^{FL} \approx 0.5$, which is consistent with the analysis of Berger et al. (Reference Berger, Attili and Pitsch2022b), who showed that combustion occurs at richer mixtures due to the mean positive strain rate universally observed in turbulent flows (Rutland & Trouvé Reference Rutland and Trouvé1993; Luca et al. Reference Luca, Al-Khateeb, Attili and Bisetti2018; Chu et al. Reference Chu, Berger, Gauding, Attili and Pitsch2024).

Figure 7. Comparison of (a) joint distribution of progress variable and local equivalence ratio and (b) the joint distribution of progress variable and the flamelet index.

Figure 8. (a) Joint distribution of progress variable and local equivalence ratio and (b) joint distribution of progress variable and the flamelet index evaluated at constant values of progress variable.
Assuming statistical independence of ![]() $\phi ^{FL}$ and
$\phi ^{FL}$ and ![]() $C_{H_2}$, and similar to the model of Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), a model for the presumed p.d.f. is proposed,
$C_{H_2}$, and similar to the model of Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), a model for the presumed p.d.f. is proposed,
Similar to previous works (Galpin et al. Reference Galpin, Naudin, Vervisch, Angelberger, Colin and Domingo2008; Vreman et al. Reference Vreman, van Oijen, de Goey and Bastiaans2009; Pfitzner Reference Pfitzner2021), a ![]() $\beta$-p.d.f. is assumed for
$\beta$-p.d.f. is assumed for ![]() $C_{H_2}$ and a
$C_{H_2}$ and a ![]() $\delta$-p.d.f. is assumed for the flamelet index
$\delta$-p.d.f. is assumed for the flamelet index ![]() $\phi ^{FL}$. The
$\phi ^{FL}$. The ![]() $\delta$-p.d.f. implies that the combustion process locally occurs on an unstretched flamelet with an equivalence ratio of
$\delta$-p.d.f. implies that the combustion process locally occurs on an unstretched flamelet with an equivalence ratio of ![]() $\tilde {\phi }^{FL}$, where
$\tilde {\phi }^{FL}$, where ![]() $\tilde {\phi }^{FL}=\tilde {\phi }^{FL}(\tilde {C}_{H_2}, \widetilde {{C_{H_2}^{{''}^2}}}, \tilde {Z})$ varies with the local values of the filtered progress variable, the progress variable variance and mixture fraction. Further note that the assumption of an
$\tilde {\phi }^{FL}=\tilde {\phi }^{FL}(\tilde {C}_{H_2}, \widetilde {{C_{H_2}^{{''}^2}}}, \tilde {Z})$ varies with the local values of the filtered progress variable, the progress variable variance and mixture fraction. Further note that the assumption of an ![]() $\beta$-p.d.f. for
$\beta$-p.d.f. for ![]() $C_{H_2}$ is possible, as
$C_{H_2}$ is possible, as ![]() $C_{H_2}$ is strictly bound to
$C_{H_2}$ is strictly bound to ![]() $C_{H_2} \in [0,1]$. For the water-based progress variable, a
$C_{H_2} \in [0,1]$. For the water-based progress variable, a ![]() $\beta$-p.d.f. cannot be assumed due to the super-unity values of
$\beta$-p.d.f. cannot be assumed due to the super-unity values of ![]() $C_{H_2O}$. Note that if using the formulation of a hydrogen-based progress variable and mixture fraction, the information of the super-equilibrium regions in the post-flame region, where
$C_{H_2O}$. Note that if using the formulation of a hydrogen-based progress variable and mixture fraction, the information of the super-equilibrium regions in the post-flame region, where ![]() $C_{H_2}=1$, is provided by mixture fraction.
$C_{H_2}=1$, is provided by mixture fraction.
Using (4.8), the filtered source term can be expressed as
 \begin{align} &= \bar{\rho} \int \frac{\dot{\omega}_{H_2}(C_{H_2},\tilde{\phi}^{FL})}{\rho(C_{H_2},\tilde{\phi}^{FL})} \beta(C_{H_2}) \,\text{d}C_{H_2} . \end{align}
\begin{align} &= \bar{\rho} \int \frac{\dot{\omega}_{H_2}(C_{H_2},\tilde{\phi}^{FL})}{\rho(C_{H_2},\tilde{\phi}^{FL})} \beta(C_{H_2}) \,\text{d}C_{H_2} . \end{align}
Note that this integral depends on ![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ and
$\widetilde {{C_{H_2}^{{''}^2}}}$ and ![]() $\tilde {Z}$ since the
$\tilde {Z}$ since the ![]() $\beta$-p.d.f. is parametrized by
$\beta$-p.d.f. is parametrized by ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$, and
$\widetilde {{C_{H_2}^{{''}^2}}}$, and ![]() $\tilde {\phi }^{FL}$ is implicitly determined by
$\tilde {\phi }^{FL}$ is implicitly determined by ![]() $\tilde {Z}$. The latter is given by
$\tilde {Z}$. The latter is given by
Thus, to determine ![]() $\tilde {\phi }^{FL}$ for the computation of
$\tilde {\phi }^{FL}$ for the computation of ![]() $\bar {\dot {\omega }}_{H_2}$ in (4.10), the integral for the filtered mixture fraction in (4.11) is computed for all different flamelets, and the value
$\bar {\dot {\omega }}_{H_2}$ in (4.10), the integral for the filtered mixture fraction in (4.11) is computed for all different flamelets, and the value ![]() $\tilde {\phi }^{FL}$ is given by the flamelet that matches the value of
$\tilde {\phi }^{FL}$ is given by the flamelet that matches the value of ![]() $\tilde {Z}$ at a given value of
$\tilde {Z}$ at a given value of ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$.
$\widetilde {{C_{H_2}^{{''}^2}}}$.
In practice, a table can be built directly as a function of ![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\tilde {Z}$ and
$\tilde {Z}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$. For this, (4.10) and (4.11) are evaluated for each flamelet for a grid of
$\widetilde {{C_{H_2}^{{''}^2}}}$. For this, (4.10) and (4.11) are evaluated for each flamelet for a grid of ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ values. Here, a linear spacing is used for
$\widetilde {{C_{H_2}^{{''}^2}}}$ values. Here, a linear spacing is used for ![]() $\widetilde {C_{H_2}}$ and a quadratic spacing for
$\widetilde {C_{H_2}}$ and a quadratic spacing for ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ to enhance the table resolution for small values. Since
$\widetilde {{C_{H_2}^{{''}^2}}}$ to enhance the table resolution for small values. Since ![]() $\tilde {Z}$ monotonically increases with
$\tilde {Z}$ monotonically increases with ![]() $\tilde {\phi }^{FL}$, the data can be interpolated from the (
$\tilde {\phi }^{FL}$, the data can be interpolated from the (![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$,
$\widetilde {{C_{H_2}^{{''}^2}}}$, ![]() $\tilde {\phi }^{FL}$)-space to the (
$\tilde {\phi }^{FL}$)-space to the (![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$,
$\widetilde {{C_{H_2}^{{''}^2}}}$, ![]() $\tilde {Z}$)-space.
$\tilde {Z}$)-space.
Figure 9 shows three panels of the tabulated value of ![]() $\bar {\dot {\omega }}_{H_2}$, where either
$\bar {\dot {\omega }}_{H_2}$, where either ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ or
$\widetilde {{C_{H_2}^{{''}^2}}}$ or ![]() $\tilde {Z}$ are kept constant. In figure 9(a), the table is evaluated at zero progress variable variance and, hence, corresponds to the tabulated unfiltered source term. In figure 9(b), the same plot is shown at
$\tilde {Z}$ are kept constant. In figure 9(a), the table is evaluated at zero progress variable variance and, hence, corresponds to the tabulated unfiltered source term. In figure 9(b), the same plot is shown at ![]() $\widetilde {{C_{H_2}^{{''}^2}}}=0.1$. As expected, the source term magnitude reduces with increasing progress variable variance if comparing with panel (a). The same trend can be seen in figure 9(c), where the variation of the source term with progress variable variance is explicitly shown for a fixed value of mixture fraction. Further note that in an LES, the relevant range of the table is given by the constraint
$\widetilde {{C_{H_2}^{{''}^2}}}=0.1$. As expected, the source term magnitude reduces with increasing progress variable variance if comparing with panel (a). The same trend can be seen in figure 9(c), where the variation of the source term with progress variable variance is explicitly shown for a fixed value of mixture fraction. Further note that in an LES, the relevant range of the table is given by the constraint ![]() $\widetilde {{C_{H_2}^{{''}^2}}}<\tilde {C}_{H_2}(1-\tilde {C}_{H_2})$. This represents the maximum possible progress variable variance. However, for numerical stability, the table is extrapolated to the entire parametric space, e.g. by setting the value of any lookup scalar in the extrapolated region to the value at
$\widetilde {{C_{H_2}^{{''}^2}}}<\tilde {C}_{H_2}(1-\tilde {C}_{H_2})$. This represents the maximum possible progress variable variance. However, for numerical stability, the table is extrapolated to the entire parametric space, e.g. by setting the value of any lookup scalar in the extrapolated region to the value at ![]() $\widetilde {{C_{H_2}^{{''}^2}}}=\tilde {C}_{H_2}(1-\tilde {C}_{H_2})$. Similarly, the table is extrapolated in the direction of mixture fraction, the physical region of which is bound towards lower values by the flamelet solution with the lowest equivalence ratio.
$\widetilde {{C_{H_2}^{{''}^2}}}=\tilde {C}_{H_2}(1-\tilde {C}_{H_2})$. Similarly, the table is extrapolated in the direction of mixture fraction, the physical region of which is bound towards lower values by the flamelet solution with the lowest equivalence ratio.
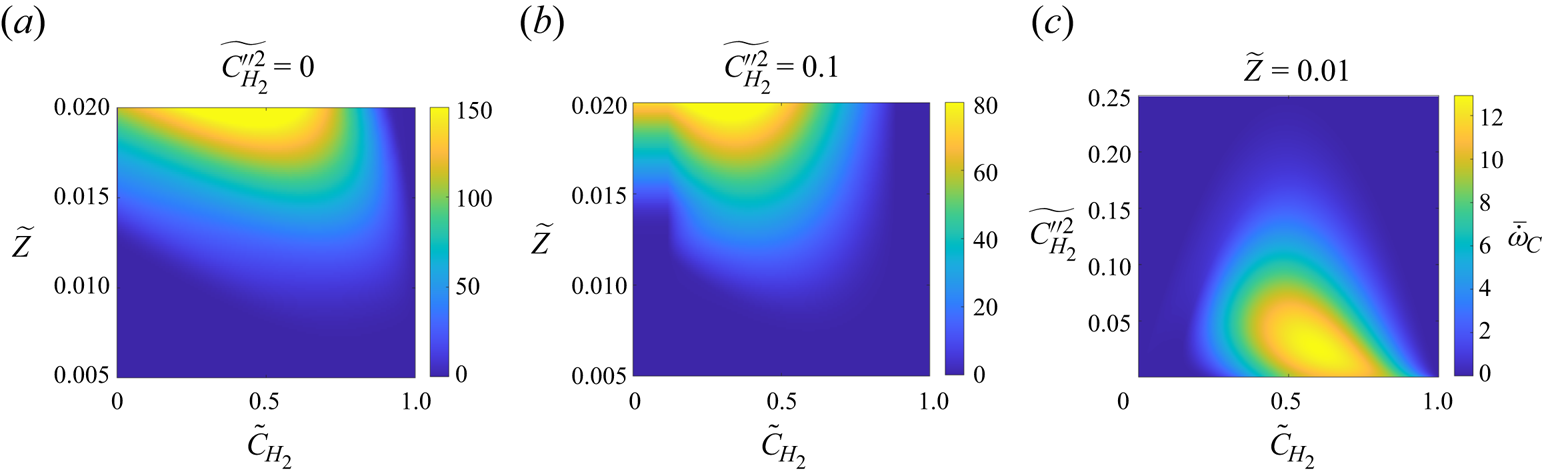
Figure 9. Lookup table prediction of ![]() $\bar {\dot {\omega }}_{H_2}$ as function of the filtered parameters (
$\bar {\dot {\omega }}_{H_2}$ as function of the filtered parameters (![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$,
$\widetilde {{C_{H_2}^{{''}^2}}}$, ![]() $\tilde {Z}$) for (a,b) two particular values of
$\tilde {Z}$) for (a,b) two particular values of ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ and (c) one for a constant value of
$\widetilde {{C_{H_2}^{{''}^2}}}$ and (c) one for a constant value of ![]() $\tilde {Z}$.
$\tilde {Z}$.
4.2.3. Lookup-table based on water-based progress variable
For modelling unclosed filtered terms, a presumed subfilter p.d.f. has been introduced in previous sections. The subfilter p.d.f. was formulated only for the hydrogen-based progress variable as an analogous formulation is not possible for a water-based progress variable due to the super-equilibrium values of ![]() $C_{H_2O}$, which cannot be represented by a
$C_{H_2O}$, which cannot be represented by a ![]() $\beta$-p.d.f. for
$\beta$-p.d.f. for ![]() $C_{H_2O}$. Thus, to model unclosed filtered terms with a water-based progress variable, a different approach is followed. In particular, no presumed p.d.f. is explicitly formulated for
$C_{H_2O}$. Thus, to model unclosed filtered terms with a water-based progress variable, a different approach is followed. In particular, no presumed p.d.f. is explicitly formulated for ![]() $C_{H_2O}$, but the previously introduced, well-posed presumed p.d.f. for
$C_{H_2O}$, but the previously introduced, well-posed presumed p.d.f. for ![]() $C_{H_2}$ is used. First, the values of
$C_{H_2}$ is used. First, the values of ![]() $\widetilde {C_{H_2O}}$ and
$\widetilde {C_{H_2O}}$ and ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ are determined with the
$\widetilde {{C_{H_2O}^{{''}^2}}}$ are determined with the ![]() $C_{H_2}$-based model. These values are computed for each unstretched flamelet
$C_{H_2}$-based model. These values are computed for each unstretched flamelet ![]() $\phi ^{FL}$ on a pre-specified grid of
$\phi ^{FL}$ on a pre-specified grid of ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ as
$\widetilde {{C_{H_2}^{{''}^2}}}$ as
where ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ is determined from
$\widetilde {{C_{H_2O}^{{''}^2}}}$ is determined from ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}=\widetilde {{C_{H_2O}}^2}-\widetilde {C_{H_2O}}^2$. It is worth noting that in (4.12) and (4.13), the instantaneous values of
$\widetilde {{C_{H_2O}^{{''}^2}}}=\widetilde {{C_{H_2O}}^2}-\widetilde {C_{H_2O}}^2$. It is worth noting that in (4.12) and (4.13), the instantaneous values of ![]() $C_{H_2O}$ are determined from the unstretched flamelet manifold that is parametrized by
$C_{H_2O}$ are determined from the unstretched flamelet manifold that is parametrized by ![]() $C_{H_2}$ and
$C_{H_2}$ and ![]() $\phi ^{FL}$. Thus,
$\phi ^{FL}$. Thus, ![]() $C_{H_2O}$ is looked up analogously to other quantities, such as
$C_{H_2O}$ is looked up analogously to other quantities, such as ![]() $\rho$ or
$\rho$ or ![]() $\dot {\omega }_{H_2}$, as a function of
$\dot {\omega }_{H_2}$, as a function of ![]() $C_{H_2}$. Similarly, the filtered progress variable source term
$C_{H_2}$. Similarly, the filtered progress variable source term ![]() $\bar {\dot {\omega }}_{H_2O}$ of
$\bar {\dot {\omega }}_{H_2O}$ of ![]() $C_{H_2O}$ is computed for each flamelet as
$C_{H_2O}$ is computed for each flamelet as
Since the flame state can be uniquely mapped from the (![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$)-space to the (
$\widetilde {{C_{H_2}^{{''}^2}}}$)-space to the (![]() $\widetilde {C_{H_2O}}$,
$\widetilde {C_{H_2O}}$, ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$)-space for each flamelet, the filtered source term can be unambiguously expressed as a function of
$\widetilde {{C_{H_2O}^{{''}^2}}}$)-space for each flamelet, the filtered source term can be unambiguously expressed as a function of ![]() $\widetilde {C_{H_2O}}$ and
$\widetilde {C_{H_2O}}$ and ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$. For each flamelet, this relationship can be determined by computing the conditional mean
$\widetilde {{C_{H_2O}^{{''}^2}}}$. For each flamelet, this relationship can be determined by computing the conditional mean
The notation ![]() $\langle \cdots \rangle _{\tilde {\phi }^{FL}}$ denotes that the mapping procedure from
$\langle \cdots \rangle _{\tilde {\phi }^{FL}}$ denotes that the mapping procedure from ![]() $[\widetilde {C_{H_2}}, \widetilde {{C_{H_2}^{{''}^2}}}]$ to
$[\widetilde {C_{H_2}}, \widetilde {{C_{H_2}^{{''}^2}}}]$ to ![]() $[\widetilde {C_{H_2O}}, \widetilde {{C_{H_2O}^{{''}^2}}}]$ is performed for each flamelet
$[\widetilde {C_{H_2O}}, \widetilde {{C_{H_2O}^{{''}^2}}}]$ is performed for each flamelet ![]() $\tilde {\phi }^{FL}$ separately. Figure 10 shows the mapping for the particular flamelet with
$\tilde {\phi }^{FL}$ separately. Figure 10 shows the mapping for the particular flamelet with ![]() $\tilde {\phi }^{FL}=0.4$. The visible data points are linked to the pre-specified discretization of the table based on
$\tilde {\phi }^{FL}=0.4$. The visible data points are linked to the pre-specified discretization of the table based on ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$. Due to the unique mapping, the scatter becomes a well-defined manifold and an unambiguous determination of
$\widetilde {{C_{H_2}^{{''}^2}}}$. Due to the unique mapping, the scatter becomes a well-defined manifold and an unambiguous determination of ![]() $\bar {\dot {\omega }}_{H_2O}$ as a function of
$\bar {\dot {\omega }}_{H_2O}$ as a function of ![]() $\widetilde {C_{H_2O}}$ and
$\widetilde {C_{H_2O}}$ and ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ is possible.
$\widetilde {{C_{H_2O}^{{''}^2}}}$ is possible.

Figure 10. Mapping from the hydrogen-based to water-based combustion model formulation for the flamelet with ![]() $\tilde{\phi}^{FL}=0.4$. Scatter of filtered source term
$\tilde{\phi}^{FL}=0.4$. Scatter of filtered source term ![]() $\bar {\dot {\omega }}_{H_2O}$ from table lookup as a function of filtered progress variable
$\bar {\dot {\omega }}_{H_2O}$ from table lookup as a function of filtered progress variable ![]() $\widetilde {C_{H_2O}}$ and progress variable variance
$\widetilde {C_{H_2O}}$ and progress variable variance ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$.
$\widetilde {{C_{H_2O}^{{''}^2}}}$.
Finally, the data are mapped from the (![]() $\widetilde {C_{H_2O}}$,
$\widetilde {C_{H_2O}}$, ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$,
$\widetilde {{C_{H_2O}^{{''}^2}}}$, ![]() $\tilde {\phi }^{FL}$)-space to the (
$\tilde {\phi }^{FL}$)-space to the (![]() $\widetilde {C_{H_2O}}$,
$\widetilde {C_{H_2O}}$, ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$,
$\widetilde {{C_{H_2O}^{{''}^2}}}$, ![]() $\tilde {Z}$)-space, where
$\tilde {Z}$)-space, where ![]() $\tilde {Z}$ is computed according to (4.11). The resulting table is shown in figure 11 for two different values of
$\tilde {Z}$ is computed according to (4.11). The resulting table is shown in figure 11 for two different values of ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ and at constant mixture fraction. The characteristic super-equilibrium regions (
$\widetilde {{C_{H_2O}^{{''}^2}}}$ and at constant mixture fraction. The characteristic super-equilibrium regions (![]() $\widetilde {C_{H_2O}}>1$) are well recovered with this approach. Additionally, it is worth noting that for large mixture fraction values featuring local equivalence ratios with
$\widetilde {C_{H_2O}}>1$) are well recovered with this approach. Additionally, it is worth noting that for large mixture fraction values featuring local equivalence ratios with ![]() $\phi ^{FL}>0.4$, the hydrogen mass fraction in the unburned state, defined by
$\phi ^{FL}>0.4$, the hydrogen mass fraction in the unburned state, defined by ![]() $\widetilde {C_{H_2O}}=0$, is larger than the hydrogen mass fraction
$\widetilde {C_{H_2O}}=0$, is larger than the hydrogen mass fraction ![]() $Y_{H_2,u}$ in the unburned gas in the DNS. Such regions cannot be parametrized with a hydrogen-based progress variable
$Y_{H_2,u}$ in the unburned gas in the DNS. Such regions cannot be parametrized with a hydrogen-based progress variable ![]() $C_{H_2} \in [0,1]$ and can also not occur in the DNS, so table entries in these regions represent only an extrapolation for numerical stability.
$C_{H_2} \in [0,1]$ and can also not occur in the DNS, so table entries in these regions represent only an extrapolation for numerical stability.

Figure 11. Look-up table prediction of ![]() $\bar {\dot {\omega }}_{H_2O}$ as function of the filtered input parameters (
$\bar {\dot {\omega }}_{H_2O}$ as function of the filtered input parameters (![]() $\widetilde {C_{H_2O}}$,
$\widetilde {C_{H_2O}}$, ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$,
$\widetilde {{C_{H_2O}^{{''}^2}}}$, ![]() $\tilde {Z}$) for (a,b) two particular values of
$\tilde {Z}$) for (a,b) two particular values of ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ and (c) one for a constant value of
$\widetilde {{C_{H_2O}^{{''}^2}}}$ and (c) one for a constant value of ![]() $\tilde {Z}$.
$\tilde {Z}$.
4.3. Assessment of source term model
Figure 12 shows the assessment of four different combustion models for three different filter sizes. The following models are considered for the comparison:
(i) model
 $\phi =0.4$-Fl. uses a single flamelet at the nominal equivalence ratio, neglecting the effects of a subfilter p.d.f. and the fluctuations of mixture fraction;
$\phi =0.4$-Fl. uses a single flamelet at the nominal equivalence ratio, neglecting the effects of a subfilter p.d.f. and the fluctuations of mixture fraction;(ii) model
 $\phi =0.4$-Fl.+p.d.f. uses a single flamelet at the nominal equivalence ratio and while it neglects the fluctuations of mixture fraction, it considers the effects of a subfilter distribution by a presumed
$\phi =0.4$-Fl.+p.d.f. uses a single flamelet at the nominal equivalence ratio and while it neglects the fluctuations of mixture fraction, it considers the effects of a subfilter distribution by a presumed  $\beta$-p.d.f. for progress variable. This is a common model for turbulent premixed flames of conventional fuels when thermodiffusive instabilities are not present (Pfitzner Reference Pfitzner2021);
$\beta$-p.d.f. for progress variable. This is a common model for turbulent premixed flames of conventional fuels when thermodiffusive instabilities are not present (Pfitzner Reference Pfitzner2021);(iii) model
 $\phi$-Var. describes the local mixture fraction fluctuations by a series of unstretched premixed flamelets with varying equivalence ratio according to Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013). However, the effects of the subfilter distribution are neglected; and
$\phi$-Var. describes the local mixture fraction fluctuations by a series of unstretched premixed flamelets with varying equivalence ratio according to Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013). However, the effects of the subfilter distribution are neglected; and(iv) model
 $\phi$-Var.+p.d.f. is the model described in the previous section and additionally considers the presumed p.d.f. of (4.8) to account for the complex subfilter fluctuations of mixture fraction and progress variable.
$\phi$-Var.+p.d.f. is the model described in the previous section and additionally considers the presumed p.d.f. of (4.8) to account for the complex subfilter fluctuations of mixture fraction and progress variable.

Figure 12. Model assessment for ![]() $\bar {\dot {\omega }}_{H_2}$ using a hydrogen-based progress variable. Modelling errors of the progress variable source term for three different filter sizes (a)
$\bar {\dot {\omega }}_{H_2}$ using a hydrogen-based progress variable. Modelling errors of the progress variable source term for three different filter sizes (a) ![]() $\varDelta = 0$, (b)
$\varDelta = 0$, (b) ![]() $\varDelta =l_{F}$ and (c)
$\varDelta =l_{F}$ and (c) ![]() $\varDelta =2 l_{F}$ for the four different flamelet-based models.
$\varDelta =2 l_{F}$ for the four different flamelet-based models.
Figure 12 shows the conditionally averaged modelling error as a function of progress variable. The modelling error is defined as
where the same normalization as for the irreducible errors is chosen. This definition compares the absolute modelling errors with the maximum average progress variable source term within the flame. Note that the value of the normalization is constant for one particular filter size but decreases for increasing filter size, as filtering reduces the maximum value of the progress variable source term.
For the unfiltered DNS data, a significant reduction of modelling errors is observed by the flamelet manifold model ![]() $\phi$-Var. with respect to the single-flamelet model
$\phi$-Var. with respect to the single-flamelet model ![]() $\phi =0.4$-Fl., which neglects the effects of differential diffusion and yields an average deviation larger than 100 % of the filtered source term value within the DNS. In contrast, the modelling errors for the
$\phi =0.4$-Fl., which neglects the effects of differential diffusion and yields an average deviation larger than 100 % of the filtered source term value within the DNS. In contrast, the modelling errors for the ![]() $\phi$-Var. model are almost zero, indicating an accurate representation of the flame state by the series of unstretched premixed flamelets. In particular, the maximum value of the conditional mean modelling errors in figure 12 drops from 1.53 for the
$\phi$-Var. model are almost zero, indicating an accurate representation of the flame state by the series of unstretched premixed flamelets. In particular, the maximum value of the conditional mean modelling errors in figure 12 drops from 1.53 for the ![]() $\phi =0.4$-Fl. model to 0.032 for the
$\phi =0.4$-Fl. model to 0.032 for the ![]() $\phi$-Var. model. For the filtered fields, the single-flamelet model
$\phi$-Var. model. For the filtered fields, the single-flamelet model ![]() $\phi =0.4$-Fl. again shows high modelling errors, which does not significantly change for the
$\phi =0.4$-Fl. again shows high modelling errors, which does not significantly change for the ![]() $\phi =0.4$-Fl.+p.d.f. model that additionally considers a subfilter distribution. These two models entirely neglect the effects of local mixture fraction fluctuations, so their failure is expected. It is worth noting that a value of unity indicates a significant error, as the modelling errors are as large as the maximum value of the conditionally averaged progress variable source term. Further, the modelling errors of model
$\phi =0.4$-Fl.+p.d.f. model that additionally considers a subfilter distribution. These two models entirely neglect the effects of local mixture fraction fluctuations, so their failure is expected. It is worth noting that a value of unity indicates a significant error, as the modelling errors are as large as the maximum value of the conditionally averaged progress variable source term. Further, the modelling errors of model ![]() $\phi$-Var. are seen to increase with increasing filter size. This results from a strong overprediction of the progress variable source term by the model, as it does not consider the effect of filtering. In particular, filtering leads to a reduction of the peak reaction rates. In contrast, the newly proposed model
$\phi$-Var. are seen to increase with increasing filter size. This results from a strong overprediction of the progress variable source term by the model, as it does not consider the effect of filtering. In particular, filtering leads to a reduction of the peak reaction rates. In contrast, the newly proposed model ![]() $\phi$-Var.+p.d.f., which accounts for the effects of a subfilter distribution by means of the presumed p.d.f. in (4.8), yields a significant reduction of modelling errors, leading to maximum modelling errors below 0.11 for both filter sizes, as shown in Appendix B.
$\phi$-Var.+p.d.f., which accounts for the effects of a subfilter distribution by means of the presumed p.d.f. in (4.8), yields a significant reduction of modelling errors, leading to maximum modelling errors below 0.11 for both filter sizes, as shown in Appendix B.
For the source term model based on the water-based progress variable, as discussed in § 4.2.3, figure 13 shows the a priori modelling errors for ![]() $\dot {\omega }_{H_2O}$ for three different filter sizes. Large errors are observed for the models
$\dot {\omega }_{H_2O}$ for three different filter sizes. Large errors are observed for the models ![]() $\phi =0.4$-Fl. and
$\phi =0.4$-Fl. and ![]() $\phi =0.4$-Fl.+p.d.f. as differential diffusion effects are not considered. A significant reduction of modelling errors is only observed if using the flamelet-manifold model in conjunction with the presumed subfilter p.d.f. However, comparing with figure 12, the hydrogen-based formulation of the flamelet-manifold model with subfilter p.d.f. appears to yield lower a priori modelling errors than the water-based model variant.
$\phi =0.4$-Fl.+p.d.f. as differential diffusion effects are not considered. A significant reduction of modelling errors is only observed if using the flamelet-manifold model in conjunction with the presumed subfilter p.d.f. However, comparing with figure 12, the hydrogen-based formulation of the flamelet-manifold model with subfilter p.d.f. appears to yield lower a priori modelling errors than the water-based model variant.

Figure 13. Model assessment for ![]() $\bar {\dot {\omega }}_{H_2O}$ using a water-based progress variable. Modelling errors of the progress variable source term for three different filter sizes (a)
$\bar {\dot {\omega }}_{H_2O}$ using a water-based progress variable. Modelling errors of the progress variable source term for three different filter sizes (a) ![]() $\varDelta = 0$, (b)
$\varDelta = 0$, (b) ![]() $\varDelta =l_{F}$ and (c)
$\varDelta =l_{F}$ and (c) ![]() $\varDelta =2 l_{F}$ for the four different flamelet-based models.
$\varDelta =2 l_{F}$ for the four different flamelet-based models.
To highlight the good model prediction of the ![]() $\phi =0.4$-Fl.+p.d.f. model for flames, where differential diffusion effects are not present, figure 14 shows the modelling errors of the
$\phi =0.4$-Fl.+p.d.f. model for flames, where differential diffusion effects are not present, figure 14 shows the modelling errors of the ![]() $\phi =0.4$-Fl. and
$\phi =0.4$-Fl. and ![]() $\phi =0.4$-Fl.+p.d.f. models if evaluated for the DNS case of Berger et al. (Reference Berger, Attili and Pitsch2022b), where differential diffusion effects have been artificially suppressed. For the unfiltered field, the single-flamelet model yields a good representation of the DNS as there is only moderate impact of turbulence on the flame, e.g. due to turbulent strain rate and curvature, cf. also the discussion by Berger et al. (Reference Berger, Attili and Pitsch2022b). It is also evident that for an increasing filter size, the consideration of a
$\phi =0.4$-Fl.+p.d.f. models if evaluated for the DNS case of Berger et al. (Reference Berger, Attili and Pitsch2022b), where differential diffusion effects have been artificially suppressed. For the unfiltered field, the single-flamelet model yields a good representation of the DNS as there is only moderate impact of turbulence on the flame, e.g. due to turbulent strain rate and curvature, cf. also the discussion by Berger et al. (Reference Berger, Attili and Pitsch2022b). It is also evident that for an increasing filter size, the consideration of a ![]() $\beta$-distribution for the subfilter p.d.f. is a good assumption that leads to negligibly small modelling errors. This analysis highlights that the failure of the
$\beta$-distribution for the subfilter p.d.f. is a good assumption that leads to negligibly small modelling errors. This analysis highlights that the failure of the ![]() $\phi =0.4$-Fl.+p.d.f. model in figure 12 for the DNS case, which features strong differential diffusion effects, is specifically linked to the presence of thermodiffusive effects and differential diffusion.
$\phi =0.4$-Fl.+p.d.f. model in figure 12 for the DNS case, which features strong differential diffusion effects, is specifically linked to the presence of thermodiffusive effects and differential diffusion.

Figure 14. Model assessment for ![]() $\bar {\dot {\omega }}_{H_2O}$ using a water-based progress variable for the TurbStable DNS that does not feature differential diffusion effects. Only the
$\bar {\dot {\omega }}_{H_2O}$ using a water-based progress variable for the TurbStable DNS that does not feature differential diffusion effects. Only the ![]() $\phi =0.4$-Fl. and
$\phi =0.4$-Fl. and ![]() $\phi =0.4$-Fl.+p.d.f. models are considered.
$\phi =0.4$-Fl.+p.d.f. models are considered.
4.4. Model for progress variable variance
The lookup tables require the variance of progress variable as an input. Hence, an algebraic correlation or transport equation for ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ or
$\widetilde {{C_{H_2}^{{''}^2}}}$ or ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ is needed. As will be shown in detail,
$\widetilde {{C_{H_2O}^{{''}^2}}}$ is needed. As will be shown in detail, ![]() $\widetilde {{C_{i}^{{''}^2}}}$ is found to be well parametrized by progress variable
$\widetilde {{C_{i}^{{''}^2}}}$ is found to be well parametrized by progress variable ![]() $\widetilde {C_{i}}$, mixture fraction
$\widetilde {C_{i}}$, mixture fraction ![]() $\tilde {Z}$ and the magnitude of the gradient of progress variable
$\tilde {Z}$ and the magnitude of the gradient of progress variable ![]() $| \boldsymbol {\nabla } \widetilde {C_{i}} |$. Thus, in this work, a data-driven model based on the DNS data is employed for
$| \boldsymbol {\nabla } \widetilde {C_{i}} |$. Thus, in this work, a data-driven model based on the DNS data is employed for ![]() $\widetilde {{C_{i}^{{''}^2}}}$ to allow for a rigorous analysis of the LES as errors linked to the modelling of
$\widetilde {{C_{i}^{{''}^2}}}$ to allow for a rigorous analysis of the LES as errors linked to the modelling of ![]() $\widetilde {{C_{i}^{{''}^2}}}$ can be ruled out. However, note that such a model may not be applicable to other conditions and flame configurations, as it is specific to the present DNS case. In the following, the modelling of
$\widetilde {{C_{i}^{{''}^2}}}$ can be ruled out. However, note that such a model may not be applicable to other conditions and flame configurations, as it is specific to the present DNS case. In the following, the modelling of ![]() $\widetilde {{C_{i}^{{''}^2}}}$ based on the DNS data is discussed.
$\widetilde {{C_{i}^{{''}^2}}}$ based on the DNS data is discussed.
For an a priori analysis of filtered quantities, first, an appropriate filter size needs to be chosen. However, this is not known a priori and may even vary within an LES due to different local conditions. For instance, filtering the DNS data with large filter sizes leads to low gradients of the filtered fields, so the local gradient information in the LES may be regarded as a measure of the local filter size. Since a model for ![]() $\widetilde {{C_{i}^{{''}^2}}}$ should be valid at different filter sizes and the filter size is not known a priori, the DNS data are filtered at several different filter sizes, ranging from
$\widetilde {{C_{i}^{{''}^2}}}$ should be valid at different filter sizes and the filter size is not known a priori, the DNS data are filtered at several different filter sizes, ranging from ![]() $\varDelta =3\delta _{DNS}$ to
$\varDelta =3\delta _{DNS}$ to ![]() $\varDelta =40\delta _{DNS}$, where
$\varDelta =40\delta _{DNS}$, where ![]() $\delta _{DNS}=70~{\rm \mu} {\rm m}$ is the spatial discretization of the DNS data. To avoid limitations arising from a too narrow range of considered filter sizes, the range of filter sizes is chosen sufficiently large. The data are then used to perform an optimal estimator analysis to identify suitable parameters for modelling
$\delta _{DNS}=70~{\rm \mu} {\rm m}$ is the spatial discretization of the DNS data. To avoid limitations arising from a too narrow range of considered filter sizes, the range of filter sizes is chosen sufficiently large. The data are then used to perform an optimal estimator analysis to identify suitable parameters for modelling ![]() $\widetilde {{C_{i}^{{''}^2}}}$ across different filter sizes. For the optimal estimator analysis, the following variables are considered: the filtered progress variable and mixture fraction, and the gradient of the filtered progress variable. The former two parameters indicate the local flame state, while the gradient of the filtered progress variable is expected to parametrize the effect of different filter sizes.
$\widetilde {{C_{i}^{{''}^2}}}$ across different filter sizes. For the optimal estimator analysis, the following variables are considered: the filtered progress variable and mixture fraction, and the gradient of the filtered progress variable. The former two parameters indicate the local flame state, while the gradient of the filtered progress variable is expected to parametrize the effect of different filter sizes.
Figure 15 shows the irreducible errors for the parametrization of ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ with different sets of parameters. The irreducible errors are defined as
$\widetilde {{C_{H_2}^{{''}^2}}}$ with different sets of parameters. The irreducible errors are defined as
 \begin{equation} \epsilon^2_{{irr}} = \frac{ \left(\widetilde{{C_{H_2}^{{''}^2}}} - \left\langle \widetilde{{C_{H_2}^{{''}^2}}} \mid \boldsymbol{\psi} \right\rangle\right)^2}{\max\left[\left\langle \widetilde{{C_{H_2}^{{''}^2}}} \mid C_{H_2} \right\rangle\right]}, \end{equation}
\begin{equation} \epsilon^2_{{irr}} = \frac{ \left(\widetilde{{C_{H_2}^{{''}^2}}} - \left\langle \widetilde{{C_{H_2}^{{''}^2}}} \mid \boldsymbol{\psi} \right\rangle\right)^2}{\max\left[\left\langle \widetilde{{C_{H_2}^{{''}^2}}} \mid C_{H_2} \right\rangle\right]}, \end{equation}
where ![]() $\boldsymbol {\psi }$ represents the set of parameters considered for the optimal estimator analysis. The irreducible errors are normalized with the maximum value of the conditional mean variance
$\boldsymbol {\psi }$ represents the set of parameters considered for the optimal estimator analysis. The irreducible errors are normalized with the maximum value of the conditional mean variance ![]() $\langle \widetilde {{C_{H_2}^{{''}^2}}} \mid C_{H_2} \rangle$ in the DNS. Note that in this analysis, conditional averaging, denoted by
$\langle \widetilde {{C_{H_2}^{{''}^2}}} \mid C_{H_2} \rangle$ in the DNS. Note that in this analysis, conditional averaging, denoted by ![]() $\langle \rangle$, is performed for the ensemble of data that includes all considered filter sizes. High irreducible errors are observed if only using progress variable, while a significant reduction is achieved if using all three parameters. It is worth noting that if performing the optimal estimator analysis only for one particular filter size, a very good parametrization is already achieved using
$\langle \rangle$, is performed for the ensemble of data that includes all considered filter sizes. High irreducible errors are observed if only using progress variable, while a significant reduction is achieved if using all three parameters. It is worth noting that if performing the optimal estimator analysis only for one particular filter size, a very good parametrization is already achieved using ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $\tilde {Z}$. However, the filter size is not known a priori and figure 15 indicates that if using data with different filter sizes,
$\tilde {Z}$. However, the filter size is not known a priori and figure 15 indicates that if using data with different filter sizes, ![]() $| \boldsymbol {\nabla } \tilde {C}_{H_2}|$ is also needed for an adequate parametrization. To visualize the good parametrization of
$| \boldsymbol {\nabla } \tilde {C}_{H_2}|$ is also needed for an adequate parametrization. To visualize the good parametrization of ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ with
$\widetilde {{C_{H_2}^{{''}^2}}}$ with ![]() $\widetilde {C_{H_2}}$,
$\widetilde {C_{H_2}}$, ![]() $\tilde {Z}$ and
$\tilde {Z}$ and ![]() $| \boldsymbol {\nabla } \widetilde {C_{H_2}}|$, figure 16 shows the scatter of
$| \boldsymbol {\nabla } \widetilde {C_{H_2}}|$, figure 16 shows the scatter of ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ with respect to
$\widetilde {{C_{H_2}^{{''}^2}}}$ with respect to ![]() $\widetilde {C_{H_2}}$ and
$\widetilde {C_{H_2}}$ and ![]() $| \boldsymbol {\nabla } \widetilde {C_{H_2}}|$ at a given value of
$| \boldsymbol {\nabla } \widetilde {C_{H_2}}|$ at a given value of ![]() $\tilde {Z}$ for filtered data at various filter sizes. It is seen that the scatter aligns on a low-dimensional manifold. Thus, in the LES, the progress variable variance
$\tilde {Z}$ for filtered data at various filter sizes. It is seen that the scatter aligns on a low-dimensional manifold. Thus, in the LES, the progress variable variance ![]() $\widetilde {{C_{H_2}^{{''}^2}}}$ is modelled by the following conditional average based on the DNS data:
$\widetilde {{C_{H_2}^{{''}^2}}}$ is modelled by the following conditional average based on the DNS data:

Figure 15. Parametrization of the progress variable variance considering filtered DNS data with different filter sizes: irreducible errors for four different sets of parameters.

Figure 16. Parametrization of the progress variable variance: scattered filtered DNS data at different filter sizes for a given value of mixture fraction.
For the water-based progress variable, an analogous model is formulated and a similar good parametrization of ![]() $\widetilde {{C_{H_2O}^{{''}^2}}}$ by
$\widetilde {{C_{H_2O}^{{''}^2}}}$ by ![]() $\widetilde {C_{H_2O}}$,
$\widetilde {C_{H_2O}}$, ![]() $\tilde {Z}$ and
$\tilde {Z}$ and ![]() $| \boldsymbol {\nabla } \widetilde {C_{H_2O}}|$ is found.
$| \boldsymbol {\nabla } \widetilde {C_{H_2O}}|$ is found.
5. A posteriori analysis
In this section, the previously introduced models for the filtered progress variable source term are assessed in an a posteriori analysis. For this, several LES of the DNS of Berger et al. (Reference Berger, Attili and Pitsch2022b) are performed, solving the filtered (2.13) and (2.14) for progress variable and mixture fraction considering the different model variants.
5.1. LES configuration
The computational domain of the DNS of Berger et al. (Reference Berger, Attili and Pitsch2022b) is considered for the LES and a detailed description can be found from Berger et al. (Reference Berger, Attili and Pitsch2022b). The domain is periodic in the spanwise direction (![]() $z$), open boundary conditions are prescribed at the outlet in streamwise direction (
$z$), open boundary conditions are prescribed at the outlet in streamwise direction (![]() $x$) and slip conditions are imposed at the boundaries in cross-wise direction (
$x$) and slip conditions are imposed at the boundaries in cross-wise direction (![]() $y$). The inlet velocities of the central jet are taken from an auxiliary fully developed turbulent channel flow simulation and the same boundary conditions as in the DNS are applied (e.g. no filtered turbulent channel is computed). Laminar coflows are applied outside of the central jet, featuring a uniform velocity, which is set to 15 % of the bulk velocity
$y$). The inlet velocities of the central jet are taken from an auxiliary fully developed turbulent channel flow simulation and the same boundary conditions as in the DNS are applied (e.g. no filtered turbulent channel is computed). Laminar coflows are applied outside of the central jet, featuring a uniform velocity, which is set to 15 % of the bulk velocity ![]() $U$ of the central jet. An overview of the simulation parameters of the DNS of Berger et al. (Reference Berger, Attili and Pitsch2022b) and the LES of this work can be found in tables 1 and 2, respectively. Note that the LES domains are larger in axial direction compared with the DNS as longer flames are obtained in the LES.
$U$ of the central jet. An overview of the simulation parameters of the DNS of Berger et al. (Reference Berger, Attili and Pitsch2022b) and the LES of this work can be found in tables 1 and 2, respectively. Note that the LES domains are larger in axial direction compared with the DNS as longer flames are obtained in the LES.
Table 2. Simulation parameters of the DNS, which corresponds to the TurbUnstable case of Berger et al. (Reference Berger, Attili and Pitsch2022b), and the different LES of this work: slot width ![]() $H$ and bulk velocity
$H$ and bulk velocity ![]() $U$ of central jet inflow; velocity
$U$ of central jet inflow; velocity ![]() $U_{Coflow}$ of laminar coflow; grid resolution
$U_{Coflow}$ of laminar coflow; grid resolution ![]() $\varDelta$; domain size
$\varDelta$; domain size ![]() $L_{i}$; number of grid points
$L_{i}$; number of grid points ![]() $N_{i}$ in each direction; and jet Reynolds number
$N_{i}$ in each direction; and jet Reynolds number ![]() $Re$.
$Re$.

5.2. Governing equations and numerical methods
The flow is modelled by the filtered Navier–Stokes equations in the low-Mach-number limit (Tomboulides, Lee & Orszag Reference Tomboulides, Lee and Orszag1997) and the fluid is assumed to be an ideal gas. The subfilter-stress term in the momentum equation is closed by a dynamic Smagorinsky model (Pierce & Moin Reference Pierce and Moin1998) that uses Lagrangian averaging (Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). Due to the low-Mach-number formulation, a Poisson equation is solved for the pressure that enforces mass conservation. Further details can be found from Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013). For a rigorous assessment of the combustion model, four different formulations are investigated a posteriori in this work, which are referred to as C-model, C-Z-model(H ![]() $_2$O), C-Z-model(H
$_2$O), C-Z-model(H ![]() $_2$) and Finitechem LES; an overview of the models is given in table 3.
$_2$) and Finitechem LES; an overview of the models is given in table 3.
Table 3. Comparison of LES combustion models: parametrization of local flame state and subfilter closure. Note that the presumed p.d.f. for the two models C-Z-model(H ![]() $_2$) and C-Z-model(H
$_2$) and C-Z-model(H ![]() $_2$O) is identical, cf. (4.10) and (4.14). In the Finitechem LES model, transport equations for all species of the detailed chemical reaction mechanism of Burke et al. (Reference Burke, Chaos, Ju, Dryer and Klippenstein2012) are solved.
$_2$O) is identical, cf. (4.10) and (4.14). In the Finitechem LES model, transport equations for all species of the detailed chemical reaction mechanism of Burke et al. (Reference Burke, Chaos, Ju, Dryer and Klippenstein2012) are solved.

The C-model only solves the filtered transport equations of the water-based progress variable. Rather than using a manifold of flamelets with different equivalence ratio, the lookup table is created from one single unstretched premixed flamelet with a nominal equivalence ratio of ![]() $\phi =0.4$, which corresponds to the value of unburned mixture in the DNS. The C-Z-model(H
$\phi =0.4$, which corresponds to the value of unburned mixture in the DNS. The C-Z-model(H ![]() $_2$O) and C-Z-model(H
$_2$O) and C-Z-model(H ![]() $_2$) solve the filtered transport equations of progress variable and mixture fraction in (2.13) and (2.14), where the former uses the formulation with a water-based progress variable and the latter employs a hydrogen-based progress variable. These two models represent the previously introduced new models that represent the combustion process with a manifold of unstretched flamelets of different equivalence ratio and model the subfilter fluctuations via a presumed p.d.f. In all of these three models, the fluid properties, such as density, viscosity, diffusion coefficients for molecular diffusion and the Soret effect, and the progress variable source term are computed from the lookup tables. The temperature field, needed to compute the terms related to the Soret effect, is also extracted from the same lookup tables. Finally, the Finitechem LES model uses a detailed chemical reaction mechanism (Burke et al. Reference Burke, Chaos, Ju, Dryer and Klippenstein2012), the same used in the DNS, and solves transport equations for all species. Details on this model are described by Berger et al. (Reference Berger, Attili and Pitsch2022b). This model does not consider any subfilter closure on purpose and simply represents an under resolved DNS. Thus, it allows to assess the relevance of subfilter modelling for the present flames. Analogously to Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), the subfilter scalar flux in all models is closed using a turbulent diffusivity computed from a dynamic Smagorinsky-type model (Pierce & Moin Reference Pierce and Moin1998).
$_2$) solve the filtered transport equations of progress variable and mixture fraction in (2.13) and (2.14), where the former uses the formulation with a water-based progress variable and the latter employs a hydrogen-based progress variable. These two models represent the previously introduced new models that represent the combustion process with a manifold of unstretched flamelets of different equivalence ratio and model the subfilter fluctuations via a presumed p.d.f. In all of these three models, the fluid properties, such as density, viscosity, diffusion coefficients for molecular diffusion and the Soret effect, and the progress variable source term are computed from the lookup tables. The temperature field, needed to compute the terms related to the Soret effect, is also extracted from the same lookup tables. Finally, the Finitechem LES model uses a detailed chemical reaction mechanism (Burke et al. Reference Burke, Chaos, Ju, Dryer and Klippenstein2012), the same used in the DNS, and solves transport equations for all species. Details on this model are described by Berger et al. (Reference Berger, Attili and Pitsch2022b). This model does not consider any subfilter closure on purpose and simply represents an under resolved DNS. Thus, it allows to assess the relevance of subfilter modelling for the present flames. Analogously to Knudsen et al. (Reference Knudsen, Kolla, Hawkes and Pitsch2013), the subfilter scalar flux in all models is closed using a turbulent diffusivity computed from a dynamic Smagorinsky-type model (Pierce & Moin Reference Pierce and Moin1998).
A semi-implicit finite difference code, based on the Crank–Nicolson time advancement scheme and an iterative predictor corrector scheme, is employed (Desjardins et al. Reference Desjardins, Blanquart, Balarac and Pitsch2008). Spatial and temporal staggering is used to increase accuracy and stability. The Poisson equation for the pressure is solved by the preconditioned conjugate gradient HYPRE solver (Falgout & Yang Reference Falgout and Yang2002). Momentum equations are discretized with a fourth-order scheme. In the species and temperature equations, the convective term is discretized with a fifth-order WENO scheme (Jiang & Shu Reference Jiang and Shu1996) and the diffusion operator is discretized with fourth-order central differences. The time integration of the chemical source terms employs a table lookup. Note that the numerical code for the LES is the same as for the DNS.
The mesh of the LES is equidistant in all directions and is eight times coarser compared with the mesh of the DNS. Thus, the grid spacing is roughly as large as the laminar unstretched premixed flame thickness, which is ![]() $l_{F}= 0.714\,\text {mm}$ if determined based on the maximum temperature gradient. The grid resolution is chosen as coarse as possible to challenge the subfilter models, while it still needs to be fine enough to resolve the mean flow in the LES. The time step is controlled by the Courant–Friedrichs–Lewy (CFL) condition based on the local velocities and a maximum CFL number of 0.5 is allowed. Further, the maximum time step is limited to
$l_{F}= 0.714\,\text {mm}$ if determined based on the maximum temperature gradient. The grid resolution is chosen as coarse as possible to challenge the subfilter models, while it still needs to be fine enough to resolve the mean flow in the LES. The time step is controlled by the Courant–Friedrichs–Lewy (CFL) condition based on the local velocities and a maximum CFL number of 0.5 is allowed. Further, the maximum time step is limited to ![]() $\Delta t = 1\,\mathrm {\mu }{{\rm s}}$ in the LES to ensure an accurate time integration of the chemical reactions. The LES are run for at least four flow through times
$\Delta t = 1\,\mathrm {\mu }{{\rm s}}$ in the LES to ensure an accurate time integration of the chemical reactions. The LES are run for at least four flow through times ![]() $t_{Flow}$, defined by the ratio of domain length
$t_{Flow}$, defined by the ratio of domain length ![]() $L_{x}$ and bulk velocity
$L_{x}$ and bulk velocity ![]() $U$ as
$U$ as ![]() $t_{Flow} = L_{x}/U$, and statistics are collected after a statistically steady state is reached.
$t_{Flow} = L_{x}/U$, and statistics are collected after a statistically steady state is reached.
5.3. LES results and model assessment
Figure 17 shows a snapshot of all LES that have been performed for the TurbUnstable DNS case of Berger et al. (Reference Berger, Attili and Pitsch2022b) that features thermodiffusive instabilities. In addition to the four different combustion models, the filtered DNS is also shown for comparison. Note that the filter size ![]() $\varDelta$, used to filter the DNS, is not equal to the LES grid, but is chosen as
$\varDelta$, used to filter the DNS, is not equal to the LES grid, but is chosen as ![]() $\varDelta = 17 \delta _{DNS}$ as solving the filtered transport equations in LES leads to an implicit filtering with an unknown filter size a priori. The filter size is chosen such that the LES can be compared with a filtered field with similar local flame thickness and scalar gradients, which is further discussed in the following. From figure 17, significant differences among the different LES combustion models are evident. The C-model yields a significantly longer flame compared with the other LES and the DNS, which is expected as it does not capture the effects of differential diffusion, which have been shown to have a leading order impact on the flame dynamics and reaction rates (Berger et al. Reference Berger, Attili and Pitsch2022b). For the same reason, this combustion model is also not capable of reproducing the characteristic super-adiabatic temperatures that result from differential diffusion effects (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). In contrast, all other combustion models feature super-adiabatic temperatures as they intrinsically capture differential diffusion effects, e.g. by transporting two scalars such as progress variable and mixture fraction for the C-Z-models and in the Finitechem LES-model, each species possesses a different diffusion coefficient. However, differences among these three models are evident, e.g. the Finitechem LES model yields a significantly longer flame and the super-adiabatic temperature regions in the shear layer that start at the nozzle and evolve in the burned gas are only very weakly visible compared with the two flames with the C-Z-model and the DNS.
$\varDelta = 17 \delta _{DNS}$ as solving the filtered transport equations in LES leads to an implicit filtering with an unknown filter size a priori. The filter size is chosen such that the LES can be compared with a filtered field with similar local flame thickness and scalar gradients, which is further discussed in the following. From figure 17, significant differences among the different LES combustion models are evident. The C-model yields a significantly longer flame compared with the other LES and the DNS, which is expected as it does not capture the effects of differential diffusion, which have been shown to have a leading order impact on the flame dynamics and reaction rates (Berger et al. Reference Berger, Attili and Pitsch2022b). For the same reason, this combustion model is also not capable of reproducing the characteristic super-adiabatic temperatures that result from differential diffusion effects (Giannakopoulos et al. Reference Giannakopoulos, Gatzoulis, Frouzakis, Matalon and Tomboulides2015). In contrast, all other combustion models feature super-adiabatic temperatures as they intrinsically capture differential diffusion effects, e.g. by transporting two scalars such as progress variable and mixture fraction for the C-Z-models and in the Finitechem LES-model, each species possesses a different diffusion coefficient. However, differences among these three models are evident, e.g. the Finitechem LES model yields a significantly longer flame and the super-adiabatic temperature regions in the shear layer that start at the nozzle and evolve in the burned gas are only very weakly visible compared with the two flames with the C-Z-model and the DNS.

Figure 17. Instantaneous snapshots of the temperature distribution for the different LES and the filtered DNS data.
To quantitatively highlight the difference in flame height, figure 18 shows the axial fuel flux ![]() $\mathcal {F}$ along the axial direction:
$\mathcal {F}$ along the axial direction:
where ![]() $\rho$ represents the gas density,
$\rho$ represents the gas density, ![]() $u$ the axial velocity,
$u$ the axial velocity, ![]() $Y_{H_2}$ is the mass fraction of hydrogen, and the operator
$Y_{H_2}$ is the mass fraction of hydrogen, and the operator ![]() $\langle \cdots \rangle _{z,t}$ represents averaging in the homogeneous
$\langle \cdots \rangle _{z,t}$ represents averaging in the homogeneous ![]() $z$-direction and in time. For convenience, the fuel flux is normalized by its value at the inlet.
$z$-direction and in time. For convenience, the fuel flux is normalized by its value at the inlet.

Figure 18. Fuel mass flux along axial direction (![]() $x$) for the different LES and the DNS.
$x$) for the different LES and the DNS.
From figure 18, a significantly different fuel consumption and, hence, flame length is evident among the different flames. Consistent with the flame images in figure 17, the LES with the C-model significantly overpredicts the flame length of the DNS. In contrast, the two LES with the C-Z-model approach the DNS in terms of fuel consumption and flame length sufficiently well even though slightly longer flames are obtained. Noteworthy, the Finitechem LES case yields a longer flame than the two cases with the C-Z-model, indicating that the missing subfilter modelling has a significant effect on the LES prediction.
Figure 19 shows profiles of the averaged values of the filtered temperature field ![]() $\langle \tilde {T} \rangle _{z,t}$ and its fluctuations
$\langle \tilde {T} \rangle _{z,t}$ and its fluctuations ![]() $\sigma _{T}$ at different heights above the burner for the different cases. The fluctuations are defined as
$\sigma _{T}$ at different heights above the burner for the different cases. The fluctuations are defined as
Note that ![]() $\sigma _{T}$ of the DNS is computed based on the filtered fields to allow for a direct comparison. Consistent with the fuel consumption and flame lengths in figure 18, different temperature profiles are observed at different heights above the burner with the DNS profiles approaching the burned state the fastest, e.g. at
$\sigma _{T}$ of the DNS is computed based on the filtered fields to allow for a direct comparison. Consistent with the fuel consumption and flame lengths in figure 18, different temperature profiles are observed at different heights above the burner with the DNS profiles approaching the burned state the fastest, e.g. at ![]() $x/H\approx 6$, the mean temperature is already close to the adiabatic flame temperature and only small fluctuations
$x/H\approx 6$, the mean temperature is already close to the adiabatic flame temperature and only small fluctuations ![]() $\sigma _{T}$ are visible. As already pointed out, temperature overshoots are not visible for the LES with the C-model and only weakly present for the Finitechem LES case. For instance, at
$\sigma _{T}$ are visible. As already pointed out, temperature overshoots are not visible for the LES with the C-model and only weakly present for the Finitechem LES case. For instance, at ![]() $x/H=1$, the Finitechem LES case yields
$x/H=1$, the Finitechem LES case yields ![]() $T_{max} = 1498\,{\rm K}$, which is 74 K lower compared with the overshoots in the DNS. However, differences are also observed among the two C-Z-models: the C-Z-model(H
$T_{max} = 1498\,{\rm K}$, which is 74 K lower compared with the overshoots in the DNS. However, differences are also observed among the two C-Z-models: the C-Z-model(H ![]() $_2$) features higher temperature overshoots with
$_2$) features higher temperature overshoots with ![]() $T_{max} = 1650\,{\rm K}$ at
$T_{max} = 1650\,{\rm K}$ at ![]() $x/H=1$ compared with the DNS with
$x/H=1$ compared with the DNS with ![]() $T_{max} = 1572\,{\rm K}$, while the temperature peak values of
$T_{max} = 1572\,{\rm K}$, while the temperature peak values of ![]() $T_{max} = 1593\,{\rm K}$ of the C-Z-model(
$T_{max} = 1593\,{\rm K}$ of the C-Z-model( ![]() $H_2O$) compare well with the DNS at
$H_2O$) compare well with the DNS at ![]() $x/H=1$. Further, the C-Z-model(
$x/H=1$. Further, the C-Z-model( ![]() $H_2$) features an earlier widening of the jet compared with the C-Z-model(
$H_2$) features an earlier widening of the jet compared with the C-Z-model( ![]() $H_2O$) model as visible from the wider temperature profile at
$H_2O$) model as visible from the wider temperature profile at ![]() $x/H = 3$ at
$x/H = 3$ at ![]() $\langle \tilde {T} \rangle _{z,t} \approx 1200\,{\rm K}$. Similar trends are visible from the temperature fluctuations, e.g. higher temperature fluctuations are observed for the C-Z-model(H
$\langle \tilde {T} \rangle _{z,t} \approx 1200\,{\rm K}$. Similar trends are visible from the temperature fluctuations, e.g. higher temperature fluctuations are observed for the C-Z-model(H ![]() $_2$) than for the C-Z-model(H
$_2$) than for the C-Z-model(H ![]() $_2$O), whereas the latter is close to the DNS values for
$_2$O), whereas the latter is close to the DNS values for ![]() $x/H\le 3$. The other two cases reveal significantly different fluctuation profiles due to the longer flames, e.g. the fluctuations monotonically increase for the C-model up to
$x/H\le 3$. The other two cases reveal significantly different fluctuation profiles due to the longer flames, e.g. the fluctuations monotonically increase for the C-model up to ![]() $x/H=10$ as the flame penetrates sufficiently far downstream in this case.
$x/H=10$ as the flame penetrates sufficiently far downstream in this case.

Figure 19. (a–d) Mean temperature profiles and ( f–h) temperature fluctuations along lateral direction (![]() $y$) at different heights above the burner for the different LES and DNS.
$y$) at different heights above the burner for the different LES and DNS.
Figure 18 indicates a significantly different fuel consumption of the different flames, which is directly linked to a different consumption speed ![]() $s_{c}$. The latter is defined as (Poinsot & Veynante Reference Poinsot and Veynante2005)
$s_{c}$. The latter is defined as (Poinsot & Veynante Reference Poinsot and Veynante2005)
Here, ![]() $Y_{H_2,u}$ and
$Y_{H_2,u}$ and ![]() $\rho _{u}$ are the hydrogen mass fraction and density in the unburned gas,
$\rho _{u}$ are the hydrogen mass fraction and density in the unburned gas, ![]() $\dot {\omega }_{H_2}$ represents the fuel consumption rate, and
$\dot {\omega }_{H_2}$ represents the fuel consumption rate, and ![]() $A_0$ refers to a reference flame surface area, which is the surface area of the Favre-averaged hydrogen mass fraction field. Due to the spatial inhomogeneity of the flow in the axial direction
$A_0$ refers to a reference flame surface area, which is the surface area of the Favre-averaged hydrogen mass fraction field. Due to the spatial inhomogeneity of the flow in the axial direction ![]() $x$, it is appropriate to define a local turbulent flame speed (Attili et al. Reference Attili, Stefano, Denker, Bisetti and Pitsch2020). Thus, the streamwise direction is divided into a number of equally sized volumes
$x$, it is appropriate to define a local turbulent flame speed (Attili et al. Reference Attili, Stefano, Denker, Bisetti and Pitsch2020). Thus, the streamwise direction is divided into a number of equally sized volumes ![]() $\mathcal {V}$ to evaluate the volumetric integral of the source term in (5.3). Each of these extends along the entire spanwise
$\mathcal {V}$ to evaluate the volumetric integral of the source term in (5.3). Each of these extends along the entire spanwise ![]() $z$ and cross-wise direction
$z$ and cross-wise direction ![]() $y$. The size of these volumes in the streamwise direction is as small as possible but finite such that converged statistics are obtained. It is worth noting that for the LES with the C-Z-model(
$y$. The size of these volumes in the streamwise direction is as small as possible but finite such that converged statistics are obtained. It is worth noting that for the LES with the C-Z-model( ![]() $H_2O$) and C-model, which use a water-based progress variable, a consumption speed could be similarly defined based on the water production rate
$H_2O$) and C-model, which use a water-based progress variable, a consumption speed could be similarly defined based on the water production rate ![]() $\dot {\omega }_{H_2O}$, but no significant differences are observed if using such a definition, so for simplicity, all simulations are compared according to (5.3). For the cases based on flamelet models, the source term
$\dot {\omega }_{H_2O}$, but no significant differences are observed if using such a definition, so for simplicity, all simulations are compared according to (5.3). For the cases based on flamelet models, the source term ![]() $\dot {\omega }_{H_2}$ is then determined from a table-lookup based on either
$\dot {\omega }_{H_2}$ is then determined from a table-lookup based on either ![]() $(\tilde {C}_{H_2},\widetilde {C^{''2}_{H_2}} , \tilde {Z} )$ or
$(\tilde {C}_{H_2},\widetilde {C^{''2}_{H_2}} , \tilde {Z} )$ or ![]() $(\tilde {C}_{H_2O},\widetilde {C^{''2}_{H_2O}} , \tilde {Z} )$. For the Finitechem LES case,
$(\tilde {C}_{H_2O},\widetilde {C^{''2}_{H_2O}} , \tilde {Z} )$. For the Finitechem LES case, ![]() $\dot {\omega }_{H_2}$ is evaluated with the detailed chemical mechanism without considering any subfilter model.
$\dot {\omega }_{H_2}$ is evaluated with the detailed chemical mechanism without considering any subfilter model.
Figure 20 shows the consumption speed of the different cases along the axial direction. Consistent with the fuel consumption, the DNS case features the highest fuel consumption, similar values are observed for the two C-Z-models, and the low fuel consumption rates of the Finitechem LES and C-model cases lead to significantly longer flames compared with the other cases. To further analyse this behaviour, the consumption speed is decomposed as
Here, ![]() $s_{L}$ is the laminar unstretched burning velocity, the ratio
$s_{L}$ is the laminar unstretched burning velocity, the ratio ![]() ${A}/{A_0}$ represents the effect of flame wrinkling on the turbulent flame speed, where
${A}/{A_0}$ represents the effect of flame wrinkling on the turbulent flame speed, where ![]() $A$ denotes the averaged turbulent flame surface area, and
$A$ denotes the averaged turbulent flame surface area, and ![]() $I_0$ is referred to as stretch factor and accounts for variations of the local reactivity from the unstretched laminar burning velocity and variations of the local flame thickness as introduced, e.g. by Bray (Reference Bray1990) and Bray & Cant (Reference Bray and Cant1991). To compute the averaged turbulent flame surface area, the instantaneous flame surface area
$I_0$ is referred to as stretch factor and accounts for variations of the local reactivity from the unstretched laminar burning velocity and variations of the local flame thickness as introduced, e.g. by Bray (Reference Bray1990) and Bray & Cant (Reference Bray and Cant1991). To compute the averaged turbulent flame surface area, the instantaneous flame surface area ![]() $A_{inst.}$ in each volume
$A_{inst.}$ in each volume ![]() $\mathcal {V}$ is determined from the hydrogen mass fraction according to Vervisch et al. (Reference Vervisch, Bidaux, Bray and Kollmann1995); technical details can be found from Berger et al. (Reference Berger, Attili and Pitsch2022b). Then,
$\mathcal {V}$ is determined from the hydrogen mass fraction according to Vervisch et al. (Reference Vervisch, Bidaux, Bray and Kollmann1995); technical details can be found from Berger et al. (Reference Berger, Attili and Pitsch2022b). Then, ![]() $A_{inst.}$ is averaged in time to yield
$A_{inst.}$ is averaged in time to yield ![]() $A$. It is worth noting that also for the C-Z-model(
$A$. It is worth noting that also for the C-Z-model( ![]() $H_2O$) and C-model, the flame surface area has been computed based on the hydrogen mass fraction field, which is determined from the look-up tables. This is important as the flame surface area determined from the water mass fraction field possesses spurious contributions due to long tails into the burned gas, cf. Berger et al. (Reference Berger, Attili and Pitsch2022a) and Howarth et al. (Reference Howarth, Hunt and Aspden2023). The stretch factor
$H_2O$) and C-model, the flame surface area has been computed based on the hydrogen mass fraction field, which is determined from the look-up tables. This is important as the flame surface area determined from the water mass fraction field possesses spurious contributions due to long tails into the burned gas, cf. Berger et al. (Reference Berger, Attili and Pitsch2022a) and Howarth et al. (Reference Howarth, Hunt and Aspden2023). The stretch factor ![]() $I_0$ is then computed from (5.4).
$I_0$ is then computed from (5.4).

Figure 20. Consumption speed of the different LES and the filtered DNS along the axial direction ![]() $x$.
$x$.
Figure 21 shows the increase of flame surface area along the axial direction for the different simulations. Consistent with the visual impression from figure 17, low flame wrinkling is seen for the C-model. Among the LES, the highest flame wrinkling is obtained in the C-Z-model( ![]() $H_2$), which visually also shows the most small-scale structures in figure 17, yielding similar flame wrinkling rates as in the filtered DNS. Figure 22 shows the stretch factor for all cases. For this, it is worth noting that the value of the filtered DNS (
$H_2$), which visually also shows the most small-scale structures in figure 17, yielding similar flame wrinkling rates as in the filtered DNS. Figure 22 shows the stretch factor for all cases. For this, it is worth noting that the value of the filtered DNS (![]() $I_0 \approx 6-5$), which is depicted in figure 22, is higher than the values of the unfiltered DNS (
$I_0 \approx 6-5$), which is depicted in figure 22, is higher than the values of the unfiltered DNS (![]() $I_0 \approx 5-4$, cf. Berger et al. Reference Berger, Attili and Pitsch2022b). This is a direct consequence of the filtering procedure: (i) filtering does not affect the consumption speed
$I_0 \approx 5-4$, cf. Berger et al. Reference Berger, Attili and Pitsch2022b). This is a direct consequence of the filtering procedure: (i) filtering does not affect the consumption speed ![]() $s_{c}$ as it only redistributes the local source term; (ii) filtering leads to a reduction of flame surface area. Thus, the effects of subfilter wrinkling are accounted for in the stretch factor. While none of the LES can reproduce the high stretch factors of the DNS, the C-Z-model(
$s_{c}$ as it only redistributes the local source term; (ii) filtering leads to a reduction of flame surface area. Thus, the effects of subfilter wrinkling are accounted for in the stretch factor. While none of the LES can reproduce the high stretch factors of the DNS, the C-Z-model( ![]() $H_2O$) approaches closest the DNS and yields the highest values among the LES cases. From figures 21 and 22, it is evident that while the two C-Z-models yield similar overall fuel consumption, the local flame dynamics differ among the two cases, e.g. the C-Z-model(
$H_2O$) approaches closest the DNS and yields the highest values among the LES cases. From figures 21 and 22, it is evident that while the two C-Z-models yield similar overall fuel consumption, the local flame dynamics differ among the two cases, e.g. the C-Z-model( ![]() $H_2$) features higher flame wrinkling and the C-Z-model(
$H_2$) features higher flame wrinkling and the C-Z-model( ![]() $H_2O$) features higher overall reaction rates. However, both cases show a significant enhancement of flame wrinkling and reaction rates compared with the C-model, which does not account for differential diffusion effects, indicating a significant impact of the proposed model on both contributions.
$H_2O$) features higher overall reaction rates. However, both cases show a significant enhancement of flame wrinkling and reaction rates compared with the C-model, which does not account for differential diffusion effects, indicating a significant impact of the proposed model on both contributions.

Figure 21. Flame surface area of the different LES and the filtered DNS along the axial direction ![]() $x$.
$x$.

Figure 22. Stretch factor of the different LES and the filtered DNS along the axial direction ![]() $x$.
$x$.
To understand the variations of the stretch factor, the local flame state is further investigated in figure 23, which shows the joint distribution among the hydrogen-based progress variable and mixture fraction. The C-model is not shown as it does not feature any effects of differential diffusion and, hence, mixture fraction fluctuations. Among the different LES, the conditional mean ![]() $\langle \tilde {Z} \mid \tilde {C}_{H_2} \rangle$ of the C-Z-model(
$\langle \tilde {Z} \mid \tilde {C}_{H_2} \rangle$ of the C-Z-model( ![]() $H_2O$) qualitatively resembles the filtered DNS best as the C-Z-model(
$H_2O$) qualitatively resembles the filtered DNS best as the C-Z-model( ![]() $H_2$) and Finitechem LES cases yield a strong overprediction compared with the filtered DNS at high progress variable values. Further, the narrow distribution of mixture fraction around the conditional mean in the Finitechem LES case indicates a reduced impact of differential diffusion effects in this case, which is consistent with the low super-adiabatic temperatures observed in figure 17. In contrast, significant mixture fraction fluctuations are visible for the C-Z-model(
$H_2$) and Finitechem LES cases yield a strong overprediction compared with the filtered DNS at high progress variable values. Further, the narrow distribution of mixture fraction around the conditional mean in the Finitechem LES case indicates a reduced impact of differential diffusion effects in this case, which is consistent with the low super-adiabatic temperatures observed in figure 17. In contrast, significant mixture fraction fluctuations are visible for the C-Z-model( ![]() $H_2$), which are even larger towards the burned gas than the fluctuations in the DNS and explain the higher super-adiabatic temperatures compared with the DNS in figure 17. The C-Z-model(
$H_2$), which are even larger towards the burned gas than the fluctuations in the DNS and explain the higher super-adiabatic temperatures compared with the DNS in figure 17. The C-Z-model( ![]() $H_2O$) represents an intermediate state, which features a sufficient widening of the joint distribution while extremal values of mixture fraction are similar to the DNS.
$H_2O$) represents an intermediate state, which features a sufficient widening of the joint distribution while extremal values of mixture fraction are similar to the DNS.

Figure 23. Local flame state in the LES and filtered DNS characterized by joint distribution of ![]() $\tilde {C}_{H_2}$ and
$\tilde {C}_{H_2}$ and ![]() $Z$. (a) Filtered DNS. (b) Finitechem LES. (c) C-Z-model(
$Z$. (a) Filtered DNS. (b) Finitechem LES. (c) C-Z-model(![]() ${\rm H}_2{\rm O}$). (d) C-Z-model(
${\rm H}_2{\rm O}$). (d) C-Z-model(![]() ${\rm H}_2$).
${\rm H}_2$).
As reaction rates sensitively depend on mixture fraction and progress variable, a good representation of the local flame state is critical. In figure 24, the conditional mean fuel consumption rate ![]() $\langle \bar {\dot {\omega }}_{H_2} \mid \tilde {C}_{H_2} \rangle$ is depicted for all cases. It is evident that the C-model features the lowest source term as it does not account for the effects of differential diffusion. Note that for the C-model and C-Z-model(
$\langle \bar {\dot {\omega }}_{H_2} \mid \tilde {C}_{H_2} \rangle$ is depicted for all cases. It is evident that the C-model features the lowest source term as it does not account for the effects of differential diffusion. Note that for the C-model and C-Z-model( ![]() $H_2O$), the values of
$H_2O$), the values of ![]() $\bar {\dot {\omega }}_{H_2}$ and
$\bar {\dot {\omega }}_{H_2}$ and ![]() $\tilde {C}_{H_2}$ are looked up as a function of
$\tilde {C}_{H_2}$ are looked up as a function of ![]() $\tilde {C}_{H_2O}$,
$\tilde {C}_{H_2O}$, ![]() $\widetilde {C^{''2}_{H_2O}}$ and
$\widetilde {C^{''2}_{H_2O}}$ and ![]() $\tilde {Z}$. All other LES tend to under predict the fuel consumption rate at low progress variable values, while they feature higher reaction rates towards the burned gas compared with the DNS. Both trends are linked to the joint distributions depicted in figure 23 as the DNS features the largest conditional mean mixture fraction values for small progress variable values, while the LES feature higher mixture fraction values towards the burned gas. However, to explain the differences in the stretch factor in figure 22, it is important to note that the source term is volumetrically integrated in (5.3). Thus, variations of the local flame thickness also affect the stretch factor. As flame thickness is directly linked to the local gradients within the flame, figure 25 shows the gradient of temperature conditionally averaged with respect to temperature for all LES and the filtered DNS. The filter size of the DNS has been chosen such that the magnitude of the maximum temperature gradient of the filtered field approximately matches the maximum values of the LES, or in other words, to match the implicit filter size characteristic of the LES field. Thus, note that a different filter size would lead to a different mean temperature gradient in figure 25 and conditionally averaged fuel consumption rate in figure 24. However, the particular filter size of
$\tilde {Z}$. All other LES tend to under predict the fuel consumption rate at low progress variable values, while they feature higher reaction rates towards the burned gas compared with the DNS. Both trends are linked to the joint distributions depicted in figure 23 as the DNS features the largest conditional mean mixture fraction values for small progress variable values, while the LES feature higher mixture fraction values towards the burned gas. However, to explain the differences in the stretch factor in figure 22, it is important to note that the source term is volumetrically integrated in (5.3). Thus, variations of the local flame thickness also affect the stretch factor. As flame thickness is directly linked to the local gradients within the flame, figure 25 shows the gradient of temperature conditionally averaged with respect to temperature for all LES and the filtered DNS. The filter size of the DNS has been chosen such that the magnitude of the maximum temperature gradient of the filtered field approximately matches the maximum values of the LES, or in other words, to match the implicit filter size characteristic of the LES field. Thus, note that a different filter size would lead to a different mean temperature gradient in figure 25 and conditionally averaged fuel consumption rate in figure 24. However, the particular filter size of ![]() $\varDelta = 17 \delta _{DNS}$ is chosen as the resulting temperature gradient and, hence, flame structure resembles the LES fields the closest for the comparison. The smallest gradients are observed for the C-model as a result of the small source term in figure 24. Further, the highest gradients among the LES are visible for the C-Z-model(
$\varDelta = 17 \delta _{DNS}$ is chosen as the resulting temperature gradient and, hence, flame structure resembles the LES fields the closest for the comparison. The smallest gradients are observed for the C-model as a result of the small source term in figure 24. Further, the highest gradients among the LES are visible for the C-Z-model( ![]() $H_2$), which explains the lower value of the volumetric integral and, hence, stretch factor compared with the C-Z-model(
$H_2$), which explains the lower value of the volumetric integral and, hence, stretch factor compared with the C-Z-model( ![]() $H_2O$) in figure 22. Most noteworthy, the DNS features a significant thickening of the mean flame front at low temperatures, which is not present in any LES. In conjunction with the relatively high reaction rates of the DNS for low progress variable values in figure 24, this leads to the high stretch factor values in figure 22.
$H_2O$) in figure 22. Most noteworthy, the DNS features a significant thickening of the mean flame front at low temperatures, which is not present in any LES. In conjunction with the relatively high reaction rates of the DNS for low progress variable values in figure 24, this leads to the high stretch factor values in figure 22.

Figure 24. Conditionally averaged source term ![]() $\bar {\dot {\omega }}_{H_2}$ with respect to
$\bar {\dot {\omega }}_{H_2}$ with respect to ![]() $\tilde {C}_{H_2}$ for all LES and the filtered DNS.
$\tilde {C}_{H_2}$ for all LES and the filtered DNS.

Figure 25. Conditionally averaged temperature gradients with respect to temperature for all cases.
5.4. LES results of jet flame without differential diffusion effects
Finally, an additional LES of the DNS of Berger et al. (Reference Berger, Attili and Pitsch2022b), where differential diffusion effects are artificially suppressed, has been performed. The computational set-up of this DNS features also a slot burner configuration and the operational conditions are the same in terms of jet Reynolds number, Karlovitz number, unburned temperature, equivalence ratio and pressure as those discussed in § 5.1. However, the Lewis numbers of all species have been set to unity and the Soret effect has been neglected to suppress differential diffusion effects; further technical details of the simulations are discussed by Berger et al. (Reference Berger, Attili and Pitsch2022b). Performing LES of this flame with the C-model allows an assessment of the capability of the employed modelling framework to predict turbulent jet flames. As no differential diffusion is present, good predictability of the C-model is expected. It is worth noting that the unstretched laminar flamelet used to generate the table for the C-model in this case has been also computed with unity Lewis numbers and no Soret effect to be consistent with the DNS.
Figure 26 shows two snapshots of the temperature field of the filtered DNS and LES. Analogously to the previous discussion, the filter size is chosen as ![]() $\varDelta = 17 \delta _{DNS}$ such that gradients in LES and filtered DNS are similar in magnitude. Additionally, figure 27 shows the fuel mass flux along the axial distance. Generally, good agreement of the filtered DNS and C-model is observed even though the flame length is overpredicted in the LES. In particular, the C-model overpredicts the flame length of the DNS without differential diffusion effects by approximately 25 %, while for the DNS with differential diffusion effects, the C-model yields a flame, which is approximately 270 % longer than the DNS. Here, the flame length is defined as the axial distance, where 99 % of the fuel is consumed, e.g. at
$\varDelta = 17 \delta _{DNS}$ such that gradients in LES and filtered DNS are similar in magnitude. Additionally, figure 27 shows the fuel mass flux along the axial distance. Generally, good agreement of the filtered DNS and C-model is observed even though the flame length is overpredicted in the LES. In particular, the C-model overpredicts the flame length of the DNS without differential diffusion effects by approximately 25 %, while for the DNS with differential diffusion effects, the C-model yields a flame, which is approximately 270 % longer than the DNS. Here, the flame length is defined as the axial distance, where 99 % of the fuel is consumed, e.g. at ![]() $\mathcal {F}=0.01$ in figures 18 and 27. This indicates that the employed modelling framework is suitable to predict turbulent premixed jet flames and the aforementioned discrepancies of the C-model to predict the DNS with strong thermodiffusive instabilities can be clearly linked to the fact that differential diffusion effects are not considered.
$\mathcal {F}=0.01$ in figures 18 and 27. This indicates that the employed modelling framework is suitable to predict turbulent premixed jet flames and the aforementioned discrepancies of the C-model to predict the DNS with strong thermodiffusive instabilities can be clearly linked to the fact that differential diffusion effects are not considered.

Figure 26. Instantaneous snapshots of the temperature fields for the TurbStable DNS without differential diffusion effects and the corresponding LES.

Figure 27. Fuel mass flux along axial direction (![]() $x$) for the TurbStable DNS without differential diffusion effects and the corresponding LES.
$x$) for the TurbStable DNS without differential diffusion effects and the corresponding LES.
6. Conclusions
In this work, an LES combustion model for premixed turbulent hydrogen flames has been developed and assessed a priori by means of DNS data and in an a posteriori analysis. In particular, the combustion model accounts for the effects of thermodiffusive instabilities, which have a leading order effect in hydrogen flames, and a new LES subfilter closure is proposed. The combustion model is based on progress variable and mixture fraction, and two different definitions of progress variable are tested in this work, using a water-based progress variable and a hydrogen-based progress variable.
In the first part, an a priori analysis is performed using DNS data. In an optimal estimator analysis of the DNS data, mixture fraction, progress variable and the variance of progress variable are identified as suitable parameters to adequately parametrize the fluctuations of the progress variable source term that are caused by thermodiffusive instabilities. Similar to previous work of Bastiaans et al. (Reference Bastiaans, Vreman and Pitsch2007) and Regele et al. (Reference Regele, Knudsen, Pitsch and Blanquart2013), the model is built on a set of unstretched premixed flamelets with different equivalence ratios, which is shown to accurately describe the instantaneous progress variable source term in the turbulent flame. To model the flame/turbulence subfilter interactions, a presumed p.d.f. based on progress variable and a flamelet index is proposed, where the latter describes the nominal equivalence ratio of a flamelet. The subfilter p.d.f. is modelled by a ![]() $\beta$-distribution for the progress variable and a
$\beta$-distribution for the progress variable and a ![]() $\delta$-distribution for the flamelet index. The latter assumes that combustion occurs within a subfilter volume along one particular flamelet, the equivalence ratio of which is chosen dynamically. An a priori assessment of the proposed LES combustion model indicates a significant reduction of modelling error in comparison to models that do not account for thermodiffusive instabilities and an adequate subfilter closure. While a hydrogen-based progress variable formulation is found to perform slightly better in the a priori analysis than the water-based progress variable, both variants yield low modelling errors and provide a suitable representation of the local flame state.
$\delta$-distribution for the flamelet index. The latter assumes that combustion occurs within a subfilter volume along one particular flamelet, the equivalence ratio of which is chosen dynamically. An a priori assessment of the proposed LES combustion model indicates a significant reduction of modelling error in comparison to models that do not account for thermodiffusive instabilities and an adequate subfilter closure. While a hydrogen-based progress variable formulation is found to perform slightly better in the a priori analysis than the water-based progress variable, both variants yield low modelling errors and provide a suitable representation of the local flame state.
In the second part, an a posteriori analysis of the newly proposed model is performed. For this, LES of the DNS configuration are performed, for which four different combustion models are tested: two model variants of the new LES combustion model that are based on mixture fraction and a hydrogen-based or water-based progress variable, a flamelet model that neglects differential diffusion effects, and an LES with a detailed chemical mechanism, which neglects any subfilter interactions. The flamelet model without differential diffusion effects significantly underpredicts the mean reaction rates within the flame front, yielding a significantly longer flame than the DNS. Further, it cannot reproduce the characteristic super-adiabatic temperatures, which are a clear marker of thermodiffusive instabilities. The LES with detailed chemical mechanism does not adequately represent the DNS yielding a too long flame and underpredicted super-adiabatic temperatures. The flamelet models with differential diffusion effects both perform well and approach the DNS closest. Among the two, the water-based progress variable formulation is found to perform slightly better if compared in terms of local flame state with the DNS data. The hydrogen-based progress variable leads to strong local overpredictions of the mixture fraction, yielding too high local super-adiabatic temperatures compared with the DNS. Thus, the combustion model based on a water-based progress variable and mixture fraction is recommended for future use. Remaining model deficiencies may be linked to the particular modelling of the subfilter scalar flux and the molecular diffusion terms, which require further investigation in future work. The former is modelled by a dynamic Smagorinsky model and further assessment of this term in thermodiffusively unstable turbulent flames is needed. For the latter, the subfilter correlation between the diffusion coefficients and the scalar gradients is neglected. Further validation of the presented models in other flame configurations will be also pursued in future work.
Acknowledgements
The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer Super-MUC at Leibniz Supercomputing Centre (LRZ, www.lrz.de).
Funding
Funding by the European Union (ERC Advanced Grant HYDROGENATE, 101054894) is gratefully acknowledged.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Mixture fraction transport equation for hydrogen-based progress variable
Using a water-based progress variable, Schlup & Blanquart (Reference Schlup and Blanquart2019) derived a mixture fraction transport equation for premixed hydrogen flames to account for the effects of differential diffusion. In the following, a transport equation of mixture fraction is derived if using a hydrogen-based progress variable. The derivation methodology is analogous to that of Schlup & Blanquart (Reference Schlup and Blanquart2019) and, hence, is kept brief.
Following Schlup & Blanquart (Reference Schlup and Blanquart2019), mixture fraction is defined as
where ![]() $Y_{F}$ and
$Y_{F}$ and ![]() $Y_{O}$ are the mass fractions of fuel and oxidizer;
$Y_{O}$ are the mass fractions of fuel and oxidizer; ![]() $Y_{F,1}$ and
$Y_{F,1}$ and ![]() $Y_{O,2}$ represent their values in the fuel and oxidizer stream, respectively. Here,
$Y_{O,2}$ represent their values in the fuel and oxidizer stream, respectively. Here, ![]() $\nu$ is the stoichiometric coefficient. Thus, the diffusion flux of mixture fraction
$\nu$ is the stoichiometric coefficient. Thus, the diffusion flux of mixture fraction ![]() $\boldsymbol {j}_{Z}$ is defined by the difference of the fuel and oxidizer diffusive fluxes,
$\boldsymbol {j}_{Z}$ is defined by the difference of the fuel and oxidizer diffusive fluxes, ![]() $\boldsymbol {j}_{F}$ and
$\boldsymbol {j}_{F}$ and ![]() $\boldsymbol {j}_{O}$:
$\boldsymbol {j}_{O}$:
Substituting the diffusive fluxes ![]() $\boldsymbol {j}_{F}$ and
$\boldsymbol {j}_{F}$ and ![]() $\boldsymbol {j}_{O}$ similar to Schlup & Blanquart (Reference Schlup and Blanquart2019) yields
$\boldsymbol {j}_{O}$ similar to Schlup & Blanquart (Reference Schlup and Blanquart2019) yields
 $$\begin{align} \boldsymbol{j}_{Z} &= \left(\frac{\rho}{\nu Y_{F,1} + Y_{O,2}} \right) {\cdot} \left[ -\nu \left(D_{F} \boldsymbol{\nabla} Y_{F} + D_{F}Y_{F} \frac{\boldsymbol{\nabla} W}{W} + \frac{D_{F}^{T}}{\rho} \frac{\boldsymbol{\nabla} T}{T} - Y_{F} \boldsymbol{u}^{C}\right) \right.\nonumber\\ &\quad \left.+ \left(D_{O} \boldsymbol{\nabla} Y_{O} + D_{O}Y_{O} \frac{\boldsymbol{\nabla} W}{W} + \frac{D_{O}^{T}}{\rho} \frac{\boldsymbol{\nabla} T}{T} - Y_{O} \boldsymbol{u}^{C}\right)\right] , \end{align}$$
$$\begin{align} \boldsymbol{j}_{Z} &= \left(\frac{\rho}{\nu Y_{F,1} + Y_{O,2}} \right) {\cdot} \left[ -\nu \left(D_{F} \boldsymbol{\nabla} Y_{F} + D_{F}Y_{F} \frac{\boldsymbol{\nabla} W}{W} + \frac{D_{F}^{T}}{\rho} \frac{\boldsymbol{\nabla} T}{T} - Y_{F} \boldsymbol{u}^{C}\right) \right.\nonumber\\ &\quad \left.+ \left(D_{O} \boldsymbol{\nabla} Y_{O} + D_{O}Y_{O} \frac{\boldsymbol{\nabla} W}{W} + \frac{D_{O}^{T}}{\rho} \frac{\boldsymbol{\nabla} T}{T} - Y_{O} \boldsymbol{u}^{C}\right)\right] , \end{align}$$
where ![]() $D_{F}$ and
$D_{F}$ and ![]() $D_{O}$ are the diffusion coefficients of fuel and oxidizer,
$D_{O}$ are the diffusion coefficients of fuel and oxidizer, ![]() $D_{F}^{T}$ and
$D_{F}^{T}$ and ![]() $D_{O}^{T}$ are the diffusion coefficients of fuel and oxidizer linked to the Soret effect,
$D_{O}^{T}$ are the diffusion coefficients of fuel and oxidizer linked to the Soret effect, ![]() $W$ is the mean molecular mass,
$W$ is the mean molecular mass, ![]() $\rho$ and
$\rho$ and ![]() $T$ are the density and temperature, and
$T$ are the density and temperature, and ![]() $\boldsymbol {u}^{C}$ is a correction velocity to ensure mass conservation, cf. Coffee & Heimerl (Reference Coffee and Heimerl1981). Assuming a one-step reaction, the following coupling function of fuel and oxidizer is obtained
$\boldsymbol {u}^{C}$ is a correction velocity to ensure mass conservation, cf. Coffee & Heimerl (Reference Coffee and Heimerl1981). Assuming a one-step reaction, the following coupling function of fuel and oxidizer is obtained
where the index ![]() $u$ indicates the unburned state. Rearrangement with the information that
$u$ indicates the unburned state. Rearrangement with the information that ![]() $Y_{F,u}=Y_{F,1} Z$ and
$Y_{F,u}=Y_{F,1} Z$ and ![]() $Y_{O,u}=Y_{O,2} (1-Z)$ yields
$Y_{O,u}=Y_{O,2} (1-Z)$ yields
Note that for a water-based progress variable, ![]() $Y_{O}$ needs to be expressed in terms of mixture fraction and the mass fraction of water, while a hydrogen-based progress variable requires
$Y_{O}$ needs to be expressed in terms of mixture fraction and the mass fraction of water, while a hydrogen-based progress variable requires ![]() $Y_{O}$ to be expressed in terms of mixture fraction and the mass fraction of hydrogen.
$Y_{O}$ to be expressed in terms of mixture fraction and the mass fraction of hydrogen.
When inserting (A5) into (A3) and neglecting the gradients of molar mass and correction velocity similar to Schlup & Blanquart (Reference Schlup and Blanquart2019), the diffusive fluxes of mixture fraction can be expressed as
 \begin{equation} \boldsymbol{j}_{Z} = \rho \nu \left( \frac{D_{H_2} - D_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) \boldsymbol{\nabla} Z + \rho D_{O_2} \boldsymbol{\nabla} Y_{H_2} + \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) \frac{\boldsymbol{\nabla} T}{T}. \end{equation}
\begin{equation} \boldsymbol{j}_{Z} = \rho \nu \left( \frac{D_{H_2} - D_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) \boldsymbol{\nabla} Z + \rho D_{O_2} \boldsymbol{\nabla} Y_{H_2} + \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) \frac{\boldsymbol{\nabla} T}{T}. \end{equation}
If defining the following diffusion coefficients ![]() ${D}_{Z}$ and
${D}_{Z}$ and ![]() ${D}^*_{Z}$,
${D}^*_{Z}$,
 $$\begin{gather}D_{Z}^T = \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) , \end{gather}$$
$$\begin{gather}D_{Z}^T = \left( \frac{\nu D^T_{H_2} - D^T_{O_2}}{ \nu Y_{H_2,F} + Y_{O_2,air} } \right) , \end{gather}$$the following transport of mixture fraction is obtained:
Note that this transport equation of mixture fraction is similar to that if using a water-based progress variable, cf. Schlup & Blanquart (Reference Schlup and Blanquart2019) or (2.4), but the expressions in (A7) and (A8) for the diffusion coefficients are different.
Appendix B. Maximum values of irreducible and modelling errors
To provide an additional quantitative assessment of irreducible and modelling errors, tables 4, 5 and 6 list the maximum error values of the conditional averages shown in figures 2, 12 and 13, respectively.
Table 4. List of maximum irreducible errors of the conditional averages shown in figure 2.

Table 5. Hydrogen-based progress variable: list of maximum modelling errors of the conditional averages shown in figure 12.

Table 6. Water-based progress variable: list of maximum modelling errors of the conditional averages shown in figure 13.














































































































