Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-11T10:33:31.647Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-Reynolds-number asymptotics of the streamwise normal stress in zero-pressure-gradient turbulent boundary layers

Published online by Cambridge University Press:  22 October 2015

Peter A. Monkewitz  and
Hassan M. Nagib
Peter A. Monkewitz*
Affiliation:
Faculty of Engineering Science, Ecole Polytechnique Fédérale de Lausanne (EPFL), CH-1015, Lausanne, Switzerland
Hassan M. Nagib
Affiliation:
MMAE Department, Illinois Institute of Technology, 10 W. 32nd St., E-1 Building, Chicago, IL 60616, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A more poetic long title could be ‘A voyage from the shifting grounds of existing data on zero-pressure-gradient (abbreviated ZPG) turbulent boundary layers (abbreviated TBLs) to infinite Reynolds number’. Aided by the requirement of consistency with the Reynolds-averaged momentum equation, the ‘shifting grounds’ are sufficiently consolidated to allow some firm conclusions on the asymptotic expansion of the streamwise normal stress 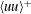$\langle uu\rangle ^{+}$, where the $^{+}$ indicates normalization with the friction velocity 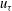$u_{{\it\tau}}$ squared. A detailed analysis of direct numerical simulation data very close to the wall reveals that its inner near-wall asymptotic expansion must be of the form 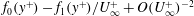$f_{0}(y^{+})-f_{1}(y^{+})/U_{\infty }^{+}+\mathit{O}(U_{\infty }^{+})^{-2}$, where 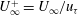$U_{\infty }^{+}=U_{\infty }/u_{{\it\tau}}$, 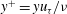$y^{+}=yu_{{\it\tau}}/{\it\nu}$ and 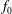$f_{0}$, 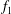$f_{1}$ are 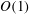$\mathit{O}(1)$ functions fitted to data in this paper. This means, in particular, that the inner peak of 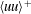$\langle uu\rangle ^{+}$ does not increase indefinitely as the logarithm of the Reynolds number but reaches a finite limit. The outer expansion of 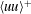$\langle uu\rangle ^{+}$, on the other hand, is constructed by fitting a large number of data from various sources. This exercise, aided by estimates of turbulence production and dissipation, reveals that the overlap region between inner and outer expansions of 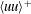$\langle uu\rangle ^{+}$ is its plateau or second maximum, extending to 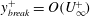$y_{\mathit{break}}^{+}=\mathit{O}(U_{\infty }^{+})$, where the outer logarithmic decrease towards the boundary layer edge starts. The common part of the two expansions of 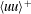$\langle uu\rangle ^{+}$, i.e. the height of the plateau or second maximum, is of the form 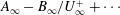$\,A_{\infty }-B_{\infty }/U_{\infty }^{+}+\cdots \,$with 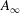$A_{\infty }$ and 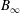$B_{\infty }$ constant. As a consequence, the logarithmic slope of the outer 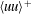$\langle uu\rangle ^{+}$ cannot be independent of the Reynolds number as suggested by ‘attached eddy’ models but must slowly decrease as 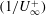$(1/U_{\infty }^{+})$. A speculative explanation is proposed for the puzzling finding that the overlap region of 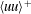$\langle uu\rangle ^{+}$ is centred near the lower edge of the mean velocity overlap, itself centred at 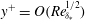$y^{+}=\mathit{O}(\mathit{Re}_{{\it\delta}_{\ast }}^{1/2})$ with 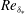$\mathit{Re}_{{\it\delta}_{\ast }}$ the Reynolds number based on free stream velocity and displacement thickness. Finally, similarities and differences between 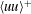$\langle uu\rangle ^{+}$ in ZPG TBLs and in pipe flow are briefly discussed.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 474 - 503
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
Banerjee, T. & Katul, G. G. 2013 Logarithmic scaling in the longitudinal velocity variance explained by a spectral budget. Phys. Fluids 25, 125106.CrossRefGoogle Scholar
Barenblatt, G. I. 1993 Scaling laws for fully developed turbulent shear flows. Part I. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.CrossRefGoogle Scholar
Barenblatt, G. I., Chorin, A. J., Hald, O. H. & Prostokishin, V. M. 1997 Structure of the zero-pressure-gradient turbulent boundary layer. Proc. Natl Acad. Sci. USA 29, 7817–7819.CrossRefGoogle Scholar
Bradshaw, P. 1967 The turbulence structure of equilibrium boundary layers. J. Fluid Mech. 29, 625–645.CrossRefGoogle Scholar
Bruns, J. M., Fernholz, H.-H. & Monkewitz, P. A. 1993 An experimental investigation of a three-dimensional turbulent boundary layer in an ‘S’-shaped duct. J. Fluid Mech. 393, 175–213.CrossRefGoogle Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Chauhan, K., Philip, J., DeSilva, Ch. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Cimarelli, A., De Angelis, E., Schlatter, P., Brethouwer, G., Talamelli, A. & Casciola, C. M. 2015 Sources and fluxes of scale energy in the overlap layer of wall turbulence. J. Fluid Mech. 771, 407–423.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Mech. 4, 1–51.Google Scholar
Coles, D. E. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244.Google Scholar
Crighton, D. G. & Leppington, F. G. 1973 Singular perturbation methods in acoustics: diffraction by a plate of finite thickness. Proc. R. Soc. Lond. A 335, 313–339.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds-number scaling of the flat-plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.CrossRefGoogle Scholar
Eitel-Amor, G., Örlü, R. & Schlatter, P. 2014 Simulation and validation of a spatially evolving turbulent boundary layer up to $\text{Re}_{{\it\theta}}=8300$ . Intl J. Heat Fluid Flow 47, 57–69.CrossRefGoogle Scholar
Fernholz, H. H., Janke, G., Schober, M., Wagner, P. M. & Warnack, D. 1996 New developments and applications of skin-friction measuring techniques. Meas. Sci. Technol. 7, 1396–1409.CrossRefGoogle Scholar
George, W. K. 2006 Recent advancements toward the understanding of turbulent boundary layers. AIAA 44, 2435–2449.CrossRefGoogle Scholar
George, W. K. & Castillo, L. 1997 Zero-pressure-gradient turbulent boundary layer. Appl. Mech. Rev. 50, 689–729.CrossRefGoogle Scholar
Hites, M. H.1997 Scaling of high-Reynolds number turbulent boundary layers in the National Diagnostic Facility. PhD thesis, Illinois Institute of Technology, USA.Google Scholar
Hultmark, M. 2012 A theory for the streamwise turbulent fluctuations in high Reynolds number pipe flow. J. Fluid Mech. 707, 575–584.CrossRefGoogle Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501, 1–5.CrossRefGoogle ScholarPubMed
Hutchins, N., Chauhan, K., Marusic, I., Monty, J. P. & Klewicki, J. 2012 Towards reconciling the large-scale structure of turbulent boundary layers in the atmosphere and laboratory. Boundary-Layer Meteorol. 145, 273–306.CrossRefGoogle Scholar
Jimenez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.CrossRefGoogle Scholar
Kevorkian, J. & Cole, J. D. 1985 Perturbation Methods in Applied Mathematics. Springer.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Klewicki, J. C. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.CrossRefGoogle Scholar
Klewicki, J. C., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365, 823–839.Google ScholarPubMed
Knobloch, K. & Fernholz, H.-H. 2004 Statistics, correlations and scaling in a turbulent boundary layer at $Re\leqslant 1.15\times 10^{5}$ . In Proc. of IUTAM Symp. on Reynolds Number Scaling in Turbulent Flow in Fluid Mechanics and its Applications (ed. Smits, A. J.), vol. 74, pp. 11–16. Springer.Google Scholar
Kulandaivelu, Vigneshwaran2011 Evolution and structure of zero pressure gradient turbulent boundary layer. PhD thesis, University of Melbourne.Google Scholar
Laadhari, F. 2007 Reynolds number effect on the dissipation function in wall-bounded flows. Phys. Fluids 19, 038101.CrossRefGoogle Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103, 1–24.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3 (11 pp.).CrossRefGoogle Scholar
Marusic, I. & Perry, A. E. 1995 A wall wake model for the turbulent structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Mellor, G. L. 1972 The large Reynolds number, asymptotic theory of turbulent boundary layers. Intl J. Engng Sci. 10, 851–873.CrossRefGoogle Scholar
Metzger, M., McKeon, B. J. & Holmes, H. 2007 The near-neutral atmospheric surface layer: turbulence and non-stationarity. Phil. Trans. R. Soc. Lond. A 365 (1852), 859–876.Google ScholarPubMed
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.CrossRefGoogle Scholar
Millikan, C. M. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of 5th International Congress in Applied Mechanics. Wiley.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2007 Self-consistent high-Reynolds-number asymptotics for zero-pressure-gradient turbulent boundary layers. Phys. Fluids 19, 115101.CrossRefGoogle Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20, 105102.CrossRefGoogle Scholar
Monkewitz, P. A., Duncan, R. D. & Nagib, H. M. 2010 Correcting hot-wire measurements of stream-wise turbulence intensity in boundary layers. Phys. Fluids 22, 091701.CrossRefGoogle Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.CrossRefGoogle Scholar
Nagib, H. M., Chauhan, K. A. & Monkewitz, P. A.2005 Scaling of high Reynolds number turbulent boundary layers revisited. In 4th AIAA Theoretical Fluid Mechanics Meeting, Toronto, Canada. AIAA 2005–4810.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. M., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. A 365, 807–822.Google ScholarPubMed
Österlund, J. M.1999 Experimental studies of zero pressure-gradient turbulent boundary layer flow. PhD thesis, Kungl Tekniska Högskolan, Royal Institute of Technology, Sweden.Google Scholar
Panton, R. L. 2009 Scaling and correlation of vorticity fluctuations in turbulent channels. Phys. Fluids 21, 115104, 1–11.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. M. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Prandtl, L. 1925 Über die ausgebildete Turbulenz. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Rotta, J. C. 1962 Turbulent boundary layers in incompressible flow. Prog. Aeronaut. Sci. 2, 1–219.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
Simens, M. P., Jimenez, J., Hoyas, S. & Mizuno, Y. 2009 A high-resolution code for turbulent boundary layers. J. Comput. Phys. 228, 4218–4231.CrossRefGoogle Scholar
Spalart, P. R. 1988 Direct simulation of turbulent boundary layer up to $R_{{\it\theta}}=1410$ . J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
Tsuji, Y. 1999 Peak position of dissipation spectrum in turbulent boundary layers. Phys. Rev. E 59, 7235–7238.CrossRefGoogle ScholarPubMed
Vallikivi, M.2014 Wall-bounded turbulence at high Reynolds numbers. PhD thesis, Princeton University, USA.Google Scholar
Wark, C. E.1988 Experimental investigation of coherent structures in turbulent boundary layers. PhD thesis, Illinois Institute of Technology, USA.Google Scholar