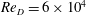Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T07:10:15.290Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-eddy simulation of flow over a rotating cylinder: the lift crisis at $Re_{D}=6\times 10^{4}$

Published online by Cambridge University Press:  19 September 2018

W. Cheng Open the ORCID record for W. Cheng [Opens in a new window] ,
D. I. Pullin  and
R. Samtaney
W. Cheng*
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 23955-6900 Graduate Aerospace Laboratories, California Institute of Technology, CA91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, CA91125, USA
R. Samtaney
Affiliation:
Mechanical Engineering, Physical Science and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 23955-6900
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present wall-resolved large-eddy simulation (LES) of flow with free-stream velocity 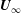$\boldsymbol{U}_{\infty }$ over a cylinder of diameter 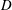$D$ rotating at constant angular velocity 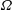$\unicode[STIX]{x1D6FA}$, with the focus on the lift crisis, which takes place at relatively high Reynolds number 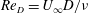$Re_{D}=U_{\infty }D/\unicode[STIX]{x1D708}$, where $\unicode[STIX]{x1D708}$ is the kinematic viscosity of the fluid. Two sets of LES are performed within the (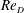$Re_{D}$, $\unicode[STIX]{x1D6FC}$)-plane with 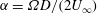$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FA}D/(2U_{\infty })$ the dimensionless cylinder rotation speed. One set, at 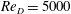$Re_{D}=5000$, is used as a reference flow and does not exhibit a lift crisis. Our main LES varies $\unicode[STIX]{x1D6FC}$ in 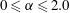$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 2.0$ at fixed 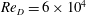$Re_{D}=6\times 10^{4}$. For $\unicode[STIX]{x1D6FC}$ in the range 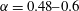$\unicode[STIX]{x1D6FC}=0.48{-}0.6$ we find a lift crisis. This range is in agreement with experiment although the LES shows a deeper local minimum in the lift coefficient than the measured value. Diagnostics that include instantaneous surface portraits of the surface skin-friction vector field 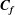$\boldsymbol{C}_{\boldsymbol{f}}$, spanwise-averaged flow-streamline plots, and a statistical analysis of local, near-surface flow reversal show that, on the leeward-bottom cylinder surface, the flow experiences large-scale reorganization as $\unicode[STIX]{x1D6FC}$ increases through the lift crisis. At 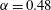$\unicode[STIX]{x1D6FC}=0.48$ the primary-flow features comprise a shear layer separating from that side of the cylinder that moves with the free stream and a pattern of oscillatory but largely attached flow zones surrounded by scattered patches of local flow separation/reattachment on the lee and underside of the cylinder surface. Large-scale, unsteady vortex shedding is observed. At 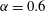$\unicode[STIX]{x1D6FC}=0.6$ the flow has transitioned to a more ordered state where the small-scale separation/reattachment cells concentrate into a relatively narrow zone with largely attached flow elsewhere. This induces a low-pressure region which produces a sudden decrease in lift and hence the lift crisis. Through this process, the boundary layer does not show classical turbulence behaviour. As $\unicode[STIX]{x1D6FC}$ is further increased at constant 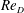$Re_{D}$, the localized separation zone dissipates with corresponding attached flow on most of the cylinder surface. The lift coefficient then resumes its increasing trend. A logarithmic region is found within the boundary layer at 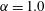$\unicode[STIX]{x1D6FC}=1.0$.

JFM classification

Boundary Layers: Boundary layer separation Boundary Layers: Boundary Layers Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 371 - 407
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achenbach, E. 1968 Distribution of local pressure and skin friction around a circular cylinder in cross-flow up to Re = 5 × 106 . J. Fluid Mech. 34, 625–639.Google Scholar
Aldoss, T. K. & Abou-Arab, T. W. 1990 Experimental study of the flow around a rotating cylinder in crossflow. Exp. Therm. Fluid Sci. 3 (3), 316–322.Google Scholar
Aljure, D. E., Rodríguez, I., Lehmkuhl, O., Pérez-Segarra, C. D. & Oliva, A. 2015 Influence of rotation on the flow over a cylinder at Re = 5000. Intl J. Heat Fluid Flow 55, 76–90.Google Scholar
Carstensen, S., Mandviwalla, X., Vita, L. & Paulsen, U. S. 2014 Lift of a rotating circular cylinder in unsteady flows. J. Ocean Wind Energy 1, 41–49.Google Scholar
Cheng, W., Pullin, D. I. & Samtaney, R. 2018 Large-eddy simulation of flow over a grooved cylinder up to transcritical Reynolds numbers. J. Fluid Mech. 835, 327–362.Google Scholar
Cheng, W., Pullin, D. I., Samtaney, R., Zhang, W. & Gao, W. 2017 Large-eddy simulation of flow over a cylinder with Re D from 3. 9 × 103 to 8. 5 × 105 : a skin-friction perspective. J. Fluid Mech. 820, 121–158.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Chung, D. & Pullin, D. I. 2009 Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 631, 281–309.Google Scholar
Dryden, H. L., Murnaghan, F. D. & Bateman, H.1932 Report of the Committee on Hydrodynamics. Tech. Rep. 84. National Research Council.Google Scholar
Fletcher, C. A. J. 1972 Negative Magnus forces in the critical Reynolds number regime. J. Aircraft 9 (12), 826–834.Google Scholar
Kim, J., Choi, H., Park, H. & Yoo, J. Y. 2014 Inverse Magnus effect on a rotating sphere: when and why. J. Fluid Mech. 754, R2.Google Scholar
Lehmkuhl, O., Rodríguez, I., Borrell, R., Chiva, J. & Oliva, A. 2014 Unsteady forces on a circular cylinder at critical Reynolds numbers. Phys. Fluids 26 (12), 125110.Google Scholar
Lundgren, T. S. 1982 Strained spiral vortex model for turbulent fine structure. Phys. Fluids 25 (12), 2193–2203.Google Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9 (8), 2443–2454.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.Google Scholar
Peller, H. 1986 Thermofluiddynamic experiments with a heated and rotating circular cylinder in crossflow. II – Boundary layer profiles and location of separation points. Exp. Fluids 4, 223–231.Google Scholar
Reid, E. G.1924 Tests of rotating cylinders. Tech. Rep. 209. National Advisory Committee for Aeronautics.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10 (03), 345–356.Google Scholar
Schewe, G. 1983 On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers. J. Fluid Mech. 133, 265–285.Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21, 205–234.Google Scholar
Son, J. S. & Hanratty, T. J. 1969 Velocity gradients at the wall for flow around a cylinder at Reynolds numbers from 5 × 103 to 105 . J. Fluid Mech. 35 (2), 353–368.Google Scholar
Swanson, W. M. 1961 The Magnus effect: A summary of investigations to date. Trans. ASME: J. Basic Engng 83 (3), 461–470.Google Scholar
Takayama, S. & Aoki, K. 2005 Flow characteristics around a rotating grooved circular cylinder with grooved of different depths. J. Vis. 8 (4), 295–303.Google Scholar
Thom, A.1931 Experiments on the flow past a rotating cylinder. Tech. Rep. 1410. Reports and Memoranda.Google Scholar
Thom, A.1934 Effect of discs on the air forces on a rotating cylinder. Tech. Rep. 1623. Reports and Memoranda.Google Scholar
Voelkl, T., Pullin, D. I. & Chan, D. C. 2000 A physical-space version of the stretched-vortex subgrid-stress model for large-eddy simulation. Phys. Fluids 12, 1810–1825.Google Scholar
Zhang, W., Cheng, W., Gao, W., Qamar, A. & Samtaney, R. 2015 Geometrical effects on the airfoil flow separation and transition. Comput. Fluids 116, 60–73.Google Scholar
Zhang, W. & Samtaney, R. 2016 Low-Re flow past an isolated cylinder with rounded corners. Comput. Fluids 136, 384–401.Google Scholar