Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-03T15:59:15.440Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-amplitude topographic waves in 2D stratified flow

Published online by Cambridge University Press:  16 June 2011

DAVID J. MURAKI
DAVID J. MURAKI*
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Our fundamental understanding of steady, stratified flow over two-dimensional (2D) topography rests on the pioneering works of G. Lyra and R. Long. Within linear theory, Lyra established the far-field radiation conditions that determine the downstream pattern of buoyancy waves. Soon after, Long discovered that the steady, nonlinear streamfunction for special cases of stratified, 2D flow could satisfy the same equations as linear theory, subject to an exact topographic boundary condition. Fourier methods are currently used to compute solutions to Long's theory for arbitrary topography in the near-hydrostatic or small-amplitude topographic parameter regimes. It is not generally appreciated however, that these methods encounter difficulties for flows that are both strongly non-hydrostatic and beyond linear amplitudes. By recasting Long's theory into a linear integral equation, this difficulty is shown to be a computational barrier associated with an ill-conditioning of the Fourier method. The problem is overcome through the development of a boundary integral computation which relies on some lesser known solutions from Lyra's original analysis. This method is well-conditioned for strongly non-hydrostatic flows, and is used to extend the exploration of critical overturning flows over Gaussian and bell-shaped ridges. These results indicate that the critical value of the non-dimensional height (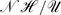) asymptotes to a finite value with increasing non-hydrostatic parameter ().

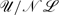JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 681 , 25 August 2011 , pp. 173 - 192
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. National Bureau of Standards.Google Scholar
Aguilar, D. A., Sutherland, B. R. & Muraki, D. J. 2006 Laboratory generation of internal waves from sinusoidal topography. Deep-Sea Res. II 53, 96–115.Google Scholar
Alexander, D. E. 2004 Stability of Steady, Stratified Flow over Two-Dimensional Topography. Masters thesis. Simon Fraser University.Google Scholar
Brown, D. J. & Christie, D. R. 1998 Fully nonlinear solitary waves in continuously stratified incompressible Boussinesq fluids. Phys. Fluids 10, 2569–2586.Google Scholar
Chandler-Wilde, S. N., Ross, C. R. & Zhang, B. 1999 Scattering by infinite one-dimensional rough surfaces. Proc. R. Soc. A 455, 3767–3787.Google Scholar
Drazin, P. G. & Su, C. H. 1975 A note on long-wave theory of airflow over a mountain. J. Atmos. Sci. 32, 437–439.Google Scholar
Dubreil-Jacotin, M.-L. 1932 Sur les ondes de type permanent dans les liquides hétérogènes. Atti della R. Acc. Naz. dei Lincei 15, 814–819.Google Scholar
Dubreil-Jacotin, M.-L. 1935 Complément à une note antérieure sur les ondes de type permanent dans les liquides hétérogènes. Atti della R. Acc. Naz. dei Lincei 21, 344–346.Google Scholar
Dubreil-Jacotin, M.-L. 1937 Sur les théoremes d'existence relatifs aux ondes permanentes périodiques à deux dimensions dans les liquides hétérogènes. J. Math. Pures Appl. 16, 43–67.Google Scholar
Durran, D. R. 1992 Two-layer solutions to Long's equation for vertically propagating mountain waves: How good is linear theory? Quart. J. Roy. Meteor. Soc. 118, 415–433.Google Scholar
Green, C. D. 1969 Integral Equation Methods. Barnes & Noble.Google Scholar
Grubisić, V. & Lewis, J. M. 2004 Sierra wave project revisited. BAMS 8, 1127–1142.Google Scholar
Kantzios, Y. D. & Akylas, T. R. 1993 An asymptotic theory of nonlinear stratified flow of large depth over topography. Proc. R. Soc. Lond. A 440, 639–653.Google Scholar
Kondo, J. 1991 Integral Equations. Oxford University Press.Google Scholar
Kozhevnikov, V. N. 1968 Orographic perturbations in the two-dimensional stationary problem. Atmos. Ocean. Phys. (Izv. Akad. nauk SSSR, Fiz. atmos. okeana) 4, 16–27.Google Scholar
Laprise, R. & Peltier, W. R. 1989 On the structural characteristics of steady finite-amplitude mountain waves over bell-shaped topography. J. Atmos. Sci. 46 (4), 1498–1529.Google Scholar
Lilly, D. K. & Klemp, J. B. 1979 The effects of terrain shape on nonlinear hydrostatic mountain waves. J. Fluid. Mech. 95 (2), 241–261.Google Scholar
Llewellen-Smith, S. G. & Young, W. R. 2003 Tidal conversion at a very steep ridge. J. Fluid Mech. 495, 175–191.CrossRefGoogle Scholar
Long, R. R. 1953 Some aspects of the flow of stratifed fluids. i. A theoretical investigation. Tellus 5 (1), 42–58.CrossRefGoogle Scholar
Long, R. R. 1955 Some aspects of the flow of stratifed fluids. iii. Continuous density gradients. Tellus 7 (3), 341–357.Google Scholar
Lyra, G. 1940 Über den Einfluß von Bodenerhebungen auf die Strömung einer stabil geschichteten Atmosphäre. Beitr. Phys. Freien Atmos. 26, 197–206.Google Scholar
Lyra, G. 1943 Theorie der stationären Leewellenströmung in freier Atmosphäre. Z. Angew. Math. Mech. 28, 1–28.Google Scholar
Miles, J. W. 1968 Lee waves in a stratified flow. Part 2. Semi-circular obstacle. J. Fluid Mech. 33 (4), 803–814.Google Scholar
Miles, J. W. & Huppert, H. E. 1969 Lee waves in a stratified flow. Part 4. Perturbation approximations. J. Fluid Mech. 35 (3), 497–525.Google Scholar
Queney, P. 1948 The problem of air flow over mountains: A summary of theoretical results. Bull. Am. Meteor. Soc. 29, 16–26.CrossRefGoogle Scholar
Queney, P., Corby, G. A., Gerbier, N., Koschmieder, H. & Zierep, J. 1960 The airflow over mountains. Tech. Rep. 34. World Meteorological Organization, Geneva, Switzerland.Google Scholar
Raymond, D. J. 1972 Calculation of airflow over an arbitrary ridge including diabatic heating and cooling. J. Atmos. Sci. 29, 837–843.Google Scholar
Robinson, R. M. 1969 The effects of a barrier on internal waves. Deep-Sea Res. 16, 421–429.Google Scholar
Scorer, R. S. 1949 Theory of waves in the lee of mountains. Q. J. R. Meteorol. Soc. 75, 41–56.Google Scholar
Smith, R. B. 1977 The steepening of hydrostatic mountain waves. J. Atmos. Sci. 34, 1634–1654.Google Scholar
Smith, R. B. 1979 The influence of mountains on the atmosphere. In Advances in Geophysics, vol. 21, pp. 87–230. Elsevier.Google Scholar
Smith, R. B. 1980 Linear theory of stratified hydrostatic flow past an isolated mountain. Tellus, vol. 32, pp. 348–364.CrossRefGoogle Scholar
Trefethen, L. N. & Bau, D. 1997 Numerical Linear Algebra. SIAM.Google Scholar
Wing, G. M. 1991 A Primer on Integral Equations of the First Kind. SIAM.Google Scholar
Wuertle, M. G., Sharman, R. D. & Datta, A. 1996 Atmospheric lee waves. Annu. Rev. Fluid Mech. 28, 429–476.Google Scholar
Yih, C.-S. 1960 Exact solutions for steady two-dimensional flow of a stratified fluid. J. Fluid Mech. 9, 161–174.CrossRefGoogle Scholar