Published online by Cambridge University Press: 21 May 2018
The spatial signature of spanwise velocity coherence in turbulent boundary layers has been studied using a series of unique large-field-of-view multicamera particle image velocimetry experiments, which were configured to capture streamwise/spanwise slices of the boundary layer in both the logarithmic and the wake regions. The friction Reynolds number of 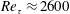 $Re_{\unicode[STIX]{x1D70F}}\approx 2600$ was chosen to nominally match the simulation of Sillero et al. (Phys. Fluids, vol. 26 (10), 2014, 105109), who had previously reported oblique features of the spanwise coherence at the top edge of the boundary layer based on the sign of the spanwise velocity, and here we find consistent observations from experiments. In this work, we show that these oblique features in the spanwise coherence relate to the intermittent turbulent bulges at the edge of the layer, and thus the geometry of the turbulent/non-turbulent interface, with the clear appearance of two counter-oriented oblique features. Further, these features are shown to be also present in the logarithmic region once the velocity fields are deconstructed based on the sign of both the spanwise and the streamwise velocity, suggesting that the often-reported meandering of the streamwise-velocity coherence in the logarithmic region is associated with a more obvious diagonal pattern in the spanwise velocity coherence. Moreover, even though a purely visual inspection of the obliqueness in the spanwise coherence may suggest that it extends over a very large spatial extent (beyond many boundary layer thicknesses), through a conditional analysis, we show that this coherence is limited to distances nominally less than two boundary layer thicknesses. Interpretation of these findings is aided by employing synthetic velocity fields of a boundary layer constructed using the attached eddy model, where the range of eddy sizes can be prescribed. Comparisons between the model, which employs an array of self-similar packet-like eddies that are randomly distributed over the plane of the wall, and the experimental velocity fields reveal a good degree of agreement, with both exhibiting oblique features in the spanwise coherence over comparable spatial extents. These findings suggest that the oblique features in the spanwise coherence are likely to be associated with similar structures to those used in the model, providing one possible underpinning structural composition that leads to this behaviour. Further, these features appear to be limited in spatial extent to only the order of the large-scale motions in the flow.
$Re_{\unicode[STIX]{x1D70F}}\approx 2600$ was chosen to nominally match the simulation of Sillero et al. (Phys. Fluids, vol. 26 (10), 2014, 105109), who had previously reported oblique features of the spanwise coherence at the top edge of the boundary layer based on the sign of the spanwise velocity, and here we find consistent observations from experiments. In this work, we show that these oblique features in the spanwise coherence relate to the intermittent turbulent bulges at the edge of the layer, and thus the geometry of the turbulent/non-turbulent interface, with the clear appearance of two counter-oriented oblique features. Further, these features are shown to be also present in the logarithmic region once the velocity fields are deconstructed based on the sign of both the spanwise and the streamwise velocity, suggesting that the often-reported meandering of the streamwise-velocity coherence in the logarithmic region is associated with a more obvious diagonal pattern in the spanwise velocity coherence. Moreover, even though a purely visual inspection of the obliqueness in the spanwise coherence may suggest that it extends over a very large spatial extent (beyond many boundary layer thicknesses), through a conditional analysis, we show that this coherence is limited to distances nominally less than two boundary layer thicknesses. Interpretation of these findings is aided by employing synthetic velocity fields of a boundary layer constructed using the attached eddy model, where the range of eddy sizes can be prescribed. Comparisons between the model, which employs an array of self-similar packet-like eddies that are randomly distributed over the plane of the wall, and the experimental velocity fields reveal a good degree of agreement, with both exhibiting oblique features in the spanwise coherence over comparable spatial extents. These findings suggest that the oblique features in the spanwise coherence are likely to be associated with similar structures to those used in the model, providing one possible underpinning structural composition that leads to this behaviour. Further, these features appear to be limited in spatial extent to only the order of the large-scale motions in the flow.