Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T14:37:14.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Laminar spread of a circular liquid jet impinging axially on a rotating disc

Published online by Cambridge University Press:  07 February 2019

B. Scheichl Open the ORCID record for B. Scheichl [Opens in a new window]  and
A. Kluwick
B. Scheichl*
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Faculty of Mechanical Engineering, Technische Universität Wien, Tower BA/E322, Getreidemarkt 9, 1060 Vienna, Austria AC2T research GmbH (Austrian Excellence Center for Tribology), Viktor-Kaplan-Straße 2/C, 2700 Wiener Neustadt, Austria
A. Kluwick
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, Faculty of Mechanical Engineering, Technische Universität Wien, Tower BA/E322, Getreidemarkt 9, 1060 Vienna, Austria
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The steady laminar annular spread of a thin liquid film generated by a circular jet which impinges perpendicularly in direction of gravity on the centre of a rotating disc is examined both analytically and numerically. Matched asymptotic expansions of the flow quantities provide the proper means for studying the individual flow regimes arising due to the largeness of the Reynolds number formed with the radius of the jet, its slenderness and the relative magnitude of the centrifugal body force. This is measured by a suitably defined Rossby number, 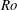$Ro$. The careful analysis of jet impingement predicts a marked influence of gravity and surface tension on the film flow, considered in the spirit of a shallow-water approach, only through the vorticity imposed by the jet flow. Accordingly, associated downstream conditions are disregarded as the local Froude and Weber numbers are taken to be sufficiently large. Hence, the parabolic problem shaped from the governing equations in a rigorous manner describes the strongly supercritical spread of a developed viscous film past an infinite disc, essentially controlled by 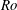$Ro$. Its numerical solutions are discussed for a wide range of values of 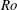$Ro$. The different flow regimes reflecting varying effects of viscous shear and centrifugal force are elucidated systematically to clarify the surprising richness of flow phenomena. Special attention is paid to the cases 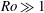$Ro\gg 1$ and 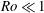$Ro\ll 1$. The latter, referring to relatively high disc spin, implies a delicate breakdown of the asymptotic flow structure, thus requiring a specific analytical and numerical treatment. Finally, the impact of gravity and capillarity and thus of the disc edge on the film flow is envisaged in brief.

JFM classification

Geophysical and Geological Flows: Rotating flows Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 449 - 489
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aroesty, J., Gross, J. F., Illickal, M. M. & Maloney, J. V. 1967 Blood oxygenation: a study in bioengineering mass transfer. In Digest Seventh International Conference on Medical and Biological Engineering, Stockholm, p. 527 (also: RAND Corporation, Rep. P-8732, 1967).Google Scholar
Astarita, T. & Cardone, G. 2008 Convective heat transfer on a rotating disk with a centred impinging round jet. Intl J. Heat Mass Transfer 51 (7–8), 1562–1572.Google Scholar
Basu, S. & Cetegen, B. M. 2006a Analysis of hydrodynamics and heat transfer in a thin liquid film flow flowing over a rotating disk by the integral method. Trans. ASME J. Heat Transfer 128 (3), 217–225.Google Scholar
Basu, S. & Cetegen, B. M. 2006b Effect of hydraulic jump on hydrodynamics and heat transfer in a thin liquid film flowing over a rotating disk analyzed by integral method. Trans. ASME J. Heat Transfer 129 (5), 657–663.Google Scholar
Batchelor, G. K. 1970 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bhagat, R. K., Jha, N. K., Linden, P. F. & Wilson, D. I. 2018 On the origin of the circular hydraulic jump in a thin liquid film. J. Fluid Mech. 851, R5-1–R5-11.Google Scholar
Birkhoff, G. & Zarantonello, E. H. 1957 Jets, Wakes, and Cavities, Applied Mathematics and Mechanics, vol. 2. Academic.Google Scholar
Bowles, R. I. & Smith, F. T. 1992 The standing hydraulic jump: theory, computations and comparisons with experiments. J. Fluid Mech. 242, 145–168.Google Scholar
Bradbury, L. J. S. 1972 The impact of an axisymmetric jet onto a normal ground. Aeronaut. Q. 23 (2), 141–147.Google Scholar
Brauer, H. 1971 Grundlagen der Einphasen- und Mehrphasenströmungen (in German). Sauerländer.Google Scholar
Broderson, S., Metzger, D. E. & Fernando, H. J. S. 1996a Flows generated by the impingement of a jet on a rotating surface: part I – basic flow patterns. Trans. ASME J. Fluids Engng 118 (1), 61–67.Google Scholar
Broderson, S., Metzger, D. E. & Fernando, H. J. S. 1996b Flows generated by the impingement of a jet on a rotating surface: part II – detailed flow structure and analysis. Trans. ASME J. Fluids Engng 118 (1), 68–73.Google Scholar
Brotherton-Ratcliffe, R. V. & Smith, F. T. 1989 Viscous effects can destabilize linear and nonlinear water waves. Theor. Comput. Fluid Dyn. 1 (1), 21–39.Google Scholar
Charwat, A. F., Kelly, R. E. & Gazley, C. 1972 The flow and stability of thin liquid films on a rotating disk. J. Fluid Mech. 53 (2), 227–255.Google Scholar
Cholemari, M. R. & Arakeri, J. H. 2005 Waves on radial film flows. Phys. Fluids 17 (8), 084108.Google Scholar
Cochran, W. G. 1934 The flow due to a rotating disc. Proc. Camb. Phil. Soc. 30 (3), 365–375.Google Scholar
Chandrasakhar, S. 1981 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Deshpande, M. D. D. & Vaishnav, R. N. Submerged laminar jet impingement on a plane. J. Fluid Mech. 114, 213–236.Google Scholar
Dorfman, L. A. 1965 Calculation of the boundary layer on an arbitrary axisymmetric surface rotating in a still medium. J. Appl. Mech. Tech. Phys. 6 (3), 62–65.Google Scholar
Dorfman, L. A. 1967 Flow and heat transfer in a viscous layer on a spinning disc. J. Engng Phys. 12 (3), 309–316.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids, Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press.Google Scholar
Gurevich, M. I. 1961 Influence of capillary forces upon the coefficient of contraction of a jet. J. Appl. Math. Mech. 25 (6), 1586–1596; original Russian article in Prikl. Math. Mech. 25 (6) 1961, 1060–1067.Google Scholar
Gurevich, M. I. 1966 The Theory of Jets in an Ideal Fluid, Int’l Series of Monographs in Pure and Applied Mathematics, vol. 39. Pergamon Press.Google Scholar
Hannah, D. M.1947 Forced flow against a rotating disc. Rep. Memor. aero. Res. Coun., Lond. No. 2772.Google Scholar
Higuera, F. J. 1993 Natural convection below a downward facing horizontal plate. Eur. J. Mech. (B/Fluids) 12 (3), 289–311.Google Scholar
Higuera, F. J. 1994 The hydraulic jump in a viscous laminar flow. J. Fluid Mech. 274, 69–92.Google Scholar
Higuera, F. J. 1997 The circular hydraulic jump. Phys. Fluids 9 (5), 1476–1478; Brief communications.Google Scholar
Higuera, F. J. & Liñán, A. 1993 Choking conditions for nonuniform viscous flow. Phys. Fluids A 5 (3), 568–570; Brief communications.Google Scholar
Homann, F. 1936 Der Einfluß großer Zähigkeit bei der Strömung um den Zylinder und um die Kugel. Z. Angew. Math. Mech. 16, 153–164; (in German). Engl. transl.: The effect of high viscosity on the flow around a cylinder and around a sphere. Tech. Memor. nat. adv. Comm. Aero., Wash. No. 1334.Google Scholar
von Kármán, Th. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. (ZAMM) 1, 233–252; (in German). Engl. transl.: On laminar and turbulent friction. NACA Tech. Mem. 1092.Google Scholar
Khayat, R. E. 2016 Slipping free jet flow near channel exit at moderate Reynolds number for large slip length. J. Fluid Mech. 793, 667–708.Google Scholar
Khayat, R. E. 2017 Initial development of a free-surface wall jet at moderate Reynolds number. J. Fluid Mech. 826, 235–269.Google Scholar
Kim, T. S. & Kim, M. U. 2009 The flow and hydrodynamic stability of a liquid film on a rotating disc. Fluid Dyn. Res. 41 (3), 035504.Google Scholar
Lagrée, P.-Y. 1999 Thermal mixed convection induced locally by a step change in surface temperature in a Poiseuille flow in the framework of triple deck theory. Intl J. Heat Mass Transfer 42 (14), 2509–2524.Google Scholar
Lienhard V, J. H. 1995 Liquid jet impingement. In Ann. Rev. Heat Transfer (ed. Tien, C.-L.), vol. VI, chap. 4, pp. 199–270. Begell House.Google Scholar
Liu, X., Gabour, L. A. & Lienhard V, J. H. 1993 Stagnation-point heat transfer during impingement of laminar liquid jets: analysis including surface tension. Trans. ASME J. Heat Transfer 115 (1), 99–105.Google Scholar
Liu, X. & Lienhard, J. H. 1993 The hydraulic jump in circular jet impingement and in other thin liquid films. Exp. Fluids 15 (2), 108–116.Google Scholar
McCarthy, M. J. & Molloy, N. A. 1974 Review of stability of liquid jets and the influence of nozzle design. Chem. Engng J. 7 (1), 1–20.Google Scholar
Mohajer, B. & Li, R. 2015 Circular hydraulic jump on finite surfaces with capillary limit. Phys. Fluids 27 (11), 117102.Google Scholar
Needham, D. J. & Merkin, J. H. 1987 The development of nonlinear waves on the surface of a horizontally rotating thin liquid film. J. Fluid Mech. 184, 357–379.Google Scholar
Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow, Series in Computational Methods in Mechanics and Thermal Sciences. CRC Press.Google Scholar
Phares, D. J., Smedley, G. T. & Flagan, R. C. 2000a The inviscid impingement of a jet with arbitrary velocity profile. Phys. Fluids 12 (8), 2046–2055.Google Scholar
Phares, D. J., Smedley, G. T. & Flagan, R. C. 2000b The wall shear stress produced by the normal impingement of jet on a flat surface. J. Fluid Mech. 418, 351–375.Google Scholar
Prieling, D. & Steiner, H. 2013a Analysis of the wall mass transfer on spinning disks using an integral boundary layer method. Chem. Engng Sci. 101, 109–119.Google Scholar
Prieling, D. & Steiner, H. 2013b Unsteady thin film flow on spinning disks at large Ekman numbers using an integral boundary layer method. Intl J. Heat Mass Transfer 65, 10–22.Google Scholar
Prieling, D., Steiner, H. & Brenn, G. 2012a Integral analysis of the flow dynamics and mass transfer in a wavy liquid film on a spinning disk. Proc. Appl. Maths Mech. 12 (1), 521–522.Google Scholar
Prieling, D., Steiner, H. & Brenn, G. 2012b Numerical analysis of hydrodynamic characteristics of wavy liquid films on rotating disks. In Proceedings of European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, September 10–14, 2012, pp. 15. Technische Universität Wien.Google Scholar
Prosirov, A. É. & Riabchuk, G. V. 1995 Viscous incompressible flow over the surface of a rotary disk. Fluid Dyn. 30 (6), 833–837; original Russian article in Izv. Ross. Akad. Nauk, Mekh. Zhidk. Gaza 6, 1995, 39–43.Google Scholar
Rahman, M. M. & Faghri, A. 1992 Numerical simulation of fluid flow and heat transfer in a liquid film over a rotating disk. Intl J. Heat Mass Transfer 35 (6), 1441–1453.Google Scholar
Rauscher, J. W., Kelly, R. E. & Cole, J. D. 1973 An asymptotic solution for the laminar flow of a thin film on a rotating disk. Trans. ASME J. Appl. Mech. 40, 43–47.Google Scholar
Rosenhead, L.(Ed.) 1963 Laminar Boundary Layers, The Fluid Motion Memoirs. Oxford University Press.Google Scholar
Rubel, A. 1980 Computations of jet impingement on a flat surface. AIAA J. 18 (2), 168–175.Google Scholar
Rubel, A. 1983 Inviscid axisymmetric jet impingement with recirculating stagnation regions. AIAA J. 21 (3), 351–357.Google Scholar
Scheichl, B., Bowles, R. I. & Pasias, G. 2018 Developed liquid film passing a trailing edge under the action of gravity and capillarity. J. Fluid Mech. 850, 924–953.Google Scholar
Schlichting, H. & Gersten, K. 2017 Boundary-Layer Theory, 9th edn. Springer; with contributions from E. Krause and H. Oertel Jr.Google Scholar
Shevchuk, I. V. 2009 Convective Heat and Mass Transfer in Rotating Disk Systems. Springer.Google Scholar
Sisoev, G. M., Matar, O. K. & Lawrence, C. J. 2003 Axisymmetric wave regimes in viscous liquid film flow over a spinning disk. J. Fluid Mech. 495, 385–411.Google Scholar
Steinrück, H. 1994 Mixed convection over a cooled horizontal plate: non-uniqueness and numerical instabilities of the boundary-layer equations. J. Fluid Mech. 278, 251–265.Google Scholar
Thomas, S., Faghri, A. & Hankey, W. 1991 Experimental analysis and flow visualization of a thin liquid film on a stationary and rotating disk. Trans. ASME J. Fluids Engng 113 (1), 73–80.Google Scholar
Tifford, A. N. & Chu, S. T. 1952 On the flow around a rotating disk in a uniform stream. J. Aeronaut. Sci. 19 (4), 284–285.Google Scholar
Tillett, J. P. K. 1968 On the laminar flow in a free jet of liquid at high Reynolds numbers. J. Fluid Mech. 32 (2), 273–292.Google Scholar
Trefftz, E. 1916 Über die Kontraktion kreisförmiger Flüssigkeitsstrahlen. Z. Math. Phys. 64 (1), 34–61; (in German).Google Scholar
Vita, P., Gschaider, B. W. F., Prieling, D. & Steiner, H. 2012 Thin film flow simulation on a rotating disc. In Proc. European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012), Vienna, Austria, September 10–14, 2012, p. 11 pp.Google Scholar
Wang, Y. & Khayat, R. E. 2018 Impinging jet flow and hydraulic jump on a rotating disk. J. Fluid. Mech. 839, 525–560.Google Scholar
Watson, E. J. 1964 The radial spread of a liquid jet over a horizontal plane. J. Fluid Mech. 20 (3), 481–499.Google Scholar
Webb, B. W. & Ma, C.-F. 1995 Single-phase liquid jet impingement heat transfer. In Adv. Heat Transf. (ed. Sparrow, E. M., Abraham, J. P. & Gorham, J. M.), vol. 26, pp. 105–217. Elsevier.Google Scholar
Zandbergen, P. J. & Dijkstra, D. 1987 Von Kármán swirling flows. Annu. Rev. Fluid Mech. 19, 465–491.Google Scholar