Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T23:26:20.421Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian transport properties of pulmonary interfacial flows

Published online by Cambridge University Press:  09 November 2011

Bradford J. Smith ,
Sarah Lukens ,
Eiichiro Yamaguchi  and
Donald P. Gaver III
Bradford J. Smith
Affiliation:
Department of Biomedical Engineering, Tulane University, New Orleans, LA 70118, USA
Sarah Lukens
Affiliation:
Mathematics Department, Tulane University, New Orleans, LA 70118, USA Department of Mathematics, University of Pittsburgh, Pittsburgh, PA 15260, USA
Eiichiro Yamaguchi
Affiliation:
Department of Biomedical Engineering, Tulane University, New Orleans, LA 70118, USA
Donald P. Gaver III*
Affiliation:
Department of Biomedical Engineering, Tulane University, New Orleans, LA 70118, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Disease states characterized by airway fluid occlusion and pulmonary surfactant insufficiency, such as respiratory distress syndrome, have a high mortality rate. Understanding the mechanics of airway reopening, particularly involving surfactant transport, may provide an avenue to increase patient survival via optimized mechanical ventilation waveforms. We model the occluded airway as a liquid-filled rigid tube with the fluid phase displaced by a finger of air that propagates with both mean and sinusoidal velocity components. Finite-time Lyapunov exponent (FTLE) fields are employed to analyse the convective transport characteristics, taking note of Lagrangian coherent structures (LCSs) and their effects on transport. The Lagrangian perspective of these techniques reveals flow characteristics that are not readily apparent by observing Eulerian measures. These analysis techniques are applied to surfactant-free velocity fields determined computationally, with the boundary element method, and measured experimentally with micro particle image velocimetry (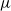-PIV). We find that the LCS divides the fluid into two regimes, one advected upstream (into the thin residual film) and the other downstream ahead of the advancing bubble. At higher oscillatory frequencies particles originating immediately inside the LCS experience long residence times at the air–liquid interface, which may be conducive to surfactant transport. At high frequencies a well-mixed attractor region is identified; this volume of fluid cyclically travels along the interface and into the bulk fluid. The Lagrangian analysis is applied to velocity data measured with 0.01 mg ml−1 of the clinical pulmonary surfactant Infasurf in the bulk fluid, demonstrating flow field modifications with respect to the surfactant-free system that were not visible in the Eulerian frame.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Biological Fluid Dynamics: Pulmonary fluid mechanics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 234 - 257
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Adrian, R. J. 1991 Particle-imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23, 261–304.CrossRefGoogle Scholar
2. Adrian, R. J. 2005 Twenty years of particle image velocimetry. Exp. Fluids 39, 159–169.CrossRefGoogle Scholar
3. Bilek, A. M., Dee, K. C. & Gaver, D. P. III 2003 Mechanisms of surface-tension-induced epithelial cell damage in a model of pulmonary airway reopening. J. Appl. Physiol. 94, 770–783.Google Scholar
4. Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.CrossRefGoogle Scholar
5. Drescher, K., Leptos, K. C., Tuval, I., Ishikawa, T., Pedley, T. J. & Goldstein, R. E. 2009 Dancing Volvox: hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102 (16).CrossRefGoogle ScholarPubMed
6. Gaver, D. P. III, Halpern, D., Jensen, O. E. & Grotberg, J. B. 1996 The steady motion of a semi-infinite bubble through a flexible-walled channel. J. Fluid Mech. 319, 25–65.CrossRefGoogle Scholar
7. Gaver, D. P. III, Samsel, R. W. & Solway, J. 1990 Effects of surface tension and viscosity on airway reopening. J. Appl. Physiol. 69, 74–85.CrossRefGoogle ScholarPubMed
8. Ghadiali, S. N. & Gaver, D. P. III 2000 An investigation of pulmonary surfactant physicochemical behaviour under airway reopening conditions. J. Appl. Physiol. 88, 493–506.CrossRefGoogle ScholarPubMed
9. Ghadiali, S. N. & Gaver, D. P. III 2003 The influence of non-equilibrium surfactant dynamics on the flow of a semi-infinite bubble in a rigid cylindrical capillary tube. J. Fluid Mech. 478, 165–196.CrossRefGoogle Scholar
10. Ghadiali, S. N., Halpern, D. & Gaver, D. P. III 2001 A dual-reciprocity boundary element method for evaluating bulk convective transport of surfactant in free-surface flows. J. Comput. Phys. 171, 534–559.CrossRefGoogle Scholar
11. Glindmeyer, W. IV, Smith, B. & Gaver, D. 2011 In situ enhancement of pulmonary surfactant function using temporary flow reversal. J. Appl. Physiol. (in press).CrossRefGoogle Scholar
12. Grotberg, J. B. 2001 Respiratory fluid mechanics and transport processes. Annu. Rev. Biomed. Engng 3, 421–457.CrossRefGoogle ScholarPubMed
13. Haber, S., Butler, J., Brenner, H., Emanuel, I. & Tsuda, A. 2000 Shear flow over a self-similar expanding pulmonary alveolus during rhythmical breathing. J. Fluid Mech. 405, 243–268.CrossRefGoogle Scholar
14. Haller, G. 1999 Finding finite time invariant manifolds in two-dimensional velocity fields. Chaos 10 (1), 99–108.CrossRefGoogle Scholar
15. Haller, G. 2001a Distinguished material surfaces and coherent structures in three-dimensional fluid flows. Physica D 149, 248–277.CrossRefGoogle Scholar
16. Haller, G. 2001b Lagrangian coherent structures and the rate of strain in two-dimensional turbulence. Phys. Fluids A 13, 3365–3385.CrossRefGoogle Scholar
17. Haller, G. 2002 Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14 (6), 1851–1861.CrossRefGoogle Scholar
18. Haller, G. & Poje, A. C. 1998 Finite time transport in aperiodic flows. Physica D 119, 352–380.CrossRefGoogle Scholar
19. Halpern, D. & Gaver, D. P. III 1994 Boundary element analysis of the time-dependent motion of a semi-infinite bubble in a channel. J. Comput. Phys. 115, 366–375.CrossRefGoogle Scholar
20. Halpern, D., Naire, S., Jensen, O. E. & Gaver, D. P. III 2005 Unsteady bubble propagation in a flexible channel: predictions of a viscous stick-slip instability. J. Fluid Mech. 528, 53–86.CrossRefGoogle Scholar
21. Heil, M. 2001 Finite Reynolds number effects in the Bretherton problem. Phys. Fluids 13, 2517–2521.CrossRefGoogle Scholar
22. Jensen, O. E., Horsburgh, M. K., Halpern, D. & Gaver, D. P. 2002 The steady propagation of a bubble in a flexible-walled channel: asymptotic and computational models. Phys. Fluids 14 (2), 443–457.CrossRefGoogle Scholar
23. Kay, S. S., Bilek, A. M., Dee, K. C. & Gaver, D. P. III 2004 Pressure gradient, not exposure duration, determines the extent of epithelial cell damage in a model of pulmonary airway reopening. J. Appl. Physiol. 97, 269–276.CrossRefGoogle ScholarPubMed
24. Launois-Surpas, M. A., Ivanova, T., Panaiotov, I., Proust, J. E., Puisieux, F. & Georgiev, G. 1992 Behavior of pure and mixed DPPC liposomes spread or adsorbed at the air–water interface. Colloid Polym. Sci. 270 (9), 901–911.Google Scholar
25. Lewis, D. M. & Pedley, T. J. 2000 Planktonic contact rates in homogeneous isotropic turbulence: theoretical predictions and kinematic simulations. J. Theor. Biol. 205 (3), 377–408.CrossRefGoogle ScholarPubMed
26. Lu, W.-Q. & Chang, H.-C. 1988 An extension of the biharmonic boundary integral method to free surface flow in channels. J. Comput. Phys. 77, 340–360.CrossRefGoogle Scholar
27. Mancho, A. M. & Wiggins, S. 2006 A tutorial on dynamical systems concepts applied to Lagrangian transport in oceanic flows defined as finite time data sets: theoretical and computational issues. Phys. Rep. 437, 55–124.CrossRefGoogle Scholar
28. Matthay, M. A., Bhattacharya, S., Gaver, D. P. III, Ware, L. B., Lim, L. H. K., Syrkina, O., Eyal, F. & Hubmayr, R. 2002 Ventilator-induced lung injury: in vivo and in vitro mechanisms. Am. J. Physiol. Lung Cell Mol. Physiol. 283, L678–L682.CrossRefGoogle ScholarPubMed
29. Naire, S. & Jensen, O. E. 2005 Epithelial cell deformation during surfactant-mediated airway reopening: a theoretical model. J. Appl. Physiol. 99 (2), 458–471.Google Scholar
30. Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge University Press.Google Scholar
31. Park, C. M. & Homsy, G. W. 1984 Two-phase displacement in Hele-Shaw cells: theory. J. Fluid Mech. 139, 291–308.CrossRefGoogle Scholar
32. Pedley, T. J. 1980 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.CrossRefGoogle Scholar
33. Pedley, T. J. & Kamm, R. D. 1988 The effect of secondary motion on axial transport in oscillatory tube flow. J. Fluid Mech. 193, 347–367.CrossRefGoogle Scholar
34. Pillert, J. E. & Gaver, D. P. III 2009 Physicochemical effects enhance surfactant transport in pulsatile motion of a semi-infinite bubble. Biophys. J. 96, 312–327.Google Scholar
35. Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flows. Cambridge University Press.CrossRefGoogle Scholar
36. Reinelt, D. A. & Saffman, P. G. 1985 The penetration of a finger into a viscous fluid in a channel and tube. SIAM J. Sci. Stat. Comput. 6 (3), 542.CrossRefGoogle Scholar
37. Reinsch, C. 1967 Smoothing by spline functions. Numer. Math. 10, 177–183.CrossRefGoogle Scholar
38. Rubenfeld, G. D., Caldwell, E., Peabody, E., Weaver, J., Martin, D. P., Neff, M., Stern, E. J. & Hudson, L. D. 2005 Incidence and outcomes of acute lung injury. N. Engl. J. Med. 353, 1685–1693.CrossRefGoogle ScholarPubMed
39. Santiago, J. G., Wereley, S. T., Meinhart, C. D., Beebe, D. J. & Adrian, R. J. 1998 A particle image velocimetry system for microfluidics. Exp. Fluids 25, 316–319.CrossRefGoogle Scholar
40. Shadden, S. C. & Taylor, C. A. 2008 Characterization of coherent structures in the cardiovascular system. Ann. Biomed. Engng 36 (7), 1152–1162.CrossRefGoogle ScholarPubMed
41. Shadden, S. C., Dabiri, J. O. & Marsden, J. E. 2006 Lagrangian analysis of fluid transport in empirical vortex ring flows. Phys. Fluids 18, 047105.CrossRefGoogle Scholar
42. Shadden, S. C., Lekien, F. & Marsden, J. 2005 Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Physica D 212, 271–304.CrossRefGoogle Scholar
43. Shen, E. I. & Udell, K. S. 1985 A finite element study of low Reynolds number two-phase flow in cylindrical tubes. Trans. ASME: J. Appl. Mech. 52, 253–256.CrossRefGoogle Scholar
44. Smith, B. J. & Gaver, D. P. III 2008 The pulsatile propagation of a finger of air within a fluid-occluded cylindrical tube. J. Fluid Mech. 601, 1–23.CrossRefGoogle ScholarPubMed
45. Smith, B. J., Yamaguchi, E. & Gaver, D. P. III 2010 A translating stage system for -PIV measurements surrounding the tip of a migrating semi-infinite bubble. Meas. Sci. Technol. 21 (1), 015401.CrossRefGoogle Scholar
46. Stebe, K. J. & Barthes-Biesel, D. 1995 Marangoni effects of adsorption–desorption controlled surfactants on the leading edge of an infinitely long bubble in a capillary. J. Fluid Mech. 286, 25–48.Google Scholar
47. Yamaguchi, E., Smith, B. J. & Gaver, D. P. III 2009 Micro-PIV measurements of the flow field surrounding a migrating semi-infinite bubble. Exp. Fluids 47 (2), 309–320.Google Scholar
48. Yap, D. Y. K. & Gaver, D. P. III 1998 The influence of surfactant on two-phase flow in a flexible-walled channel under bulk equilibrium conditions. Phys. Fluids 10 (8), 1846–1863.CrossRefGoogle Scholar
49. Zambon, M. & Vincent, J.-L. 2008 Mortality rates for patients with acute lung injury/ARDS have decreased over time. Chest 133, 1120–1127.CrossRefGoogle ScholarPubMed
50. Zimmer, M. E., Williams, H. A. R. & Gaver, D. P. III 2005 The pulsatile motion of a semi-infinite bubble in a channel: flow fields, and transport of an inactive surface-associated contaminant. J. Fluid Mech. 537, 1–33.CrossRefGoogle Scholar