Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T18:38:30.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian transport in a class of three-dimensional buoyancy-driven flows

Published online by Cambridge University Press:  26 October 2017

P. S. Contreras ,
M. F. M. Speetjens Open the ORCID record for M. F. M. Speetjens [Opens in a new window]  and
H. J. H. Clercx
P. S. Contreras
Affiliation:
Energy Technology Laboratory, Department of Mechanical Engineering, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands Fluid Dynamics Laboratory, Department of Applied Physics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
M. F. M. Speetjens*
Affiliation:
Energy Technology Laboratory, Department of Mechanical Engineering, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
H. J. H. Clercx
Affiliation:
Fluid Dynamics Laboratory, Department of Applied Physics, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present study concerns the Lagrangian dynamics of three-dimensional (3D) buoyancy-driven cavity flows under steady and laminar conditions due to a global temperature gradient imposed via an opposite hot and cold sidewall. This serves as the archetypal configuration for natural-convection flows in which (contrary to the well-known Rayleigh–Bénard flow) gravity is perpendicular (instead of parallel) to the global temperature gradient. Limited insight into the Lagrangian properties of this class of flows, despite its relevance to observed flow phenomena as well as scalar transport, motivates this study. The 3D Lagrangian dynamics are investigated in terms of the generic structure and associated transport properties of the global streamline pattern (‘Lagrangian flow topology’) by both theoretical and computational analyses. The Grashof number 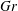$Gr$ is the principal control parameter for the flow topology: limit 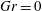$Gr=0$ yields a trivial state of closed streamlines; 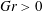$Gr>0$ induces symmetry breaking by fluid inertia and buoyancy and thus causes formation of toroidal coherent structures (‘primary tori’) embedded in chaotic streamlines governed by Hamiltonian mechanisms. Fluid inertia prevails for ‘smaller’ 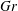$Gr$ and gives behaviour that is dynamically entirely analogous to 3D lid-driven cavity flows. Buoyancy-induced bifurcation of the flow topology occurs for ‘larger’ 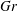$Gr$ and underlies the emergence of ‘secondary rolls’ observed in the literature and to date unreported secondary tori for ‘larger’ Prandtl numbers 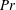$Pr$. Key to these dynamics are stagnation points and corresponding heteroclinic manifold interactions.

JFM classification

Mixing: Chaotic advection Convection: Convection in cavities Mathematical Foundations: Topological fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , pp. 5 - 40
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aref, H. 2002 The development of chaotic advection. Phys. Fluids 14 (4), 1315–1325.Google Scholar
Aref, H., Blake, J. R., Budišić, M., Cardoso, S. S. S., Cartwright, J. H. E., Clercx, H. J. H., Feudel, U., Golestanian, R., Gouillart, E., Le Guer, Y. et al. 2017 Frontiers of chaotic advection. Rev. Mod. Phys. 89, 025007.CrossRefGoogle Scholar
Arfken, G. B. & Weber, H. J. 2005 Mathematical Methods for Physicists. Elsevier.Google Scholar
Arnol’d, V. I. 1989 Mathematical Methods of Classical Mechanics. Springer.CrossRefGoogle Scholar
Awbi, H. B. 2008 Ventilation Systems: Design and Performance. Taylor & Francis.Google Scholar
Bajer, K. 1994 Hamiltonian formulation of the equations of streamlines in three-dimensional steady flows. Chaos Solitons Fractals 4 (6), 895–911.Google Scholar
Batchelor, G. K. 1954 Heat transfer by free convection across a closed cavity between vertical boundaries at different temperatures. Q. Appl. Maths 12 (3), 209–233.CrossRefGoogle Scholar
Bejan, A. 2013 Convection Heat Transfer. Wiley.CrossRefGoogle Scholar
Bennett, B., Anne, V. & Hsueh, J. 2006 Natural convection in a cubic cavity: implicit numerical solution of two benchmark problems. Numer. Heat Transfer A 50 (2), 99–123.CrossRefGoogle Scholar
Bird, R. B., Stewart, W. E. & Lightfoot, E. N. 2007 Transport Phenomena. Wiley.Google Scholar
Borjini, M. N., Aissia, H. B., Halouani, K. & Zeghmati, B. 2008 Effect of radiative heat transfer on the three-dimensional buoyancy flow in cubic enclosure heated from the side. Intl J. Heat Fluid Flow 29 (1), 107–118.CrossRefGoogle Scholar
Brouwer, L. E. J. 1911 Über Abbildung von Mannigfaltigkeiten. Math. Ann. 71, 97–115.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Cartwright, J. H. E., Feingold, M. & Piro, O. 1996 Chaotic advection in three-dimensional unsteady incompressible laminar flow. J. Fluid Mech. 316, 259–284.CrossRefGoogle Scholar
Cheng, C. Q. & Sun, Y. S. 1990a Existence of invariant tori in three-dimensional measure preserving mappings. Celest. Mech. 47, 275–292.Google Scholar
Cheng, C. Q. & Sun, Y. S. 1990b Existence of periodically invariant curves in three-dimensional measure-preserving mappings. Celest. Mech. 47, 293–303.CrossRefGoogle Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765–777.CrossRefGoogle Scholar
Contreras, P. S., de la Cruz, L. M. & Ramos, E. 2016a Topological analysis of a mixing flow generated by natural convection. Phys. Fluids 28 (1), 013602.CrossRefGoogle Scholar
Contreras, P. S., Speetjens, M. F. M. & Clercx, H. J. H. 2016b Buoyancy-induced Lagrangian chaos: the differentially-heated cavity revisited. J. Phys. Conf. Ser. 745 (3), 032039.CrossRefGoogle Scholar
Davies, G. F. 2011 Mantle Convection for Geologists. Cambridge University Press.CrossRefGoogle Scholar
Elder, J. W. 1965 Laminar free convection in a vertical slot. J. Fluid Mech. 23 (1), 77–98.CrossRefGoogle Scholar
Franjione, J. G. & Ottino, J. M. 1992 Symmetry concepts for the geometric analysis of mixing flows. Proc. R. Soc. Lond. A 338 (1650), 301–323.Google Scholar
Getling, A. V. 1998 Rayleigh–Bénard Convection: Structures and Dynamics. World Scientific.CrossRefGoogle Scholar
Giaiotti, D. B., Steinacker, R. & Stel, F. 2007 Atmospheric Convection: Research and Operational Forecasting Aspects. Springer.CrossRefGoogle Scholar
Gill, A. E. 1966 The boundary-layer regime for convection in a rectangular cavity. J. Fluid Mech. 26 (3), 515–536.CrossRefGoogle Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer.CrossRefGoogle Scholar
Henkes, R. A. W. M. & Hoogendoorn, C. J. 1990 On the stability of the natural convection flow in a square cavity heated from the side. Appl. Sci. Res. 47 (3), 195–220.CrossRefGoogle Scholar
Henle, M. 1979 A Combinatorial Introduction to Topology. Freeman.Google Scholar
Henry, D. & Benhadid, H. 2007 Multiple flow transitions in a box heated from the side in low-Prandtl-number fluids. Phys. Rev. E 76, 016314.Google Scholar
Henry, D. & Buffat, M. 1998 Two-and three-dimensional numerical simulations of the transition to oscillatory convection in low-Prandtl-number fluids. J. Fluid Mech. 374, 145–171.CrossRefGoogle Scholar
Henry, D., Juel, A., Ben Hadid, H. & Kaddeche, S. 2008 Directional effect of a magnetic field on oscillatory low-Prandtl-number convection. Phys. Fluids 20 (3), 034104.CrossRefGoogle Scholar
Hiller, W. J., Koch, St. & Kowalewski, T. A. 1989 Three-dimensional structures in laminar natural convection in a cubic enclosure. Exp. Therm. Fluid Sci. 2 (1), 34–44.CrossRefGoogle Scholar
Hiller, W. J., Koch, St., Kowalewski, T. A., de Vahl Davis, G. & Behnia, M. 1990 Experimental and numerical investigation of natural convection in a cube with two heated side walls. In Proceedings of IUTAM Symposium, Cambridge, UK August 13-18, 1989 (ed. Moffatt, K. & Tsinober, A.), pp. 717–726. Cambridge University Press.Google Scholar
Hof, B., Juel, A. & Mullin, T. 2005 Magnetohydrodynamic damping of oscillations in low-Prandtl-number convection. J. Fluid Mech. 545, 193–201.CrossRefGoogle Scholar
Hof, B., Juel, A., Zhao, L., Henry, D., Ben Hadid, H. & Mullin, T. 2004 On the onset of oscillatory convection in molten gallium. J. Fluid Mech. 515, 391–413.CrossRefGoogle Scholar
Ishii, K., Ota, C. & Adachi, S. 2012 Streamlines near a closed curve and chaotic streamlines in steady cavity flows. Procedia IUTAM 5, 173–186.CrossRefGoogle Scholar
Juel, A., Mullin, T., Ben Hadid, H. & Henry, D. 1999 Magnetohydrodynamic convection in molten gallium. J. Fluid Mech. 378, 97–118.CrossRefGoogle Scholar
Juel, A., Mullin, T., Ben Hadid, H. & Henry, D. 2001 Three-dimensional free convection in molten gallium. J. Fluid Mech. 436, 267–281.CrossRefGoogle Scholar
Kelmanson, M. A. & Lonsdale, B. 1996 Eddy genesis in the double-lid-driven cavity. Q. J. Mech. Appl. Maths 49 (4), 635–655.CrossRefGoogle Scholar
Kowalewski, T. A. 1998 Experimental validation of numerical codes in thermally driven flows. In In Adv. Comput. Heat Transfer, pp. 1–15. Begel House Inc.Google Scholar
Labrosse, G., Tric, E., Khallouf, H. & Betrouni, M. 1997 A direct (pseudo-spectral) solver of the 2D/3D Stokes problem: Transition to unsteadiness of natural-convection flow in a differentially heated cubical cavity. Numer. Heat Transfer B 31 (3), 261–276.CrossRefGoogle Scholar
Lappa, M. 2010 Thermal Convection: Patterns, Evolution and Stability. Wiley.Google Scholar
Laure, P. 1987 Study on convective motions in a rectangular cavity with a horizontal gradient of temperature. J. Méc. Théor. Appl. 6 (3), 351–382.Google Scholar
MacKay, R. S., Meiss, J. D. & Percival, I. C. 1984 Stochasticity and transport in hamiltonian systems. Phys. Rev. Lett. 52, 697.CrossRefGoogle Scholar
Mallinson, G. D. & de Vahl Davis, G. 1973 The method of the false transient for the solution of coupled elliptic equations. J. Comput. Phys. 12 (4), 435–461.CrossRefGoogle Scholar
Mallinson, G. D. & de Vahl Davis, G. 1977 Three-dimensional natural convection in a box: a numerical study. J. Fluid Mech. 83 (01), 1–31.Google Scholar
Markatos, N. C. & Pericleous, K. A. 1984 Laminar and turbulent natural convection in an enclosed cavity. Intl J. Heat Mass Transfer 27 (5), 755–772.CrossRefGoogle Scholar
McKell, K. E., Broomhead, D. S., Jones, R. & Hurle, D. T. J. 1990 Torus doubling in convecting molten gallium. Europhys. Lett. 12 (6), 513.CrossRefGoogle Scholar
Meiss, J. D. 2015 Thirty years of turnstiles and transport. Chaos 25 (9), 097602.CrossRefGoogle ScholarPubMed
Melnikov, D. E. & Shevtsova, V. M. 2005 Liquid particles tracing in three-dimensional buoyancy-driven flows. Fluid Dyn. Mater. Process. 1, 189–199.Google Scholar
Mercader, I., Batiste, O., Ramírez-Piscina, L., Ruiz, X., Rüdiger, S. & Casademunt, J. 2005 Bifurcations and chaos in single-roll natural convection with low Prandtl number. Phys. Fluids 17 (10), 104108.CrossRefGoogle Scholar
Metcalfe, G., Speetjens, M. F. M., Lester, D. R. & Clercx, H. J. H. 2012 Beyond passive: Chaotic transport in stirred fluids. In Advances in Applied Mechanics (ed. van der Giessen, E. & Aref, H.), vol. 45, pp. 109–188. Elsevier.Google Scholar
Moharana, N. R., Speetjens, M. F. M., Trieling, R. R. & Clercx, H. J. H. 2013 Three-dimensional Lagrangian transport phenomena in unsteady laminar flows driven by a rotating sphere. Phys. Fluids 25 (9), 093602.CrossRefGoogle Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media. Springer.Google Scholar
Ostrach, S. 1972 Natural convection in enclosures. Adv. Heat Transfer 8, 161–227.Google Scholar
Ostrach, S. 1988 Natural convection in enclosures. Trans. ASME J. Heat Transfer 110, 1175–1190.CrossRefGoogle Scholar
Oteski, L., Duguet, Y. & Pastur, L. R. 2014 Lagrangian chaos in confined two-dimensional oscillatory convection. J. Fluid Mech. 759, 489–519.Google Scholar
Oteski, L., Duguet, Y., Pastur, L. R. & Le Quéré, P. 2015 Quasiperiodic routes to chaos in confined two-dimensional differential convection. Phys. Rev. E 92 (4), 043020.Google ScholarPubMed
Ott, E. 2002 Chaos in Dynamical Systems. Cambridge University Press.CrossRefGoogle Scholar
Pallares, J., Arroyo, M. P., Grau, F. X. & Giralt, F. 2001 Experimental laminar Rayleigh–Bénard convection in a cubical cavity at moderate Rayleigh and Prandtl numbers. Exp. Fluids 31 (2), 208–218.Google Scholar
Phillips, T. N. 1984 Natural convection in an enclosed cavity. J. Comput. Phys. 54 (3), 365–381.CrossRefGoogle Scholar
Sankar, M., Bhuvaneswari, M., Sivasankaran, S. & Do, Y. 2011 Buoyancy induced convection in a porous cavity with partially thermally active sidewalls. Intl J. Heat Mass Transfer 54 (25), 5173–5182.CrossRefGoogle Scholar
Sezai, I. & Mohamad, A. A. 1999 Three-dimensional double-diffusive convection in a porous cubic enclosure due to opposing gradients of temperature and concentration. J. Fluid Mech. 400, 333–353.Google Scholar
Shankar, P. N. 1997 Three-dimensional eddy structure in a cylindrical container. J. Fluid Mech. 342, 97–118.CrossRefGoogle Scholar
Shankar, P. N. 1998 Three-dimensional Stokes flow in a cylindrical container. Phys. Fluids 10 (3), 540–549.CrossRefGoogle Scholar
Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136.CrossRefGoogle Scholar
Shankar, P. N., Meleshko, V. V. & Nikiforovich, E. I. 2002 Slow mixed convection in rectangular containers. J. Fluid Mech. 471, 203–217.CrossRefGoogle Scholar
Sheu, T. W. H., Rani, H. P., Tan, T.-C. & Tsai, S. F. 2008 Multiple states, topology and bifurcations of natural convection in a cubical cavity. Comput. Fluids 37 (8), 1011–1028.CrossRefGoogle Scholar
Soucasse, L., Rivière, P., Soufiani, A., Xin, S. & Le Quéré, P. 2014 Transitional regimes of natural convection in a differentially heated cubical cavity under the effects of wall and molecular gas radiation. Phys. Fluids 26 (2), 024105.CrossRefGoogle Scholar
Speetjens, M. F. M. & Clercx, H. J. H. 2005 A spectral solver for the Navier–Stokes equations in the velocity–vorticity formulation. Intl J. Comput. Fluid Dyn. 19 (3), 191–209.CrossRefGoogle Scholar
Speetjens, M. F. M. & Clercx, H. J. H. 2013 Formation of coherent structures in a class of realistic 3D unsteady flows. In Fluid Dynamics in Physics, Engineering and Environmental Applications (ed. Klapp, J. et al. ), pp. 139–157. Springer.CrossRefGoogle Scholar
Speetjens, M. F. M., Clercx, H. J. H. & van Heijst, G. J. F. 2004 A numerical and experimental study on advection in three-dimensional Stokes flows. J. Fluid Mech. 514, 77–105.CrossRefGoogle Scholar
Speetjens, M. F. M., Clercx, H. J. H. & van Heijst, G. J. F. 2006 Merger of coherent structures in time-periodic viscous flows. Chaos 16 (4), 043104,1–8.CrossRefGoogle ScholarPubMed
Speetjens, M. F. M., Demissie, E. A., Metcalfe, G. & Clercx, H. J. H. 2014 Lagrangian transport characteristics of a class of three-dimensional inline-mixing flows with fluid inertia. Phys. Fluids 26, 113601.CrossRefGoogle Scholar
Torres, J. F., Henry, D., Komiya, A. & Maruyama, S. 2014 Bifurcation analysis of steady natural convection in a tilted cubical cavity with adiabatic sidewalls. J. Fluid Mech. 756, 650–688.Google Scholar
Torres, J. F., Henry, D., Komiya, A. & Maruyama, S. 2015 Transition from multiplicity to singularity of steady natural convection in a tilted cubical enclosure. Phys. Rev. E 92 (2), 023031.Google Scholar
Turcotte, D. L. & Schubert, G. 2002 Geodynamics. Cambridge University Press.CrossRefGoogle Scholar
de Vahl Davis, G. 1968 Laminar natural convection in an enclosed rectangular cavity. Intl J. Heat Mass Transfer 11 (11), 1675–1693.CrossRefGoogle Scholar
de Vahl Davis, G. 1983 Natural convection of air in a square cavity: a bench mark numerical solution. Intl J. Numer. Meth. Fluids 3 (3), 249–264.CrossRefGoogle Scholar
Wakashima, S. & Saitoh, T. S. 2004 Benchmark solutions for natural convection in a cubic cavity using the high-order time–space method. Intl J. Heat Mass Transfer 47 (4), 853–864.CrossRefGoogle Scholar
Wu, F., Speetjens, M. F. M., Vainchtein, D. L., Trieling, R. R. & Clercx, H. J. H. 2014 Comparative numerical-experimental analysis of the universal impact of arbitrary perturbations on transport in three-dimensional unsteady flows. Phys. Rev. E 90 (6), 063002.Google ScholarPubMed
Yarin, A. L., Kowalewski, T. A., Hiller, W. J. & Koch, St. 1996 Distribution of particles suspended in convective flow in differentially heated cavity. Phys. Fluids 8 (5), 1130–1140.CrossRefGoogle Scholar
Znaien, J., Speetjens, M. F. M., Trieling, R. R. & Clercx, H. J. H. 2012 Observability of periodic lines in three-dimensional lid-driven cylindrical cavity flows. Phys. Rev. E 85 (6), 066320.Google Scholar