Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-20T19:40:28.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Laboratory study of the breaking and energy distribution of internal solitary waves over a ridge

Published online by Cambridge University Press:  02 December 2024

Yulin Guo Open the ORCID record for Yulin Guo [Opens in a new window] ,
Xu Chen Open the ORCID record for Xu Chen [Opens in a new window] ,
Qun Li Open the ORCID record for Qun Li [Opens in a new window]  and
Jing Meng Open the ORCID record for Jing Meng [Opens in a new window]
Yulin Guo
Affiliation:
Key Laboratory of Physical Oceanography, Ocean University of China and Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, PR China
Xu Chen*
Affiliation:
Key Laboratory of Physical Oceanography, Ocean University of China and Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, PR China
Qun Li
Affiliation:
MNR Key Laboratory for Polar Science, Polar Research Institute of China, Shanghai 200136, PR China
Jing Meng
Affiliation:
Key Laboratory of Physical Oceanography, Ocean University of China and Qingdao National Laboratory for Marine Science and Technology, Qingdao 266100, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

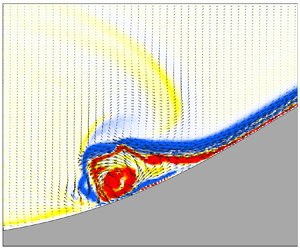
The breaking and energy distribution of mode-1 depression internal solitary wave interactions with Gaussian ridges are examined through laboratory experiments. A series of processes, such as shoaling, breaking, transmission and reflection, are captured completely by measuring the velocity field in a large region. It is found that the maximum interface descent ($a_{max}$) during wave shoaling is an important parameter for diagnosing the type of wave–ridge interaction and energy distribution. The wave breaking on the ridge depends on the modified blockage parameter $\zeta _m$, the ratio of the sum of the upper layer depth and $a_{max}$ to the water depth at the top of the ridge. As $\zeta _m$ increases, the interaction type transitions from no breaking to plunging and mixed plunging–collapsing breaking. Within the scope of this experiment, the energy distribution can be characterized solely by $\zeta _m$. The transmission energy decreases monotonically with increasing $\zeta _m$, and there is a linear relationship between $\zeta _m^2$ and the reflection coefficient. The value of $a_{max}$ can be determined from the basic initial parameters of the experiment. Based on the incident wave parameters, the depth of the upper and lower layers, and the topographic parameters, two new simple methods for predicting $a_{max}$ on the ridge are proposed.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A79
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aghsaee, P. & Boegman, L. 2015 Experimental investigation of sediment resuspension beneath internal solitary waves of depression. J. Geophys. Res.: Oceans 120 (5), 3301–3314.CrossRefGoogle Scholar
Aghsaee, P., Boegman, L. & Lamb, K.G. 2010 Breaking of shoaling internal solitary waves. J. Fluid Mech. 659, 289–317.CrossRefGoogle Scholar
Alford, M.H., Lien, R.C., Simmons, H., Klymak, J., Ramp, S., Yang, Y.J., Tang, D. & Chang, M.H. 2010 Speed and evolution of nonlinear internal waves transiting the South China Sea. J. Phys. Oceanogr. 40 (6), 1338–1355.CrossRefGoogle Scholar
Arthur, R.S. & Fringer, O.B. 2014 The dynamics of breaking internal solitary waves on slopes. J. Fluid Mech. 761, 360–398.CrossRefGoogle Scholar
Bai, X., Liu, Z., Zheng, Q., Hu, J., Lamb, K.G. & Cai, S. 2019 Fission of shoaling internal waves on the northeastern shelf of the South China Sea. J. Geophys. Res.: Oceans 124 (7), 4529–4545.CrossRefGoogle Scholar
Barad, M.F. & Fringer, O.B. 2010 Simulations of shear instabilities in interfacial gravity waves. J. Fluid Mech. 644, 61–95.CrossRefGoogle Scholar
Boegman, L., Ivey, G.N. & Imberger, J. 2005 The degeneration of internal waves in lakes with sloping topography. Limnol. Oceanogr. 50 (5), 1620–1637.CrossRefGoogle Scholar
Boegman, L. & Stastna, M. 2019 Sediment resuspension and transport by internal solitary waves. Annu. Rev. Fluid Mech. 51 (1), 129–154.CrossRefGoogle Scholar
Bogucki, D. & Garrett, C. 1993 A simple model for the shear-induced decay of an internal solitary wave. J. Phys. Oceanogr. 23 (8), 1767–1776.2.0.CO;2>CrossRefGoogle Scholar
Bourgault, D., Janes, D.C. & Galbraith, P.S. 2011 Observations of a large-amplitude internal wave train and its reflection off a steep slope. J. Phys. Oceanogr. 41 (3), 586–600.CrossRefGoogle Scholar
Bourgault, D. & Kelley, D.E. 2003 Wave-induced boundary mixing in a partially mixed estuary. J. Mar. Res. 61 (5), 553–576.CrossRefGoogle Scholar
Bourgault, D. & Kelley, D.E. 2007 On the reflectance of uniform slopes for normally incident interfacial solitary waves. J. Phys. Oceanogr. 37 (5), 1156–1162.CrossRefGoogle Scholar
Cacchione, D.A., Pratson, L.F. & Ogston, A.S. 2002 The shaping of continental slopes by internal tides. Science 296 (5568), 724–727.CrossRefGoogle ScholarPubMed
Carr, M., Franklin, J., King, S.E., Davies, P.A., Grue, J. & Dritschel, D.G. 2017 The characteristics of billows generated by internal solitary waves. J. Fluid Mech. 812, 541–577.CrossRefGoogle Scholar
Carr, M., King, S.E. & Dritschel, D.G. 2011 Numerical simulation of shear-induced instabilities in internal solitary waves. J. Fluid Mech. 683, 263–288.CrossRefGoogle Scholar
Carr, M., Stastna, M., Davies, P.A. & van de Wal, K.J. 2019 Shoaling mode-2 internal solitary-like waves. J. Fluid Mech. 879, 604–632.CrossRefGoogle Scholar
Cavaliere, D., la Forgia, G., Adduce, C., Alpers, W., Martorelli, E. & Falcini, F. 2021 Breaking location of internal solitary waves over a sloping seabed. J. Geophys. Res.: Oceans 126 (2), e2020JC016669.CrossRefGoogle Scholar
Chang, M.-H., et al. 2021 Direct measurements reveal instabilities and turbulence within large amplitude internal solitary waves beneath the ocean. Commun. Earth Environ. 2 (1), 15.CrossRefGoogle Scholar
Chen, C.-Y. 2007 An experimental study of stratified mixing caused by internal solitary waves in a two-layered fluid system over variable seabed topography. Ocean Engineering 34 (14–15), 1995–2008.CrossRefGoogle Scholar
Chen, C.-Y. 2009 Amplitude decay and energy dissipation due to the interaction of internal solitary waves with a triangular obstacle in a two-layer fluid system: the blockage parameter. J. Mar. Sci. Technol. 14 (4), 499–512.CrossRefGoogle Scholar
Chen, C.-Y. 2010 Using discriminant analysis to determine the breaking criterion for an ISW propagating over a ridge. Environ. Fluid Mech. 10 (5), 577–586.CrossRefGoogle Scholar
Cowen, E.A. & Monismith, S.G. 1997 A hybrid digital particle tracking velocimetry technique. Exp. Fluids 22 (3), 199–211.CrossRefGoogle Scholar
Dalziel, S.B., Carr, M., Sveen, J.K. & Davies, P.A. 2007 Simultaneous synthetic schlieren and PIV measurements for internal solitary waves. Meas. Sci. Technol. 18 (3), 533–547.CrossRefGoogle Scholar
Davis, K.A., Arthur, R.S., Reid, E.C., Rogers, J.S., Fringer, O.B., DeCarlo, T.M. & Cohen, A.L. 2020 Fate of internal waves on a shallow shelf. J. Geophys. Res.: Oceans 125 (5), e2019JC015377.CrossRefGoogle Scholar
Deepwell, D., Stastna, M., Carr, M. & Davies, P.A. 2017 Interaction of a mode-2 internal solitary wave with narrow isolated topography. Phys. Fluids 29 (7), 076601.CrossRefGoogle Scholar
Deepwell, D., Stastna, M., Carr, M. & Davies, P.A. 2019 Wave generation through the interaction of a mode-2 internal solitary wave and a broad, isolated ridge. Phys. Rev. Fluids 4 (9), 094802.CrossRefGoogle Scholar
Doron, P., Bertuccioli, L., Katz, J. & Osborn, T.R. 2001 Turbulence characteristics and dissipation estimates in the coastal ocean bottom boundary layer from PIV data. J. Phys. Oceanogr. 31 (8), 2108–2134.2.0.CO;2>CrossRefGoogle Scholar
Dorostkar, A., Boegman, L. & Pollard, A. 2017 Three-dimensional simulation of high-frequency nonlinear internal wave dynamics in Cayuga Lake. J. Geophys. Res.: Oceans 122 (3), 2183–2204.CrossRefGoogle Scholar
Farmer, D., Alford, M., Lien, R.-C., Yang, Y.J., Chang, M.-H. & Li, Q. 2011 From Luzon Strait to Dongsha Plateau: stages in the life of an internal wave. Oceanography 24 (4), 64–77.CrossRefGoogle Scholar
Fritts, D.C., Wang, L., Geller, M.A., Lawrence, D.A., Werne, J. & Balsley, B.B. 2016 Numerical modeling of multiscale dynamics at a high Reynolds number: instabilities, turbulence, and an assessment of Ozmidov and Thorpe scales. J. Atmos. Sci. 73 (2), 555–578.CrossRefGoogle Scholar
Fructus, D., Carr, M., Grue, J., Jensen, A. & Davies, P.A. 2009 Shear-induced breaking of large internal solitary waves. J. Fluid Mech. 620, 1–29.CrossRefGoogle Scholar
Ghassemi, A., Zahedi, S. & Boegman, L. 2021 Bolus formation from fission of nonlinear internal waves over a mild slope. J. Fluid Mech. 932, A50.Google Scholar
Grimshaw, R., Pelinovsky, E., Talipova, T. & Kurkina, O. 2010 Internal solitary waves: propagation, deformation and disintegration. Nonlinear Process. Geophys. 17 (6), 633–649.CrossRefGoogle Scholar
Grimshaw, R.H.J., Ostrovsky, L.A., Shrira, V.I. & Stepanyants, Y.A. 1998 Long nonlinear surface and internal gravity waves in a rotating ocean. Surv. Geophys. 19 (4), 289–338.CrossRefGoogle Scholar
Harnanan, S., Soontiens, N. & Stastna, M. 2015 Internal wave boundary layer interaction: a novel instability over broad topography. Phys. Fluids 27 (1), 016605.CrossRefGoogle Scholar
Harnanan, S., Stastna, M. & Soontiens, N. 2017 The effects of near-bottom stratification on internal wave induced instabilities in the boundary layer. Phys. Fluids 29 (1), 016602.CrossRefGoogle Scholar
Hartharn-Evans, S.G., Carr, M., Stastna, M. & Davies, P.A. 2021 Stratification effects on shoaling internal solitary waves. J. Fluid Mech. 933, A19.Google Scholar
Helfrich, K.R. 1992 Internal solitary wave breaking and run-up on a uniform slope. J. Fluid Mech. 243, 133–154.CrossRefGoogle Scholar
Helfrich, K.R. & Melville, W.K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38 (1), 395–425.CrossRefGoogle Scholar
Hogg, A.M.C. & Ivey, G.N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flows. J. Fluid Mech. 477, 339–362.CrossRefGoogle Scholar
Hsieh, C.-M., Hwang, R.R., Hsu, J.R.C. & Cheng, M.-H. 2015 Numerical modeling of flow evolution for an internal solitary wave propagating over a submerged ridge. Wave Motion 55, 48–72.CrossRefGoogle Scholar
Huang, X., Chen, Z., Zhao, W., Zhang, Z., Zhou, C., Yang, Q. & Tian, J. 2016 An extreme internal solitary wave event observed in the northern South China Sea. Sci. Rep. 6, 30041.CrossRefGoogle ScholarPubMed
Hult, E.L., Troy, C.D. & Koseff, J.R. 2011 The mixing efficiency of interfacial waves breaking at a ridge: 1. Overall mixing efficiency. J. Geophys. Res. 116 (C2), 2010JC006485.Google Scholar
Jackson, C. 2007 Internal wave detection using the moderate resolution imaging spectroradiometer (MODIS). J. Geophys. Res. 112 (C11), C11012.Google Scholar
Jones, N.L., Ivey, G.N., Rayson, M.D. & Kelly, S.M. 2020 Mixing driven by breaking nonlinear internal waves. Geophys. Res. Lett. 47 (19), e2020GL089591.CrossRefGoogle Scholar
Kao, T.W., Pan, F.-S. & Renouard, D. 1985 Internal solitons on the pycnocline: generation, propagation, and shoaling and breaking over a slope. J. Fluid Mech. 159, 19–53.CrossRefGoogle Scholar
Kunze, E. & Sanford, T.B. 1996 Abyssal mixing: where it is not. J. Phys. Oceanogr. 26 (10), 2286–2296.2.0.CO;2>CrossRefGoogle Scholar
La Forgia, G., Adduce, C. & Falcini, F. 2018 Laboratory investigation on internal solitary waves interacting with a uniform slope. Adv. Water Resour. 120, 4–18.CrossRefGoogle Scholar
Lamb, K.G. 2002 A numerical investigation of solitary internal waves with trapped cores formed via shoaling. J. Fluid Mech. 451, 109–144.CrossRefGoogle Scholar
Lamb, K.G. 2003 Shoaling solitary internal waves: on a criterion for the formation of waves with trapped cores. J. Fluid Mech. 478, 81–100.CrossRefGoogle Scholar
Lamb, K.G. 2014 Internal wave breaking and dissipation mechanisms on the continental slope/shelf. Annu. Rev. Fluid Mech. 46 (1), 231–254.CrossRefGoogle Scholar
Lamb, K.G. & Farmer, D. 2011 Instabilities in an internal solitary-like wave on the Oregon Shelf. J. Phys. Oceanogr. 41 (1), 67–87.CrossRefGoogle Scholar
Lamb, K.G. & Nguyen, V.T. 2009 Calculating energy flux in internal solitary waves with an application to reflectance. J. Phys. Oceanogr. 39 (3), 559–580.CrossRefGoogle Scholar
Liao, Q., Bootsma, H.A., Xiao, J., Klump, J.V., Hume, A., Long, M.H. & Berg, P. 2009 Development of an in situ underwater particle image velocimetry (UWPIV) system. Limnol. Oceanogr.: Methods 7 (2), 169–184.CrossRefGoogle Scholar
Lien, R.C., Henyey, F., Ma, B. & Yang, Y.J. 2014 Large-amplitude internal solitary waves observed in the northern South China Sea: properties and energetics. J. Phys. Oceanogr. 44 (4), 1095–1115.CrossRefGoogle Scholar
Lin, Y.-T., Luo, Y., Yu, J., Song, J. & Yuan, Y. 2021 Laboratory investigation of turbulent dissipation in an internal solitary wave breaking over a submerged Gaussian ridge. Phys. Fluids 33 (9), 096602.CrossRefGoogle Scholar
Maderich, V., Talipova, T., Grimshaw, R., Terletska, K., Brovchenko, I., Pelinovsky, E. & Choi, B.H. 2010 Interaction of a large amplitude interfacial solitary wave of depression with a bottom step. Phys. Fluids 22 (7), 076602.CrossRefGoogle Scholar
Michallet, H. & Ivey, G.N. 1999 Experiments on mixing due to internal solitary waves breaking on uniform slopes. J. Geophys. Res.: Oceans 104 (C6), 13467–13477.CrossRefGoogle Scholar
Moum, J.N., Farmer, D.M., Smyth, W.D., Armi, L. & Vagle, S. 2003 Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf. J. Phys. Oceanogr. 33 (10), 2093–2112.2.0.CO;2>CrossRefGoogle Scholar
Nakayama, K., Sato, T., Shimizu, K. & Boegman, L. 2019 Classification of internal solitary wave breaking over a slope. Phys. Rev. Fluids 4 (1), 014801.CrossRefGoogle Scholar
Orr, M.H. & Mignerey, P.C. 2003 Nonlinear internal waves in the South China Sea: observation of the conversion of depression internal waves to elevation internal waves. J. Geophys. Res. Oceans 108 (C3), 3064.CrossRefGoogle Scholar
Pinkel, R. 2000 Internal solitary waves in the warm pool of the western equatorial Pacific. J. Phys. Oceanogr. 30 (11), 2906–2926.2.0.CO;2>CrossRefGoogle Scholar
Raffel, M. 2015 Background-oriented schlieren (BOS) techniques. Exp. Fluids 56 (3), 60.CrossRefGoogle Scholar
Ramp, S.R., Park, J.H., Yang, Y.J., Bahr, F.L. & Jeon, C. 2019 Latitudinal structure of solitons in the South China Sea. J. Phys. Oceanogr. 49 (7), 1747–1767.CrossRefGoogle Scholar
Ramp, S.R., Yang, Y.-J., Jan, S., Chang, M.-H., Davis, K.A., Sinnett, G., Bahr, F.L., Reeder, D.B., Ko, D.S. & Pawlak, G. 2022 Solitary waves impinging on an isolated tropical reef: arrival patterns and wave transformation under shoaling. J. Geophys. Res.: Oceans 127 (3), e2021JC017781.CrossRefGoogle Scholar
Reeder, D.B., Ma, B.B. & Yang, Y.J. 2011 Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves. Mar. Geol. 279 (1–4), 12–18.CrossRefGoogle Scholar
Rivera-Rosario, G., Diamessis, P.J., Lien, R.-C., Lamb, K.G. & Thomsen, G.N. 2020 Formation of recirculating cores in convectively breaking internal solitary waves of depression shoaling over gentle slopes in the South China Sea. J. Phys. Oceanogr. 50 (5), 1137–1157.CrossRefGoogle Scholar
Rivera-Rosario, G., Diamessis, P.J., Lien, R.-C., Lamb, K.G. & Thomsen, G.N. 2022 Three-dimensional perspective on a convective instability and transition to turbulence in an internal solitary wave of depression shoaling over gentle slopes. Environ. Fluid Mech. 23, 1015–1035.Google Scholar
Sandstrom, H. & Elliott, J.A. 1984 Internal tide and solitons on the Scotian Shelf: a nutrient pump at work. J. Geophys. Res. 89 (C4), 6415–6426.Google Scholar
Settles, G.S. & Hargather, M.J. 2017 A review of recent developments in schlieren and shadowgraph techniques. Meas. Sci. Technol. 28 (4), 042001.CrossRefGoogle Scholar
Sinnett, G., Ramp, S.R., Yang, Y.J., Chang, M.-H., Jan, S. & Davis, K.A. 2022 Large-amplitude internal wave transformation into shallow water. J. Phys. Oceanogr. 52 (10), 2539–2554.CrossRefGoogle Scholar
Smith, D.K. 1988 Shape analysis of Pacific seamounts. Earth Planet. Sci. Lett. 90 (4), 457–466.CrossRefGoogle Scholar
Song, Z.J., Teng, B., Gou, Y., Lu, L., Shi, Z.M., Xiao, Y. & Qu, Y. 2011 Comparisons of internal solitary wave and surface wave actions on marine structures and their responses. Appl. Ocean Res. 33 (2), 120–129.CrossRefGoogle Scholar
Sutherland, B.R., Barrett, K.J. & Ivey, G.N. 2013 Shoaling internal solitary waves. J. Geophys. Res.: Oceans 118 (9), 4111–4124.CrossRefGoogle Scholar
Sutherland, B.R., Keating, S. & Shrivastava, I. 2015 Transmission and reflection of internal solitary waves incident upon a triangular barrier. J. Fluid Mech. 775, 304–327.CrossRefGoogle Scholar
Sveen, J.K., Guo, Y., Davies, P.A. & Grue, J. 2002 On the breaking of internal solitary waves at a ridge. J. Fluid Mech. 469, 161–188.CrossRefGoogle Scholar
Talipova, T.G., Kurkina, O.E., Rouvinskaya, E.A. & Pelinovsky, E.N. 2015 Propagation of solitary internal waves in two-layer ocean of variable depth. Izv. Atmos. Ocean. Phys. 51 (1), 89–97.CrossRefGoogle Scholar
Thielicke, W. 2014 The flapping flight of birds: analysis and application. PhD thesis, University of Groningen.Google Scholar
Thielicke, W. & Sonntag, R. 2021 Particle image velocimetry for MATLAB: accuracy and enhanced algorithms in PIVlab. J. Open Res. Softw. 9 (1), 12.CrossRefGoogle Scholar
Thielicke, W. & Stamhuis, E.J. 2014 PIVlab – towards user-friendly, affordable and accurate digital particle image velocimetry in MATLAB. J. Open Res. Softw. 2 (1), 30.CrossRefGoogle Scholar
Toole, J.M., Schmitt, R.W., Polzin, K.L. & Kunze, E. 1997 Near-boundary mixing above the flanks of a midlatitude seamount. J. Geophys. Res.: Oceans 102 (C1), 947–959.CrossRefGoogle Scholar
Vlasenko, V. 2005 Generation of secondary internal waves by the interaction of an internal solitary wave with an underwater bank. J. Geophys. Res. 110 (C2), C02019.Google Scholar
Vlasenko, V. & Hutter, K. 2002 Numerical experiments on the breaking of solitary internal waves over a slope–shelf topography. J. Phys. Oceanogr. 32 (6), 1779–1793.2.0.CO;2>CrossRefGoogle Scholar
Wallace, B.C. & Wilkinson, D.L. 1988 Run-up of internal waves on a gentle slope in a two-layered system. J. Fluid Mech. 191, 419–442.CrossRefGoogle Scholar
Wang, T., Huang, X., Zhao, W., Zheng, S., Yang, Y. & Tian, J. 2022 Internal solitary wave activities near the Indonesian submarine wreck site inferred from satellite images. J. Mar. Sci. Engng 10 (2), 197.Google Scholar
Wang, X., Zhou, J.-F., Wang, Z. & You, Y.-X. 2018 A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean Engng 150, 298–308.CrossRefGoogle Scholar
Wessel, P. 2001 Global distribution of seamounts inferred from gridded Geosat/ERS-1 altimetry. J. Geophys. Res.: Solid Earth 106 (B9), 19431–19441.CrossRefGoogle Scholar
Wessels, F. & Hutter, K. 1996 Interaction of internal waves with a topographic sill in a two-layered fluid. J. Phys. Oceanogr. 26 (1), 5–20.2.0.CO;2>CrossRefGoogle Scholar
Xie, J., He, Y. & Cai, S. 2019 Bumpy topographic effects on the transbasin evolution of large-amplitude internal solitary wave in the northern South China Sea. J. Geophys. Res.: Oceans 124 (7), 4677–4695.CrossRefGoogle Scholar
Xu, C. 2015 Numerical simulations of shoaling internal solitary waves of elevation. PhD thesis, University of Waterloo.CrossRefGoogle Scholar
Xu, C. & Stastna, M. 2020 Instability and cross-boundary-layer transport by shoaling internal waves over realistic slopes. J. Fluid Mech. 895, R6.CrossRefGoogle Scholar
Xu, C., Stastna, M. & Deepwell, D. 2019 Spontaneous instability in internal solitary-like waves. Phys. Rev. Fluids 4, 014805.CrossRefGoogle Scholar
Yang, Y.J., Fang, Y.C., Tang, T.Y. & Ramp, S.R. 2010 Convex and concave types of second baroclinic mode internal solitary waves. Nonlinear Process. Geophys. 17 (6), 605–614.CrossRefGoogle Scholar
Zahedi, S. 2021 Energy dissipation from internal solitary waves shoaling on flat and mildly sloping beds. PhD thesis, Queen's University.Google Scholar
Zhang, X., Huang, X., Yang, Y., Zhao, W., Wang, H., Yuan, C. & Tian, J. 2023 Energy cascade from internal solitary waves to turbulence via near-$N$ waves in the northern South China Sea. J. Phys. Oceanogr. 53 (6), 1453–1466.CrossRefGoogle Scholar
Zhao, Z., Klemas, V.V., Zheng, Q. & Yan, X.-H. 2003 Satellite observation of internal solitary waves converting polarity. Geophys. Res. Lett. 30 (19), 1988.CrossRefGoogle Scholar
Zhu, H., Wang, L., Avital, E.J., Tang, H. & Williams, J.J.R. 2016 Numerical simulation of interaction between internal solitary waves and submerged ridges. Appl. Ocean Res. 58, 118–134.CrossRefGoogle Scholar
Supplementary material: File

Guo et al. supplementary material

Guo et al. supplementary material
Download Guo et al. supplementary material(File)
File 1.5 MB