Article contents
Kinks on elliptical convergent shock waves in hypersonic flow
Published online by Cambridge University Press: 12 December 2023
Abstract
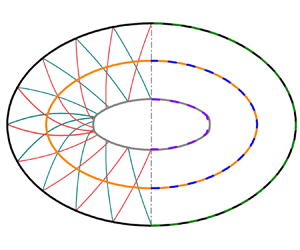
Kinks commonly appear on the convergent shock surface when an internal conical flow deviates from the axisymmetric state. In this paper, the formation mechanisms of kinks on internal conical shocks (ICSs) generated by elliptical ring wedges with typical entry aspect ratios ( $AR{\rm s}$) in a Mach 6 flow are revealed using a theoretical method, in which the spatial evolution of the three-dimensional elliptical ICS is converted into a temporal evolution of a two-dimensional elliptical moving shock (EMS) using the hypersonic equivalence principle. To simultaneously track the shock front of the EMS and the disturbances propagating along it, a front-disturbance tracking method (FDTM) based on geometrical shock dynamics is proposed. It is found that the shock–compression disturbances from the same family initially near the major axis catch up with the disturbance initially emitted from the major axis to form kinks on the EMS. The equivalent kink formation positions predicted by the FDTM always lag behind the real kink formation positions on the elliptical ICS because the applicability of the hypersonic equivalence principle decays as the shock strengthens along the incoming flow direction. The accuracy of the equivalent kink formation positions predicted by the FDTM gradually declines with the reduction in
$AR{\rm s}$) in a Mach 6 flow are revealed using a theoretical method, in which the spatial evolution of the three-dimensional elliptical ICS is converted into a temporal evolution of a two-dimensional elliptical moving shock (EMS) using the hypersonic equivalence principle. To simultaneously track the shock front of the EMS and the disturbances propagating along it, a front-disturbance tracking method (FDTM) based on geometrical shock dynamics is proposed. It is found that the shock–compression disturbances from the same family initially near the major axis catch up with the disturbance initially emitted from the major axis to form kinks on the EMS. The equivalent kink formation positions predicted by the FDTM always lag behind the real kink formation positions on the elliptical ICS because the applicability of the hypersonic equivalence principle decays as the shock strengthens along the incoming flow direction. The accuracy of the equivalent kink formation positions predicted by the FDTM gradually declines with the reduction in  $AR$, but it can be significantly improved for all
$AR$, but it can be significantly improved for all  $AR{\rm s}$ after a modification of the equivalent relationship using the shock angle in the major plane of the elliptical ICS, which provides a new way to solve the kinks on the elliptical ICS.
$AR{\rm s}$ after a modification of the equivalent relationship using the shock angle in the major plane of the elliptical ICS, which provides a new way to solve the kinks on the elliptical ICS.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 2
- Cited by



