Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-29T04:37:08.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Kazantsev model in non-helical 2.5-dimensional flows

Published online by Cambridge University Press:  13 October 2016

K. Seshasayanan Open the ORCID record for K. Seshasayanan [Opens in a new window]  and
A. Alexakis
K. Seshasayanan*
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, PSL Research University; Université Paris Diderot Sorbonne Paris-Cité; Sorbonne Universités UPMC Univ Paris 06; CNRS; 24 rue Lhomond, 75005 Paris, France
A. Alexakis
Affiliation:
Laboratoire de Physique Statistique, École Normale Supérieure, PSL Research University; Université Paris Diderot Sorbonne Paris-Cité; Sorbonne Universités UPMC Univ Paris 06; CNRS; 24 rue Lhomond, 75005 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamo instability for a Kazantsev–Kraichnan flow with three velocity components that depend only on two dimensions 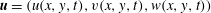$\boldsymbol{u}=(u(x,y,t),v(x,y,t),w(x,y,t))$ often referred to as 2.5-dimensional (2.5-D) flow. Within the Kazantsev–Kraichnan framework we derive the governing equations for the second-order magnetic field correlation function and examine the growth rate of the dynamo instability as a function of the control parameters of the system. In particular we investigate the dynamo behaviour for large magnetic Reynolds numbers 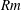$Rm$ and flows close to being two-dimensional and show that these two limiting procedures do not commute. The energy spectra of the unstable modes are derived analytically and lead to power-law behaviour that differs from the three-dimensional and two-dimensional cases. The results of our analytical calculation are compared with the results of numerical simulations of dynamos driven by prescribed fluctuating flows as well as freely evolving turbulent flows, showing good agreement.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD and Electrohydrodynamics MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 627 - 648
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boldyrev, S. 2001 A solvable model for nonlinear mean field dynamo. Astrophys. J. 562 (2), 1081.Google Scholar
Boldyrev, S., Cattaneo, F. & Rosner, R. 2005 Magnetic-field generation in helical turbulence. Phys. Rev. Lett. 95 (25), 255001.Google Scholar
Boldyrev, S. A. & Schekochihin, A. A. 2000 Geometric properties of passive random advection. Phys. Rev. E 62 (1), 545.Google Scholar
Chatfield, C. 1989 The Analysis of Time Series an Introduction. Chapman and Hall.Google Scholar
Chertkov, M., Falkovich, G., Kolokolov, I. & Vergassola, M. 1999 Small-scale turbulent dynamo. Phys. Rev. Lett. 83 (20), 4065.CrossRefGoogle Scholar
Falkovich, G., Gawdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73 (4), 913.Google Scholar
Furutsu, K. 1963 On the statistical theory of electromagnetic waves in a fluctuating medium (i). J. Res. Natl Bur. Stand. 67D, 303.Google Scholar
Galloway, D. J. & Proctor, M. R. E. 1992 Numerical calculations of fast dynamos in smooth velocity fields with realistic diffusion. Nature 356, 691–693.Google Scholar
Greiner, A., Strittmatter, W. & Honerkamp, J. 1988 Numerical integration of stochastic differential equations. J. Stat. Phys. 51 (1–2), 95–108.CrossRefGoogle Scholar
Iskakov, A. B., Schekochihin, A. A., Cowley, S. C., Mcwilliams, J. C. & Proctor, M. R. E. 2007 Numerical demonstration of fluctuation dynamo at low magnetic Prandtl numbers. Phys. Rev. Lett. 98 (20), 208501.Google Scholar
Kazantsev, A. P. 1968 Enhancement of a magnetic field by a conducting fluid. Sov. Phys. JETP 26 (5), 1031–1034.Google Scholar
Kolokolov, I.2016 Kinematic dynamo in two-dimensional chaotic flow: the initial and final stages. arXiv:1603:08771.Google Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11 (5), 945–953.Google Scholar
Leprovost, N.2004, Influence des petites échelles sur la dynamique à grande échelle en turbulence hydro et magnétohydrodynamique. PhD thesis, Université Pierre et Marie Curie-Paris VI.Google Scholar
Malyshkin, L. M. & Boldyrev, S. 2010 Magnetic dynamo action at low magnetic Prandtl numbers. Phys. Rev. Lett. 105 (21), 215002.Google Scholar
Mason, J., Malyshkin, L., Boldyrev, S. & Cattaneo, F. 2011 Magnetic dynamo action in random flows with zero and finite correlation times. Astrophys. J. 730 (2), 86.Google Scholar
Novikov, E. A. 1965 Functionals and the random-force method in turbulence theory. Sov. Phys. JETP 20 (5), 1290–1294.Google Scholar
Novikov, V. G., Ruzmaikin, A. A. & Sokoloff, D. D. 1983 Kinematic dynamo in a reflection-invariant random field. Sov. Phys. JETP 58, 527–532.Google Scholar
Oughton, S., Rädler, K. H. & Matthaeus, W. H. 1997 General second-rank correlation tensors for homogeneous magnetohydrodynamic turbulence. Phys. Rev. E 56 (3), 2875.Google Scholar
Proudman, J. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92 (642), 408–424.Google Scholar
Roberts, G. O. 1972 Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. R. Soc. 271 (1216), 411–454.Google Scholar
Ruzmaikin, A. A. & Sokolov, D. D. 1981 The magnetic field in mirror-invariant turbulence. Sov. Astron. Lett. 7, 388–390.Google Scholar
Schekochihin, A. A., Boldyrev, S. A. & Kulsrud, R. M. 2002 Spectra and growth rates of fluctuating magnetic fields in the kinematic dynamo theory with large magnetic Prandtl numbers. Astrophys. J. 567 (2), 828.Google Scholar
Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L. & Mcwilliams, J. C. 2004 Simulations of the small-scale turbulent dynamo. Astrophys. J. 612 (1), 276.Google Scholar
Seshasayanan, K. & Alexakis, A. 2016 Turbulent 2.5-dimensional dynamos. J. Fluid Mech. 799, 246–264.Google Scholar
Smith, S. G. L. & Tobias, S. M. 2004 Vortex dynamos. J. Fluid Mech. 498, 1–21.CrossRefGoogle Scholar
Subramanian, K. 1999 Unified treatment of small-and large-scale dynamos in helical turbulence. Phys. Rev. Lett. 83 (15), 2957.CrossRefGoogle Scholar
Taylor, Go. I. 1917 Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. A 93 (648), 99–113.Google Scholar
Tobias, S. M. & Cattaneo, F. 2008 Dynamo action in complex flows: the quick and the fast. J. Fluid Mech. 601, 101–122.Google Scholar
Vincenzi, D. 2002 The Kraichnan–Kazantsev dynamo. J. Stat. Phys. 106 (5–6), 1073–1091.Google Scholar
Zeldovich, Y. B. 1957 The magnetic field in the two-dimensional motion of a conducting turbulent fluid. Sov. Phys. JETP 4, 460–462.Google Scholar