Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T06:42:13.608Z Has data issue: false hasContentIssue false
  • English
  • Français

A k–ε turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows

Published online by Cambridge University Press:  09 May 2012

A. T. King ,
R. O. Tinoco  and
E. A. Cowen
A. T. King*
Affiliation:
DeFrees Hydraulics Laboratory, Department of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
R. O. Tinoco
Affiliation:
DeFrees Hydraulics Laboratory, Department of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
E. A. Cowen
Affiliation:
DeFrees Hydraulics Laboratory, Department of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

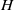Flow and transport through aquatic vegetation is characterized by a wide range of length scales: water depth (), plant height (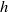), stem diameter (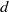), the inverse of the plant frontal area per unit volume () and the scale(s) over which varies. Turbulence is generated both at the scale(s) of the mean vertical shear, set in part by , and at the scale(s) of the stem wakes, set by 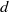. While turbulence from each of these sources is dissipated through the energy cascade, some shear-scale turbulence bypasses the lower wavenumbers as shear-scale eddies do work against the form drag of the plant stems, converting shear-scale turbulence into wake-scale turbulence. We have developed a 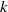– model that accounts for all of these energy pathways. The model is calibrated against laboratory data from beds of rigid cylinders under emergent and submerged conditions and validated against an independent data set from submerged rigid cylinders and a laboratory data set from a canopy of live vegetation. The new model outperforms existing 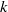– models, none of which include the 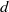scale, both in the emergent rigid cylinder case, where existing – models break down entirely, and in the submerged rigid cylinder and live plant cases, where existing 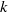– models fail to predict the strong dependence of turbulent kinetic energy on . The new model is limited to canopies dense enough that dispersive fluxes are negligible.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Turbulent Flows: Turbulence modelling Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 1 - 39
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Blumberg, A. F. & Mellor, G. L. 1987 A description of a three-dimensional coastal ocean circulation model. In Three-dimensional Coastal Ocean Models (ed. Heaps, N. ). American Geophysical Union.CrossRefGoogle Scholar
2. Bohm, M., Finnigan, J. J. & Raupach, M. R. 2000 Dispersive fluxes and canopy flows: just how important are they? In American Meteorological Society, 24th Conference on Agricultural and Forest Meteorology, University of California, Davis, 14–18 August 2000, pp. 106–107.Google Scholar
3. Burchard, H. & Peterson, O. 1999 Models of turbulence in the marine environment – a comparative study of two-equation turbulence models. J. Mar. Syst. 21, 29–53.CrossRefGoogle Scholar
4. Cava, D. & Katul, G. G. 2008 Spectal short-circuiting and wake production within the canopy trunk space of an Alpine hardwood forest. Boundary-Layer Meteorol. 126, 415–431.CrossRefGoogle Scholar
5. Coceal, O. & Belcher, S. E. 2004 A canopy model of mean winds through urban areas. Q. J. R. Meteorol. Soc. 130, 1349–1372.CrossRefGoogle Scholar
6. Cowen, E. & Monismith, S. 1997 A hybrid digital particle tracking velocimetry technique. Exp. Fluids 22, 199–211.CrossRefGoogle Scholar
7. Dunn, C., López, F. & García, M. 1996 Mean flow and turbulence in a laboratory channel with simulated vegetation. Hydraul. Eng. Ser. 51, UILU-ENG-96-2009, Department of Civil Engineering, University of Illinois at Urbana-Champaign, Urbana, IL.Google Scholar
8. Efron, B. R. & Tibshirani, R. 1993 An Introduction to the Bootstrap. Chapman & Hall.CrossRefGoogle Scholar
9. Finnemore, E. J. & Franzini, J. B. 2002 Fluid Mechanics with Engineering Applications, 10th edn. McGraw-Hill Higher Education.Google Scholar
10. Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32, 519–571.CrossRefGoogle Scholar
11. Finnigan, J. J. 1985 Turbulent transport in flexible plant canopies. In The Forest–Atmosphere Interaction (ed. Hutchison, B. A. & Hicks, B. B. ), pp. 443–480. D. Reidel.CrossRefGoogle Scholar
12. Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
13. Ghisalberti, M. 2009 Obstructed shear flows: similarities across systems and scales. J. Fluid Mech. 641, 51–61.CrossRefGoogle Scholar
14. Ghisalberti, M. & Nepf, H. M. 2004 The limited growth of vegetated shear layers. Water Resour. Res. 40, W07502, 1–12.CrossRefGoogle Scholar
15. Katul, G. G., Mahrt, L., Poggi, D. & Sanz, C. 2004 One- and two-equation models for canopy turbulence. Boundary-Layer Meteorol. 113, 81–109.CrossRefGoogle Scholar
16. King, A. T., Rueda, F. J., Tinoco, R. O. & Cowen, E. A. 2009 Modeling flow and transport through aquatic vegetation in natural water bodies. In Proceedings of the 33rd IAHR Congress, Vancouver, BC, Canada, August 9–14, 2009.Google Scholar
17. Koch, D. & Ladd, A. 1997 Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 349, 31–66.CrossRefGoogle Scholar
18. Launder, B. E. & Spalding, D. B. 1974 The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. 3, 269–289.CrossRefGoogle Scholar
19. Lillie, R. A., Budd, J. & Rasmussen, P. W. 1997 Spatial and temporal variability in biomass density of Myriophyllum spicatum L. in a northern temperate lake. Hydrobiologia 347, 69–74.CrossRefGoogle Scholar
20. Lin, P. & Liu, P. L.-F. 1998 Turbulence transport, vorticity dynamics, and solute mixing under plunging breaking waves in surf zone. J. Geophys. Res. 103, 15677–15694.CrossRefGoogle Scholar
21. López, F. & García, M. H. 2001 Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. J. Hydraul. Engng 127, 392–402.CrossRefGoogle Scholar
22. Luhar, M., Rominger, J. & Nepf, H. 2008 Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 8, 423–439.CrossRefGoogle Scholar
23. Nepf, H., Ghisalberti, M., White, B. & Murphy, E. 2007 Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 43, W04422, 1–10.CrossRefGoogle Scholar
24. Nepf, H. M. & Vivoni, E. R. 2000 Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 105 (C12), 28547–28557.CrossRefGoogle Scholar
25. Nikora, V., McLean, S., Coleman, S., Pokrajac, D., McEwan, I., Campbell, L., Aberle, J., Clunie, D. & Koll, K. 2007 Double-averaging concept for rough-bed open-channel and overland flows: applications. J. Geophys. Res. 133 (8), 884–895.Google Scholar
26. Poggi, D., Katul, G. G. & Albertson, J. D. 2004a Momentum transfer and turbulent kinetic energy budgets within a dense model canopy. Boundary-Layer Meteorol. 111, 589–614.CrossRefGoogle Scholar
27. Poggi, D., Katul, G. G. & Albertson, J. D. 2004b A note on the contribution of dispersive fluxes to momentum transfer within canopies. Boundary-Layer Meteorol. 111, 615–621.CrossRefGoogle Scholar
28. Poggi, D., Katul, G. G., Finnigan, J. J. & Belcher, S. E. 2008 Analytical models for the mean flow inside dense canopies on gentle hilly terrain. Q. J. R. Meteorol. Soc. 134, 1095–1112.CrossRefGoogle Scholar
29. Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004c The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111, 567–587.CrossRefGoogle Scholar
30. Raupach, M. R., Coppin, P. A. & Legg, B. J. 1986 Experiments on scalar dispersion within a model plant canopy. Part I. The turbulence structure. Boundary-Layer Meteorol. 35, 21–52.CrossRefGoogle Scholar
31. Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorol. 22, 79–90.CrossRefGoogle Scholar
32. Rueda, F. J. & Schladow, S. G. 2002 Quantitative comparison of models for the barotropic response of homogeneous basins. J. Hydraul. Engng 128, 201–213.CrossRefGoogle Scholar
33. Shaw, R. H. & Seginer, I. 1985 The dissipation of turbulence in plant canopies. In Proceedings of the 7th Symposium of the American Meteorological Society on Turbulence and Diffusion, pp. 200–203. American Meteorological Society.Google Scholar
34. Smith, P. E. 2006 A semi-implicit, three-dimensional model of estuarine circulation. Tech. Rep. Open file report 2006-1004. USGS, Sacramento, CA.CrossRefGoogle Scholar
35. Song, Y. & Haidvogel, D. 1994 A semi-implicit ocean circulation model using a generalized topography-following coordinate system. J. Comput. Phys. 115, 228–244.CrossRefGoogle Scholar
36. Tanino, Y. & Nepf, H. M. 2008a Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Engng 134, 34–41.CrossRefGoogle Scholar
37. Tanino, Y. & Nepf, H. M. 2008b Lateral dispersion in random cylinder arrays at high Reynolds number. J. Fluid Mech. 600, 339–371.CrossRefGoogle Scholar
38. Tanino, Y. & Nepf, H. M. 2009 Laboratory investigation of lateral dispersion within dense arrays of randomly distributed cylinders at transitional Reynolds number. Phys. Fluids 21, 046603.CrossRefGoogle Scholar
39. Tinoco, R. O. & Cowen, E. A. 2012 The direct measurement of bed stress and drag on individual and random arrays of elements. Exp. Fluids, submitted manuscript.CrossRefGoogle Scholar
40. Tinoco Lopez, R. O. 2008 An experimental investigation of the turbulent flow structure in one-dimensional emergent macrophyte patches. Master’s thesis, Cornell University.Google Scholar
41. Tinoco Lopez, R. O. 2011 An experimental investigation of drag and the turbulent flow structure in simulated and real aquatic vegetation. PhD thesis, Cornell University.Google Scholar
42. Werely, S. & Meinhart, C. 2001 Second-order accurate particle image velocimetry. Exp. Fluids 31, 258–268.CrossRefGoogle Scholar
43. White, F. M. 2011 Fluid Mechanics, 7th edn. McGraw-Hill Higher Education.Google Scholar
44. Wilson, J. D. 1988 A second-order closure model for flow through vegetation. Boundary-Layer Meteorol. 42, 371–392.CrossRefGoogle Scholar
45. Wilson, N. R. & Shaw, R. H. 1977 A higher order closure model for canopy flow. J. Appl. Meteorol. 16, 1197–1205.2.0.CO;2>CrossRefGoogle Scholar
46. Wüest, A. & Lorke, A. 2003 Small-scale hydrodynamics in lakes. Annu. Rev. Fluid Mech. 35, 373–412.CrossRefGoogle Scholar