Published online by Cambridge University Press: 04 November 2014
The linear global instability and resulting transition to turbulence induced by an isolated cylindrical roughness element of height 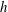 $h$ and diameter
$h$ and diameter 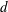 $d$ immersed within an incompressible boundary layer flow along a flat plate is investigated using the joint application of direct numerical simulations and fully three-dimensional global stability analyses. For the range of parameters investigated, base flow computations show that the roughness element induces a wake composed of a central low-speed region surrounded by a three-dimensional shear layer and a pair of low- and high-speed streaks on each of its sides. Results from the global stability analyses highlight the unstable nature of the central low-speed region and its crucial importance in the laminar–turbulent transition process. It is able to sustain two different global instabilities: a sinuous and a varicose one. Each of these globally unstable modes is related to a different physical mechanism. While the varicose mode has its root in the instability of the whole three-dimensional shear layer surrounding the central low-speed region, the sinuous instability turns out to be similar to the von Kármán instability in the two-dimensional cylinder wake and has its root in the lateral shear layers of the separated zone. The aspect ratio of the roughness element plays a key role on the selection of the dominant instability: whereas the flow over thin cylindrical roughness elements transitions due to a sinuous instability of the near-wake region, for larger roughness elements the varicose instability of the central low-speed region turns out to be the dominant one. Direct numerical simulations of the flow past an aspect ratio
$d$ immersed within an incompressible boundary layer flow along a flat plate is investigated using the joint application of direct numerical simulations and fully three-dimensional global stability analyses. For the range of parameters investigated, base flow computations show that the roughness element induces a wake composed of a central low-speed region surrounded by a three-dimensional shear layer and a pair of low- and high-speed streaks on each of its sides. Results from the global stability analyses highlight the unstable nature of the central low-speed region and its crucial importance in the laminar–turbulent transition process. It is able to sustain two different global instabilities: a sinuous and a varicose one. Each of these globally unstable modes is related to a different physical mechanism. While the varicose mode has its root in the instability of the whole three-dimensional shear layer surrounding the central low-speed region, the sinuous instability turns out to be similar to the von Kármán instability in the two-dimensional cylinder wake and has its root in the lateral shear layers of the separated zone. The aspect ratio of the roughness element plays a key role on the selection of the dominant instability: whereas the flow over thin cylindrical roughness elements transitions due to a sinuous instability of the near-wake region, for larger roughness elements the varicose instability of the central low-speed region turns out to be the dominant one. Direct numerical simulations of the flow past an aspect ratio 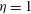 ${\it\eta}=1$ (with
${\it\eta}=1$ (with 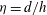 ${\it\eta}=d/h$) roughness element sustaining only the sinuous instability have revealed that the bifurcation occurring in this particular case is supercritical. Finally, comparison of the transition thresholds predicted by global linear stability analyses with the von Doenhoff–Braslow transition diagram provides qualitatively good agreement.
${\it\eta}=d/h$) roughness element sustaining only the sinuous instability have revealed that the bifurcation occurring in this particular case is supercritical. Finally, comparison of the transition thresholds predicted by global linear stability analyses with the von Doenhoff–Braslow transition diagram provides qualitatively good agreement.