Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T12:12:31.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Investigation of the imbibition/drainage of two immiscible fluids in capillaries with arbitrary axisymmetric cross-sections: a generalized model

Published online by Cambridge University Press:  17 August 2022

Amgad Salama Open the ORCID record for Amgad Salama [Opens in a new window]
Amgad Salama*
Affiliation:
Process System Engineering, Faculty of Engineering and Applied Science, University of Regina,Regina, SK S4S 0A2, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

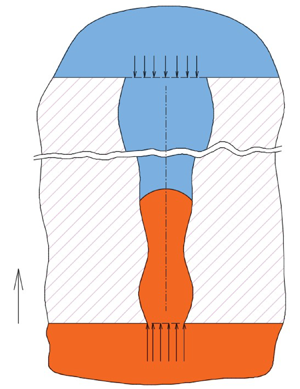
In this work, we investigate the problem of imbibition/drainage of a fluid in capillaries of arbitrary axisymmetric cross-sections filled initially with another immiscible one. The model predicts the location of the meniscus and its speed along the tube length with time. The two immiscible fluids may assume any density and viscosity contrasts. In addition, the axisymmetric profile of the tube maintains a relatively small angle of tangency to warrant that the axial velocity distribution assumes, approximately, a parabolic profile. The driving forces that may be encountered in this system include the capillary force, pressure force, gravitational force and an opposing viscous force. The orientation of the capillary force can be in the direction of the flow (e.g. during imbibition) or opposite to the flow (e.g. during drainage). Likewise, the gravitational force can be in the direction of the flow or opposite to it. In this work we account for all these possibilities. A differential equation is developed that defines the location of the meniscus with time. A fourth-order-accurate Runge–Kutta scheme has been developed to provide solutions for the different scenarios associated with this system. It is shown that the developed model reduces to those appropriate for straight tubes, which builds confidence in the modelling approach. The effects of changing the tangent along the profile of the tube, which influences the calculation of the radius of curvature of the meniscus, is also considered. Unlike the cases of straight capillary tubes, in tubes with arbitrary symmetric profiles, the friction force depends on the variations of the tube profile. Examples of converging/diverging capillary tubes that follow straight and power law profiles are investigated. In addition, the case of sinusoidal profiles has also been considered.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 947 , 25 September 2022 , A12
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashraf, S. & Phirani, J. 2019 a A generalized model for spontaneous imbibition in a horizontal, multi-layered porous medium. Chem. Engng Sci 209, 115175.CrossRefGoogle Scholar
Ashraf, S. & Phirani, J. 2019 b Capillary displacement of viscous liquids in a multi-layered porous medium. Soft Matter 15, 2057–2070.CrossRefGoogle Scholar
Ashraf, S., Visavale, G. & Phirani, J. 2018 Spontaneous imbibition in randomly arranged interacting capillaries. Chem. Engng Sci. 192, 218–234.CrossRefGoogle Scholar
Bashtani, F., Irani, M. & Kantzas, A. 2021 Scale up of pore-network models into reservoir scale: optimization of inflow control devices placement. SPE J. 1-18, SPE-208601-PA.Google Scholar
Bijeljic, B., Markicevic, B. & Navaz, H.K. 2011 Capillary climb dynamics in the limits of prevailing capillary and gravity force. Phys. Rev. E 83, 056310.CrossRefGoogle ScholarPubMed
Budaraju, A., Phirani, J., Kondaraju, S. & Bahga, S.S. 2016 Capillary Displacement of Viscous Liquids in Geometries with Axial Variations. Langmuir 32 (41), 10513–10521.CrossRefGoogle ScholarPubMed
Bultreys, T., Van Hoorebeke, L. & Cnudde, V. 2015 Multi-scale, micro-computed tomography-based pore network models to simulate drainage in heterogeneous rocks. Adv. Water Resour. 78, 36–49.CrossRefGoogle Scholar
Clift, R., Grace, J.R. & Weber, M.E. 2005 Bubbles, Drops, and Particles, 1st edn. Dover.Google Scholar
Das, D.B. & Hassanizadeh, S.M. 2010 Upscaling Multiphase Flow in Porous Media: From Pore to Core and Beyond. Springer.Google Scholar
Das, S., Chanda, S., Eijkel, J.C.T., Tas, N.R., Chakraborty, S. & Mitra, S.K. 2014 Filling of charged cylindrical capillaries. Phys. Rev. E 90, 043011.CrossRefGoogle ScholarPubMed
Das, S., Guha, A. & Mitra, S.K. 2013 Exploring new scaling regimes for streaming potential and electroviscous effects in a nanocapillary with overlapping electric double layers. Anal. Chim. Acta 804, 159–166.CrossRefGoogle Scholar
Das, S. & Mitra, S.K. 2013 Different regimes in vertical capillary filling. Phys. Rev. E 87 (6), 063005.CrossRefGoogle ScholarPubMed
Das, S., Waghmare, P.R. & Mitra, S.K. 2012 Early regimes of capillary filling. Phys. Rev. E 86 (6), 067301.CrossRefGoogle ScholarPubMed
de Boer, R. 2006 Trends in Continuum Mechanics of Porous Media. Springer.Google Scholar
de Gennes, P., Brochard-Wyart, F. & Quere, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.CrossRefGoogle Scholar
Dereyssat, M., Courbin, L., Reyssat, E. & Stone, H. 2008 Imbibition in geometries with axial variations. J. Fluid Mech. 615, 335–344.CrossRefGoogle Scholar
Echakouri, M., Salama, A. & Henni, A. 2020 Experimental and computational fluid dynamics investigation of the deterioration of the rejection capacity of the membranes used in the filtration of oily water systems. ACS ES&T Water 1 (3), 728–744.CrossRefGoogle Scholar
El Amin, M., Salama, A. & Sun, S. 2011 Solute transport with chemical reaction in single and multi-phase flow in porous media. In Mass Transfer in Multiphase Systems and its Applications (ed. El-Amin, M.). IntechOpen. doi:10.5772/594.CrossRefGoogle Scholar
Elizalde, E., Urteaga, R., Koropecki, R.R. & Berli, C.L.A. 2014 Inverse problem of capillary filling. Phys. Rev. Lett. 112, 134502.CrossRefGoogle ScholarPubMed
Erickson, D., Li, D. & Park, C.B. 2002 Numerical simulations of capillary-driven flows in nonuniform cross-sectional capillaries. J. Colloid Interface Sci. 250, 422–430.CrossRefGoogle ScholarPubMed
Fries, N. & Dreyer, M. 2008 The transition from inertial to viscous flow in capillary rise. J. Colloid. Interface Sci. 327, 125–128.CrossRefGoogle ScholarPubMed
Golparvar, A., Zhou, Y., Wu, K., Ma, J. & Yu, Z. 2018 A comprehensive review of pore scale modeling methodologies for multiphase flow in porous media. Adv. Geo-Energy Res. 2 (4), 418–440.CrossRefGoogle Scholar
Gorce, J.-B., Hewitt, I. & Vella, D. 2016 Capillary imbibition into converging tubes: beating Washburn's law and the optimal imbibition of liquids. Langmuir 32 (6), 1560–1567.CrossRefGoogle ScholarPubMed
Gueto-Felgueroso, L., Fu, X. & Juanes, R. 2018 Pore-scale modeling of phase change in porous media. Phys. Rev. Fluids 3, 084302.CrossRefGoogle Scholar
Guo, Y., Zhang, L., Sun, H., Yang, Y., Xu, Z., Bao, B. & Yao, J. 2021 The simulation of liquid flow in the pore network model of nanoporous media. ASME. J. Energy Resour. Technol. 143 (3), 033006.CrossRefGoogle Scholar
Hammecker, C., Mertz, J.-D., Fischer, C. & Jeannette, D. 1993 A geometrical model for numerical simulation of capillary imbibition in sedimentary rocks. Transp. Porous Media 12, 125–141.CrossRefGoogle Scholar
Hultmark, M., Aristoff, J.M. & Stone, H.A.J. 2011 The influence of the gas phase on liquid imbibition in capillary tubes. Fluid Mech 678, 600–606.CrossRefGoogle Scholar
Joekar-Niasar, V., Prodanovic, M., Wildenschild, D. & Hassanezadeh, S.M. 2010 Network model investigation of interfacial area, capillary pressure and saturation relationships in granular porous media. Water Resour. Res. 46, W06526.CrossRefGoogle Scholar
Kornev, K.G. & Neimark, A.V. 2011 Spontaneous penetration of liquids into capillaries and porous membranes revisited. J. Colloid. Interface Sci. 235 (1), 101–113.CrossRefGoogle Scholar
Liou, W.W., Peng, P. & Parker, P.E. 2009 Analytical modeling of capillary flow in tubes of nonuniform cross section. J. Coll. Interface Sci. 333 (1), 389–399.CrossRefGoogle ScholarPubMed
Lucas, R. 1918 Rate of capillary ascension of liquids. Kolloidn. Z. 23 (15), 15–22.CrossRefGoogle Scholar
Maggi, F. & Alonso-Marroquin, F. 2012 Multiphase capillary flows. Intl J. Multiphase Flow 42, 62–73.CrossRefGoogle Scholar
Ovaysi, S. & Piri, M. 2011 Pore-scale modeling of dispersion in disordered porous media. J. Contam. Hydrol. 124 (1–4), 68–81.CrossRefGoogle ScholarPubMed
Raeini, A.Q., Blunt, M.J. & Bijeljic, B. 2012 Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 231 (17), 5653–5668.CrossRefGoogle Scholar
Ramakrishnan, S., Wu, P., Zhang, H. & Wasan, D.T. 2019 Dynamics in closed and open capillaries. J. Fluid Mech. 872, 5–38.CrossRefGoogle Scholar
Reyssat, E. 2014 Drops and bubbles in wedges. J. Fluid Mech. 748, 641–662.CrossRefGoogle Scholar
Salama, A. 2021 a Imbibition and drainage processes in capillaries: a generalized model, effect of inertia, and a numerical algorithm. Phys. Fluids 33 (8), 082104.CrossRefGoogle Scholar
Salama, A. 2021 b A generalized analytical model for estimating the rate of imbibition/drainage of wetting/nonwetting fluids in capillaries. Chem. Engng Sci. 243, 116788.CrossRefGoogle Scholar
Salama, A., Cai, J., Kou, J., Sun, S., El Amin, M.F. & Wang, Y. 2021 Investigation of the dynamics of immiscible displacement of a ganglion in capillaries. Capillarity 4 (2), 31–44.CrossRefGoogle Scholar
Salama, A., Kou, J., Alyan, A. & Husein, M.M. 2022 Capillary-driven ejection of a droplet from a micropore into a channel: a theoretical model and a computational fluid dynamics verification. Langmuir 38 (14), 4461–4472.CrossRefGoogle Scholar
Salama, A. & Van Geel, P.J. 2008 flow and solute transport in saturated porous media I: the continuum hypothesis. Porous Media 11 (4), 403–413.CrossRefGoogle Scholar
Salama, A., Zoubeik, M. & Henni, A. 2017 A multicontinuum approach for the problem of filtration of oily water systems across thin flat membranes: I. The framework. AIChE J. 63 (10), 4604–4615.CrossRefGoogle Scholar
Taroni, M. & Vella, D. 2012 Multiple equilibria in a simple elastocapillary system. J. Fluid Mech. 712, 273–294.CrossRefGoogle Scholar
Waghmare, R. & Mittra, S.K. 2010 Finite reservoir effect on capillary flow of microbead suspension in rectangular microchannels. J. Colloid. Interface Sci. 351 (2), 561–569.CrossRefGoogle ScholarPubMed
Walls, P.L.L., Deqidt, G. & Bird, J.C. 2016 Capillary displacement of viscous liquids. Langmuir 32 (13), 3186–3190.CrossRefGoogle ScholarPubMed
Wang, Z., Chang, C.-C., Hong, S.-J., Sheng, Y.-J. & Tsao, H.-K. 2012 Capillary rise in a microchannel of arbitrary shape and wettability: hysteresis loop. Langmuir 28 (49), 16917–16926.CrossRefGoogle Scholar
Washburn, E.W. 1921 The dynamics of capillary flow. Phys. Rev. 17 (3), 273.CrossRefGoogle Scholar
Whittaker, S. 1999 The Method of Volume Averaging. Springer.CrossRefGoogle Scholar
Xiao, Y., Yang, F. & Pitchumani, R. 2006 A generalized analysis of capillary flows in channels. J. Colloid. Interface Sci. 298 (2), 880–888.CrossRefGoogle ScholarPubMed
Young, W.B. 2004 Analysis of capillary flows in non-uniform cross-sectional capillaries. Colloids Surf. A 234, 123–128.CrossRefGoogle Scholar
Zoubeik, M., Salama, A. & Henni, A. 2018 A novel antifouling technique for the crossflow filtration using porous membranes: Experimental and CFD investigations of the periodic feed pressure technique. Water Res. 146, 159–176.CrossRefGoogle ScholarPubMed