Published online by Cambridge University Press: 28 April 2022
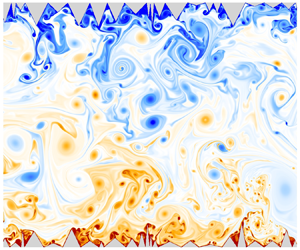
We present a two-dimensional numerical study of turbulent Rayleigh–Bénard convection with air as the working fluid over a multi-scale randomly roughened surface in a rectangular box of aspect ratio 2 over three decades of Rayleigh number ( $10^8 \leq {\textit {Ra}} \leq 10^{11}$). With varied response of the roughness elements at different
$10^8 \leq {\textit {Ra}} \leq 10^{11}$). With varied response of the roughness elements at different  ${\textit {Ra}}$, enhanced heat transfer scaling (
${\textit {Ra}}$, enhanced heat transfer scaling ( $\gamma =0.41$) is retained throughout the explored
$\gamma =0.41$) is retained throughout the explored  ${\textit {Ra}}$ range. The plume emission process is triggered from the taller roughness elements at a lower
${\textit {Ra}}$ range. The plume emission process is triggered from the taller roughness elements at a lower  ${\textit {Ra}}$, while smaller elements contribute significantly at higher
${\textit {Ra}}$, while smaller elements contribute significantly at higher  ${\textit {Ra}}$. Increased plume emission frequency compared to the smooth case is reflected from the enhanced volume fraction and thermal dissipation rate of plumes. The tip of the roughness elements exhibits the highest temperature and vertical velocity fluctuations, while washing out of the trapped fluid in the throat region holds the key to enhanced heat flux at higher
${\textit {Ra}}$. Increased plume emission frequency compared to the smooth case is reflected from the enhanced volume fraction and thermal dissipation rate of plumes. The tip of the roughness elements exhibits the highest temperature and vertical velocity fluctuations, while washing out of the trapped fluid in the throat region holds the key to enhanced heat flux at higher  ${\textit {Ra}}$. Increased localized pockets of fluid at higher
${\textit {Ra}}$. Increased localized pockets of fluid at higher  ${\textit {Ra}}$ indicate better inter-scale energy transfer, which is reflected in higher energy content at all scales in the computed temperature spectra. The decomposition of the flow field into orthogonal modes reveals that heat transfer enhancement at higher
${\textit {Ra}}$ indicate better inter-scale energy transfer, which is reflected in higher energy content at all scales in the computed temperature spectra. The decomposition of the flow field into orthogonal modes reveals that heat transfer enhancement at higher  ${\textit {Ra}}$ is associated with multiple small-scale structures. Owing to better energy transfer and intense localized fluctuations, modal distribution of energy is less severe for higher
${\textit {Ra}}$ is associated with multiple small-scale structures. Owing to better energy transfer and intense localized fluctuations, modal distribution of energy is less severe for higher  ${\textit {Ra}}$, and stable twin large-scale rolls do not favour an efficient heat transport process.
${\textit {Ra}}$, and stable twin large-scale rolls do not favour an efficient heat transport process.