Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T04:04:39.992Z Has data issue: false hasContentIssue false
  • English
  • Français

The internal gravity wave field emitted by a stably stratified turbulent wake

Published online by Cambridge University Press:  27 February 2013

Ammar M. Abdilghanie  and
Peter J. Diamessis
Ammar M. Abdilghanie
Affiliation:
Leadership Computing Facility, Argonne National Laboratory, Argonne, IL 60439, USA
Peter J. Diamessis*
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

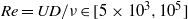The internal gravity wave (IGW) field emitted by a stably stratified, initially turbulent, wake of a towed sphere in a linearly stratified fluid is studied using fully nonlinear numerical simulations. A wide range of Reynolds numbers, $\mathit{Re}= UD/ \nu \in [5\times 1{0}^{3} , 1{0}^{5} ] $ and internal Froude numbers, 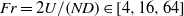$\mathit{Fr}= 2U/ (ND)\in [4, 16, 64] $ (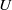$U$, 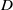$D$ are characteristic body velocity and length scales, and 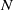$N$ is the buoyancy frequency) is examined. At the higher 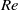$\mathit{Re}$ examined, secondary Kelvin–Helmholtz instabilities and the resulting turbulent events, directly linked to a prolonged non-equilibrium (NEQ) regime in wake evolution, are responsible for IGW emission that persists up to 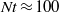$Nt\approx 100$. In contrast, IGW emission at the lower 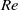$\mathit{Re}$ investigated does not continue beyond 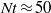$Nt\approx 50$ for the three $\mathit{Fr}$ values considered. The horizontal wavelengths of the most energetic IGWs, obtained by continuous wavelet transforms, increase with 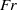$\mathit{Fr}$ and appear to be smaller at the higher 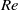$\mathit{Re}$, especially at late times. The initial value of these wavelengths is set by the wake height at the beginning of the NEQ regime. At the lower 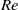$\mathit{Re}$, consistent with a recently proposed model, the waves propagate over a narrow range of angles that minimize viscous decay along their path. At the higher 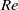$\mathit{Re}$, wave motion is much less affected by viscosity, at least initially, and early-time wave propagation angles extend over a broader range of values which are linked to increased efficiency in momentum extraction from the turbulent wake source.

JFM classification

Geophysical and Geological Flows: Stratified flows Wakes/Jets: Wakes/Jets Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 104 - 139
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdilghanie, A. M. 2010 A numerical investigation of turbulence-driven and forced generation of internal gravity waves in stratified mid-water. PhD thesis, Cornell University.Google Scholar
Addison, P. S. 2002 The Illustrated Wavelet Transform Handbook. Institute of Physics.CrossRefGoogle Scholar
Aguilar, D. A. & Sutherland, B. R. 2006 Internal wave generation from rough topography. Phys. Fluids 18, 066603.CrossRefGoogle Scholar
Aguilar, D. A., Sutherland, B. R. & Muraki, D. J. 2006 Laboratory generation of internal waves from sinusoidal topography. Deep-Sea Res. II 53 (1–2), 96–115.Google Scholar
Bonneton, P., Chomaz, J. M. & Hopfinger, E. J. 1993 Internal waves produced by the turbulent wake of a sphere moving horizontally in a stratified fluid. J. Fluid Mech. 254, 23–40.CrossRefGoogle Scholar
Bonnier, M., Bonneton, P. & Eiff, O. 1998 Far-wake of a sphere in a stably stratified fluid: characterization of vortex structures. Appl. Sci. Res. 59, 269–281.CrossRefGoogle Scholar
Bowman, A. W. & Azzalini, A. 1997 Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-Plus Illustrations, Oxford Statistical Science Series, vol. 18. Oxford University Press.CrossRefGoogle Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J. M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.CrossRefGoogle Scholar
Broutman, D., Rottman, J. W. & Eckert, S. D. 2004 Ray methods for internal waves in the atmosphere and ocean. Annu. Rev. Fluid Mech. 36, 233–253.CrossRefGoogle Scholar
Brucker, K. A. & Sarkar, S. 2010 A study of momentumless wakes in stratified fluids. J. Fluid Mech. 652, 373–404.CrossRefGoogle Scholar
Chashechkin, Y. D. 1989 Hydrodynamics of a sphere in a stratified fluid. Fluid Dyn. 24 (1), 1–7.CrossRefGoogle Scholar
Clarke, H. A. & Sutherland, B. R 2010 Generation, propagation, and breaking of an internal wave beam. Phys. Fluids 22, 076601.CrossRefGoogle Scholar
Dallard, T. & Spedding, G. R. 1993 2-D wavelet transforms: generalisation of the Hardy space and application to experimental studies. Eur. J. Mech. (B/Fluids) 12 (1), 107–134.Google Scholar
Deloncle, A., Billant, P. & Chomaz, J. M. 2008 Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation. J. Fluid Mech. 599, 229–239.CrossRefGoogle Scholar
Diamessis, P. J. 2010 Vertical transport in high Reynolds numbers stratified turbulent wakes. In Sixth International Symposium on Environmental Hydraulics, Athens, Greece.Google Scholar
Diamessis, P. J., Domaradzki, J. A. & Hesthaven, J. S. 2005 A spectral multidomain penalty method model for the simulation of high Reynolds number localized stratified turbulence. J. Comput. Phys. 202, 298–322.CrossRefGoogle Scholar
Diamessis, P. J., Gurka, R. & Liberzon, A. 2010 Spatial characterization of vortical structures and internal waves in a stratified turbulent wake using proper orthogonal decomposition. Phys. Fluids 22, 086601.CrossRefGoogle Scholar
Diamessis, P. J. & Nomura, K. K. 2000 Interaction of vorticity, rate-of-strain and scalar gradient in stratified homogeneous sheared turbulence. Phys. Fluids 12, 1166–1188.CrossRefGoogle Scholar
Diamessis, P. J., Spedding, G. R. & Domaradzki, A. J. 2011 Similarity scaling and vorticity structure in high Reynolds number stably stratified turbulent wakes. J. Fluid Mech. 671, 52–95.CrossRefGoogle Scholar
Dohan, K. & Sutherland, B. R. 2003 Internal waves generated from a turbulent mixed region. Phys. Fluids 15, 488.CrossRefGoogle Scholar
Dohan, K. & Sutherland, B. R. 2005 Numerical and laboratory generation of internal waves from turbulence. Dyn. Atmos. Oceans 40, 43–56.CrossRefGoogle Scholar
Dommermuth, D. G., Rottman, J. W., Innis, G. E. & Novikov, E. A. 2002 Numerical simulation of the wake of a towed sphere in a weakly stratified fluid. J. Fluid Mech. 473, 83–101.CrossRefGoogle Scholar
Dougherty, J. P. 1961 The anisotropy of turbulence at the meteor level. J. Atmos. Terr. Phys. 21 (2–3), 210–213.CrossRefGoogle Scholar
Druzhinin, O. A. 2009 Generation of internal waves by a turbulent jet in a stratified fluid. Fluid Dyn. 44, 213–223.CrossRefGoogle Scholar
Durran, D. R. 1999 Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. Springer.CrossRefGoogle Scholar
Gayen, B., Taylor, R. J. & Sarkar, S. 2010 Large eddy simulation of a stratified boundary layer under an oscillatory current. J. Fluid Mech. 643, 233–266.CrossRefGoogle Scholar
Gibson, C. H. 1980 Fossil temperature, salinity and vorticity in the ocean. In Marine Turbulence (ed. Nihoul, J. C. T.), pp. 221–258. Elsevier.Google Scholar
Gilreath, H. E. & Brandt, A. 1985 Experiments on the generation of internal waves in a stratified fluid. AIAA J. 23, 693–700.CrossRefGoogle Scholar
Gourlay, M. J., Arendt, S. C., Fritts, D. C. & Werne, J. 2001 Numerical modelling of initially turbulent wakes with net momentum. Phys. Fluids 13, 3783–3802.CrossRefGoogle Scholar
Hopfinger, E. J., Flor, J. B., Chomaz, J. M. & Bonneton, P. 1991 Internal waves generated by a moving sphere and its wake in a stratified fluid. Exp. Fluids 11 (4), 255–261.CrossRefGoogle Scholar
Israeli, M. & Orszag, S. A. 1981 Approximation of radiation boundary conditions. J. Comput. Phys. 41 (1), 115–135.CrossRefGoogle Scholar
Itsweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H. 1993 Turbulence in stratified shear flows: implications for interpreting shear-induced mixing in the ocean. J. Phys. Oceanogr. 23, 1508–1522.2.0.CO;2>CrossRefGoogle Scholar
Keeler, R. N., Bondur, V. G. & Gibson, C. H. 2005 Optical satellite imagery detection of internal wave effects from a submerged turbulent outfall in the stratified ocean. Geophys. Res. Lett. 32 (12), L12610.CrossRefGoogle Scholar
Klemp, J. B. & Lilly, D. K. 1978 Numerical simulation of hydrostatic mountain waves. J. Atmos. Sci. 35 (1), 78–107.2.0.CO;2>CrossRefGoogle Scholar
Lighthill, J. 1978 Waves in Fluids. Cambridge University Press.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically. I. General theory. Proc. R. Soc. Lond. A 211 (1107), 564–587.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.2.0.CO;2>CrossRefGoogle Scholar
Linborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.CrossRefGoogle Scholar
Linden, P. F. 1975 The deepening of a mixed layer in a stratified fluid. J. Fluid Mech. 71 (2), 385–405.CrossRefGoogle Scholar
Meng, J. C. S. & Rottman, J. W. 1988 Linear internal waves generated by density and velocity perturbations in a linearly stratified fluid. J. Fluid Mech. 186, 419–444.CrossRefGoogle Scholar
Meunier, P., Diamessis, P. J. & Spedding, G. R. 2006 Self-preservation of stratified momentum wakes. Phys. Fluids 18, 106601.CrossRefGoogle Scholar
Miles, J. W. 1971 Internal waves generated by a horizontally moving source. J. Geophys. Astrophys. Fluid Dyn. 2 (1), 63–87.CrossRefGoogle Scholar
Moum, J. N., Hebert, D., Paulson, C. A. & Caldwell, D. R. 1992 Turbulence and internal waves at the equator. Part I: Statistics from towed thermistors and a microstructure profiler. J. Phys. Oceanogr. 22 (11), 1330–1345.2.0.CO;2>CrossRefGoogle Scholar
Munroe, J. R. & Sutherland, B. R. 2008 Generation of internal waves by sheared turbulence: experiments. Environ. Fluid Mech. 8 (5), 527–534.CrossRefGoogle Scholar
Nappo, C. J. 2002 An Introduction to Atmospheric Gravity Waves. Academic.Google Scholar
Orszag, S. A. & Pao, Y. H. 1975 Numerical computation of turbulent shear flows. Adv. Geophys. 18 (1), 225–236.CrossRefGoogle Scholar
Ozmidov, R. V. 1965 On the turbulent exchange in a stably stratified ocean. Izv. Acad. Sci. USSR, Atmos. Ocean. Phys. 1, 853–860.Google Scholar
Pao, H. P., Lai, R. Y. & Schemm, C. E. 1982 Vortex trails in stratified fluids. Tech. Rep. 3(1). Johns Hopkins Applied Physics Laboratory Technical Digest.Google Scholar
Peat, K. S. & Stevenson, T. N. 1975 Internal waves around a body moving in a compressible density-stratified fluid. J. Fluid Mech. 70 (4), 673–688.CrossRefGoogle Scholar
Pham, H. T., Sarkar, S. & Brucker, K. A. 2009 Dynamics of a stratified shear layer above a region of uniform stratification. J. Fluid Mech. 630, 191–223.CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2002 Internal gravity wave emission from a pancake vortex: an example of wave–vortex interaction in strongly stratified flows. Phys. Fluids 14, 1259.CrossRefGoogle Scholar
Riley, J. J. & de Bruyn Kops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. Phys. Fluids 15, 2047–2059.CrossRefGoogle Scholar
Riley, J. J. & Lindborg, E. 2008 Stratified turbulence: a possible interpretation of some geophysical turbulence measurements. J. Atmos. Sci. 65 (7), 2416–2424.CrossRefGoogle Scholar
Riley, J. J. & Metcalfe, R. W. 1987 Direct numerical simulations of turbulent patches in stably-stratified fluids. In Stratified Flows I. Proceedings 3rd International Symp. on Stratified Flows, California Institute of Technology, Pasadena.Google Scholar
Riley, J. J., Metcalf, R. W. & Weissman, M. A. 1981 Direct numerical simulations of turbulence in homogeneously stratified fluids. In Non-linear Properties of Internal Waves, pp. 79–112. AIP.Google Scholar
Robey, H. F. 1997 The generation of internal waves by a towed sphere and its wake in a thermocline. Phys. Fluids 9, 3353.CrossRefGoogle Scholar
Smyth, W. D. 1999 Dissipation-range geometry and scalar spectra in sheared stratified turbulence. J. Fluid Mech. 401, 209–242.CrossRefGoogle Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12, 1327.CrossRefGoogle Scholar
Spedding, G. R. 1997 The evolution of initially turbulent bluff-body wakes at high internal Froude number. J. Fluid Mech. 337, 283–301.CrossRefGoogle Scholar
Spedding, G. R. 2002 Vertical structure in stratified wakes with high initial Froude number. J. Fluid Mech. 454, 71–112.CrossRefGoogle Scholar
Spedding, G. R., Browand, F. K., Bell, R. & Chen, J. 2000 Internal waves from intermediate, or late-wake vortices. In Stratified Flows I – Fifth International Symposium (ed. R. Pieters, N. Yonemitsu & G.A. Lawrence), vol. 1, pp. 113–118. University of British Columbia, Vancouver.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.CrossRefGoogle Scholar
Spedding, G. R., Browand, F. K., Huang, N. E. & Long, S. R. 1993 A 2-D complex wavelet analysis of an unsteady wind-generated surface wave field. Dyn. Atmos. Oceans 20 (1–2), 55–77.CrossRefGoogle Scholar
de Statler, M. B., Sarkar, S. & Brucker, K. A. 2010 Effect of the Prandtl number on a stratified turbulent wake. Phys. Fluids 22, 095102.CrossRefGoogle Scholar
Sutherland, B. R. 2001 Finite-amplitude internal wavepacket dispersion and breaking. J. Fluid Mech. 429, 343–380.CrossRefGoogle Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.CrossRefGoogle Scholar
Sutherland, B. R., Flynn, M. R. & Dohan, K. 2004 Internal wave excitation from a collapsing mixed region. Deep-Sea Res. II 51, 2889–2904.Google Scholar
Sutherland, B. R. & Linden, P. F. 1998 Internal wave excitation from stratified flow over a thin barrier. J. Fluid Mech. 377, 223–252.CrossRefGoogle Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.CrossRefGoogle Scholar
Taylor, J. R. & Sarkar, S. 2008 Stratification effects in a bottom Ekman layer. J. Phys. Oceanogr. 38 (11), 2535–2555.CrossRefGoogle Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.CrossRefGoogle Scholar
Townsend, A. A. 1965 Excitation of internal waves by a turbulent boundary layer. J. Fluid Mech. 22 (2), 241–252.CrossRefGoogle Scholar
Townsend, A. A. 1968 Excitation of internal waves in a stably-stratified atmosphere with considerable wind-shear. J. Fluid Mech. 32 (1), 145–171.CrossRefGoogle Scholar
Trauth, M. H. 2010 MATLAB® Recipes for Earth Sciences. Springer.CrossRefGoogle Scholar
Voisin, B. 1991 Internal wave generation in uniformly stratified fluids. Part 1. Green’s function and point sources. J. Fluid Mech. 231, 439–480.CrossRefGoogle Scholar
Voisin, B. 1994 Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources. J. Fluid Mech. 261, 333–374.CrossRefGoogle Scholar
Wijesekera, H. W. & Dillon, T. M. 1991 Internal waves and mixing in the upper equatorial Pacific Ocean. J. Geophys. Res. 96 (C4), 7115–7125.CrossRefGoogle Scholar
Wu, J. 1969 Mixed region collapse with internal wave generation in a density-stratified medium. J. Fluid Mech. 35 (3), 531–544.CrossRefGoogle Scholar
Zavol’Skii, N. A. & Zaitsev, A. A. 1984 Development of internal waves generated by a concentrated pulse source in an infinite uniformly stratified fluid. J. Appl. Mech. Tech. Phys. 25 (6), 862–867.CrossRefGoogle Scholar