Article contents
Intermittent dynamics of turbulence hibernation in Newtonian and viscoelastic minimal channel flows
Published online by Cambridge University Press: 17 January 2012
Abstract
Maximum drag reduction (MDR), the asymptotic upper limit of reduction in turbulent friction drag by polymer additives, is the most important unsolved problem in viscoelastic turbulence. Recent studies of turbulence in minimal flow units have identified time intervals showing key features of MDR. These intervals, denoted ‘hibernating turbulence’ are found in both Newtonian and viscoelastic flows. The present study provides a comprehensive examination of this turbulence hibernation phenomenon in the minimal channel geometry, and discusses its impact on the turbulent dynamics and drag reduction. Similarities between hibernating turbulence and MDR are established in terms of both flow statistics (an intermittency factor, mean and fluctuating components of velocity) and flow structure (weak vortices and nearly streamwise-invariant kinematics). Hibernation occurs more frequently at high levels of viscoelasticity, leading to flows that increasingly resemble MDR. Viscoelasticity facilitates the occurrence of hibernation by suppressing the conventional ‘active’ turbulence, but has little influence on hibernation itself. At low Weissenberg number 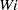 , the average duration of active turbulence intervals is constant, but above a critical value of
, the average duration of active turbulence intervals is constant, but above a critical value of 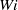 , the duration decreases dramatically, and accordingly, the fraction of time spent in hibernation increases. This observation can be explained with a simple mathematical model that posits that the lifetime of an active turbulence interval is the time that it takes for the turbulence to stretch polymer molecules to a certain threshold value; once the molecules exceed this threshold, they exert a large enough stress on the flow to suppress the active turbulence. This model predicts an explicit form for the duration as a function of
, the duration decreases dramatically, and accordingly, the fraction of time spent in hibernation increases. This observation can be explained with a simple mathematical model that posits that the lifetime of an active turbulence interval is the time that it takes for the turbulence to stretch polymer molecules to a certain threshold value; once the molecules exceed this threshold, they exert a large enough stress on the flow to suppress the active turbulence. This model predicts an explicit form for the duration as a function of 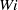 and the simulation results match this prediction very closely. The critical point where hibernation frequency becomes substantially increased coincides with the point where qualitative changes are observed in overall flow statistics – the transition between ‘low-drag-reduction’ and ‘high-drag-reduction’ regimes. Probability density functions of important variables reveal a much higher level of intermittency in the turbulent dynamics after this transition. It is further confirmed that hibernating turbulence is a Newtonian structure during which polymer extension is small. Based on these results, a framework is proposed that explains key transitions in viscoelastic turbulence, especially the convergence toward MDR.
and the simulation results match this prediction very closely. The critical point where hibernation frequency becomes substantially increased coincides with the point where qualitative changes are observed in overall flow statistics – the transition between ‘low-drag-reduction’ and ‘high-drag-reduction’ regimes. Probability density functions of important variables reveal a much higher level of intermittency in the turbulent dynamics after this transition. It is further confirmed that hibernating turbulence is a Newtonian structure during which polymer extension is small. Based on these results, a framework is proposed that explains key transitions in viscoelastic turbulence, especially the convergence toward MDR.
JFM classification
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 46
- Cited by


