Article contents
Intermittency in the relative separations of tracers and of heavy particles in turbulent flows
Published online by Cambridge University Press: 23 September 2014
Abstract
Results from direct numerical simulations (DNS) of particle relative dispersion in three-dimensional homogeneous and isotropic turbulence at Reynolds number 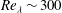 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{Re}}_{\lambda } \sim 300$ are presented. We study point-like passive tracers and heavy particles, at Stokes number
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\mathit{Re}}_{\lambda } \sim 300$ are presented. We study point-like passive tracers and heavy particles, at Stokes number 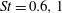 $\mathit{St}=0.6,1$ and 5. Particles are emitted from localised sources, in bunches of thousands, periodically in time, allowing an unprecedented statistical accuracy to be reached, with a total number of events for two-point observables of the order of
$\mathit{St}=0.6,1$ and 5. Particles are emitted from localised sources, in bunches of thousands, periodically in time, allowing an unprecedented statistical accuracy to be reached, with a total number of events for two-point observables of the order of 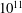 ${10^{11}}$. The right tail of the probability density function (PDF) for tracers develops a clear deviation from Richardson’s self-similar prediction, pointing to the intermittent nature of the dispersion process. In our numerical experiment, such deviations are manifest once the probability to measure an event becomes of the order of – or rarer than – one part over one million, hence the crucial importance of a large dataset. The role of finite-Reynolds-number effects and the related fluctuations when pair separations cross the boundary between viscous and inertial range scales are discussed. An asymptotic prediction based on the multifractal theory for inertial range intermittency and valid for large Reynolds numbers is found to agree with the data better than the Richardson theory. The agreement is improved when considering heavy particles, whose inertia filters out viscous scale fluctuations. By using the exit-time statistics we also show that events associated with pairs experiencing unusually slow inertial range separations have a non-self-similar PDF.
${10^{11}}$. The right tail of the probability density function (PDF) for tracers develops a clear deviation from Richardson’s self-similar prediction, pointing to the intermittent nature of the dispersion process. In our numerical experiment, such deviations are manifest once the probability to measure an event becomes of the order of – or rarer than – one part over one million, hence the crucial importance of a large dataset. The role of finite-Reynolds-number effects and the related fluctuations when pair separations cross the boundary between viscous and inertial range scales are discussed. An asymptotic prediction based on the multifractal theory for inertial range intermittency and valid for large Reynolds numbers is found to agree with the data better than the Richardson theory. The agreement is improved when considering heavy particles, whose inertia filters out viscous scale fluctuations. By using the exit-time statistics we also show that events associated with pairs experiencing unusually slow inertial range separations have a non-self-similar PDF.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 21
- Cited by


