Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-20T13:18:46.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Interfacial instability in a viscoelastic microfluidic coflow system

Published online by Cambridge University Press:  04 December 2024

S. Hazra Open the ORCID record for S. Hazra [Opens in a new window] ,
L. Malik Open the ORCID record for L. Malik [Opens in a new window] ,
T. Sujith Open the ORCID record for T. Sujith [Opens in a new window]  and
A.K. Sen Open the ORCID record for A.K. Sen [Opens in a new window]
S. Hazra
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
L. Malik
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
T. Sujith
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
A.K. Sen*
Affiliation:
Micro Nano Bio Fluidics Unit, Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

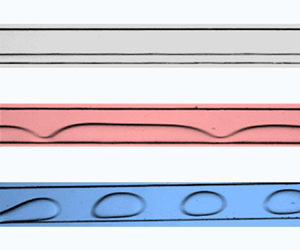
Understanding interfacial instability in a coflow system has relevance in the effective manipulation of small objects in microfluidic applications. We experimentally elucidate interfacial instability in stratified coflow systems of Newtonian and viscoelastic fluid streams in microfluidic confinements. By performing a linear stability analysis, we derive equations that describe the complex wave speed and the dispersion relationship between wavenumber and angular frequency, thus categorizing the behaviour of the systems into two main regimes: stable (with a flat interface) and unstable (with either a wavy interface or droplet formation). We characterize the regimes in terms of the capillary numbers of the phases in a comprehensive regime plot. We decipher the dependence of interfacial instability on fluidic parameters by decoupling the physics into viscous and elastic components. Remarkably, our findings reveal that elastic stratification can both stabilize and destabilize the flow, depending on the fluid and flow parameters. We also examine droplet formation, which is important for microfluidic applications. Our findings suggest that adjusting the viscous and elastic properties of the fluids can control the transition between wavy and droplet-forming unstable regimes. Our investigation uncovers the physics behind the instability involved in interfacial flows of Newtonian and viscoelastic fluids in general, and the unexplored behaviour of interfacial waves in stratified liquid systems. The present study can lead to a better understanding of the manipulation of small objects and production of droplets in microfluidic coflow systems.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Instability: Instability Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1000 , 10 December 2024 , A96
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

These authors contributed equally to this work.

References

Ambravaneswaran, B., Subramani, H.J., Phillips, S.D. & Basaran, O.A. 2004 Dripping-jetting transitions in a dripping faucet. Phys. Rev. Lett. 93 (3), 034501.CrossRefGoogle Scholar
Anna, S.L. 2016 Droplets and bubbles in microfluidic devices. Annu. Rev. Fluid Mech. 48 (1), 285–309.CrossRefGoogle Scholar
Azaiez, J. & Homsy, G.M. 1994 Linear stability of free shear flow of viscoelastic liquids. J. Fluid Mech. 268, 37–69.CrossRefGoogle Scholar
Barnea, D. & Taitel, Y. 1993 Kelvin–Helmholtz stability criteria for stratified flow: viscous versus non-viscous (inviscid) approaches. Intl J. Multiphase Flow 19 (4), 639–649.CrossRefGoogle Scholar
Boomkamp, P.A.M. & Miesen, R.H.M. 1996 Classification of instabilities in parallel two-phase flow. Intl J. Multiphase Flow 22, 67–88.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover Publications.Google Scholar
Charles, M.E. & Lilleleht, L.U. 1965 An experimental investigation of stability and interfacial waves in co-current flow of two liquids. J. Fluid Mech. 22 (2), 217–224.CrossRefGoogle Scholar
Charru, F. & Hinch, E.J. 2000 ‘Phase diagram’ of interfacial instabilities in a two-layer Couette flow and mechanism of the long-wave instability. J. Fluid Mech. 414, 195–223.CrossRefGoogle Scholar
Chekila, A., Nouar, C., Plaut, E. & Nemdili, A. 2011 Subcritical bifurcation of shear-thinning plane poiseuille flows. J. Fluid Mech. 686, 272–298.CrossRefGoogle Scholar
Deng, N.-N., Wang, W., Ju, X.-J., Xie, R. & Chu, L.-Y. 2016 Spontaneous transfer of droplets across microfluidic laminar interfaces. Lab on a Chip 16 (22), 4326–4332.CrossRefGoogle ScholarPubMed
Ebagninin, K.W., Benchabane, A. & Bekkour, K. 2009 Rheological characterization of poly(ethylene oxide) solutions of different molecular weights. J. Colloid Interface Sci. 336 (1), 360–367.CrossRefGoogle ScholarPubMed
Ganpule, H.K. & Khomami, B. 1999 An investigation of interfacial instabilities in the superposed channel flow of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 81 (1–2), 27–69.CrossRefGoogle Scholar
Govindarajan, R. & Sahu, K.C. 2014 Instabilities in viscosity-stratified flow. Annu. Rev. Fluid Mech. 46 (1), 331–353.CrossRefGoogle Scholar
Guerrero, J., Chang, Y.-W., Fragkopoulos, A.A. & Fernandez-Nieves, A. 2019 Capillary-based microfluidics – coflow, flow-focusing, electro-coflow, drops, jets, and instabilities. Small 16 (9), 1904344.CrossRefGoogle ScholarPubMed
Guillot, P., Colin, A., Utada, A.S. & Ajdari, A. 2007 Stability of a jet in confined pressure-driven biphasic flows at low Reynolds numbers. Phys. Rev. Lett. 99 (10), 104502.CrossRefGoogle ScholarPubMed
Hazra, S., Jayaprakash, K.S., Pandian, K., Raj, A., Mitra, S.K. & Sen, A.K. 2019 Non-inertial lift induced migration for label-free sorting of cells in a co-flowing aqueous two-phase system. Analyst 144 (8), 2574–2583.CrossRefGoogle Scholar
Hazra, S., Malik, L., Mitra, S.K. & Sen, A.K. 2022 a Interaction between droplets and co-flow interface in a microchannel: droplet migration and interfacial deformation. Phys. Rev. Fluids 7 (5), 054201.CrossRefGoogle Scholar
Hazra, S., Mitra, S. & Sen, A.K. 2022 b Migration and spreading of droplets across a fluid–fluid interface in microfluidic coflow. Langmuir 38 (31), 9660–9668.CrossRefGoogle ScholarPubMed
Hemachandran, E., Hoque, S.Z., Laurell, T. & Sen, A.K. 2021 Reversible stream drop transition in a microfluidic coflow system via on demand exposure to acoustic standing waves. Phys. Rev. Lett. 127 (13), 134501.CrossRefGoogle Scholar
Hinch, E.J. 1984 A note on the mechanism of the instability at the interface between two shearing fluids. J. Fluid Mech. 144, 463–465.CrossRefGoogle Scholar
Hooper, A.P. 1985 Long-wave instability at the interface between two viscous fluids: thin layer effects. Phys. Fluids 28 (6), 1613.CrossRefGoogle Scholar
Hooper, A.P. & Boyd, W.G.C. 1987 Shear-flow instability due to a wall and a viscosity discontinuity at the interface. J. Fluid Mech. 179, 201–225.CrossRefGoogle Scholar
Hormozi, S., Wielage-Burchard, K. & Frigaard, I.A. 2011 Entry, start up and stability effects in visco-plastically lubricated pipe flows. J. Fluid Mech. 673, 432–467.CrossRefGoogle Scholar
Hu, H.H. & Joseph, D.D. 1989 Lubricated pipelining: stability of core-annular flow. Part 2. J. Fluid Mech. 205, 359.CrossRefGoogle Scholar
Hu, X. & Cubaud, T. 2018 Viscous wave breaking and ligament formation in microfluidic systems. Phys. Rev. Lett. 121 (4), 044502.CrossRefGoogle ScholarPubMed
Hu, X. & Cubaud, T. 2020 From droplets to waves: periodic instability patterns in highly viscous microfluidic flows. J. Fluid Mech. 887, A27.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Jayaprakash, K.S., Banerjee, U. & Sen, A.K. 2016 Dynamics of aqueous droplets at the interface of coflowing immiscible oils in a microchannel. Langmuir 32 (8), 2136–2143.CrossRefGoogle Scholar
Joseph, D.D., Bai, R., Chen, K.P. & Renardy, Y.Y. 1997 Core-annular flows. Annu. Rev. Fluid Mech. 29 (1), 65–90.CrossRefGoogle Scholar
Joseph, P. 1873 Experimental and Theoretical Statics of Liquids Subject to Molecular Forces Only. Gauthier-Villars, Trübner and Co.Google Scholar
Kaneelil, P.R., Pahlavan, A.A., Herrada, M.A., LeRoy, K., Stengel, K., Warner, S., Galea, A.M. & Stone, H.A. 2022 Symmetry breaking of a parallel two-phase flow in a finite length channel. Phys. Rev. Fluids 7 (3), 033904.CrossRefGoogle Scholar
Kao, T.W. & Park, C. 1970 Experimental investigations of the stability of channel flows. Part 1. Flow of a single liquid in a rectangular channel. J. Fluid Mech. 43 (1), 145–164.CrossRefGoogle Scholar
Khomami, B. & Su, K.C. 2000 An experimental/theoretical investigation of interfacial instabilities in superposed pressure-driven channel flow of newtonian and well characterized viscoelastic fluids. J. Non-Newtonian Fluid Mech. 91 (1), 59–84.CrossRefGoogle Scholar
Lashgari, I., Pralits, J.O., Giannetti, F. & Brandt, L. 2012 First instability of the flow of shear-thinning and shear-thickening fluids past a circular cylinder. J. Fluid Mech. 701, 201–227.CrossRefGoogle Scholar
Lee, B.-L. & White, J.L. 1974 An experimental study of rheological properties of polymer melts in laminar shear flow and of interface deformation and its mechanisms in two-phase stratified flow. Trans. Soc. Rheol. 18 (3), 467–492.CrossRefGoogle Scholar
Lewis, D.J. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A Math. Phys. Sci. 202 (1068), 81–96.Google Scholar
Li, C.-H. 1969 Stability of two superposed elasticoviscous liquids in plane Couette flow. Phys. Fluids 12 (3), 531–538.Google Scholar
Renardy, Y. & Joseph, D.D. 1985 Couette flow of two fluids between concentric cylinders. J. Fluid Mech. 150, 381–394.CrossRefGoogle Scholar
Saffman, P.G. & Taylor, G. 1958 The penetration of a fluid into a porous medium or hele-shaw cell containing a more viscous liquid. Proc. R. Soc. Lond. A Math. Phys. Sci. 245 (1242), 312–329.Google Scholar
Sahu, K.C. & Govindarajan, R. 2014 Instability of a free-shear layer in the vicinity of a viscosity-stratified layer. J. Fluid Mech. 752, 626–648.CrossRefGoogle Scholar
Sajeesh, P., Doble, M. & Sen, A.K. 2014 Hydrodynamic resistance and mobility of deformable objects in microfluidic channels. Biomicrofluidics 8 (5), 054112.CrossRefGoogle ScholarPubMed
Su, Y.Y. & Khomani, B. 1991 Stability of multilayer power law and second-order fluids in plane poiseuille flow. Chem. Engng Commun. 109 (1), 209–223.CrossRefGoogle Scholar
Su, Y.Y. & Khomami, B. 1992 Purely elastic interfacial instabilities in superposed flow of polymeric fluids. Rheol. Acta 31 (5), 413–420.CrossRefGoogle Scholar
Tsai, S.S.H., Wexler, J.S., Wan, J. & Stone, H.A. 2011 Conformal coating of particles in microchannels by magnetic forcing. Appl. Phys. Lett. 99 (15), 153509.CrossRefGoogle Scholar
Utada, A.S., Fernandez-Nieves, A., Gordillo, J.M. & Weitz, D.A. 2008 Absolute instability of a liquid jet in a coflowing stream. Phys. Rev. Lett. 100 (1), 014502.CrossRefGoogle Scholar
Wilson, G.M. & Khomami, B. 1992 An experimental investigation of interfacial instabilities in multilayer flow of viscoelastic fluids. J. Non-Newtonian Fluid Mech. 45 (3), 355–384.CrossRefGoogle Scholar
Yiantsios, S.G. & Higgins, B.G. 1988 Linear stability of plane poiseuille flow of two superposed fluids. Phys. Fluids 31 (11), 3225–3238.CrossRefGoogle Scholar
Yih, C.-S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27 (2), 337–352.CrossRefGoogle Scholar
Supplementary material: File

Hazra et al. supplementary movie

Observations of the unstable flow regimes: waviness along the interface and droplet formation from the low viscous fluid
Download Hazra et al. supplementary movie(File)
File 1.4 MB