Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-02T21:38:40.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Interactions of large-scale free-stream turbulence with turbulent boundary layers

Published online by Cambridge University Press:  01 August 2016

Eda Dogan ,
Ronald E. Hanson  and
Bharathram Ganapathisubramani
Eda Dogan*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
Ronald E. Hanson
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
Bharathram Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The scale interactions occurring within a turbulent boundary layer are investigated in the presence of free-stream turbulence. The free-stream turbulence is generated by an active grid. The free stream is monitored by a single-component hot-wire probe, while a second probe is roved across the height of the boundary layer at the same streamwise location. Large-scale structures occurring in the free stream are shown to penetrate the boundary layer and increase the streamwise velocity fluctuations throughout. It is speculated that, depending on the extent of the penetration, i.e. 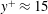based on the level of free-stream turbulence, the near-wall turbulence production peaks at different wall-normal locations than the expected location of $y^{+}\approx 15$ for a canonical turbulent boundary layer. It is shown that the large scales dominating the log region have a modulating effect on the small scales in the near-wall region; this effect becomes more significant with increasing turbulence in the free stream, i.e. similarly increasing 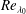$Re_{\unicode[STIX]{x1D706}_{0}}$. This modulating interaction and its Reynolds-number trend have similarities with canonical turbulent boundary layers at high Reynolds numbers where the interaction between the large scales and the envelope of the small scales exhibits a pure amplitude modulation (Hutchins & Marusic, Phil. Trans. R. Soc. Lond. A, vol. 365 (1852), 2007, pp. 647–664; Mathis et al., J. Fluid Mech., vol. 628, 2009, pp. 311–337). This similarity has encouraging implications towards generalising scale interactions in turbulent boundary layers.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 79 - 107
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Blair, M. F. 1983 Influence of free-stream turbulence on turbulent boundary layer heat transfer and mean profile development: part I. Experimental data. Trans. ASME: J. Heat Transfer 105, 33–40.CrossRefGoogle Scholar
Bruun, H. H. 1995 Hot-wire Anemometry: Principles and Signal Analysis. Oxford University Press.Google Scholar
Brzek, B., Torres-Nieves, S., Lebrón, J., Cal, R., Meneveau, C. & Castillo, L. 2009 Effects of free-stream turbulence on rough surface turbulent boundary layers. J. Fluid Mech. 635, 207–243.Google Scholar
Castro, I. P. 1984 Effects of free stream turbulence on low Reynolds number boundary layers. J. Fluids Engng 106, 298–306.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Coles, D. 1956 The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1, 191–226.Google Scholar
Duvvuri, S. & McKeon, B. J. 2015 Triadic scale interactions in a turbulent boundary layer. J. Fluid Mech. 767, R4.Google Scholar
Fernholz, H. & Finley, P. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.CrossRefGoogle Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hancock, P. E. & Bradshaw, P. 1983 The effect of free-stream turbulence on turbulent boundary layers. J. Fluids Engng 105 (3), 284–289.Google Scholar
Hancock, P. E. & Bradshaw, P. 1989 Turbulence structure of a boundary layer beneath a turbulent free stream. J. Fluid Mech. 205, 45–76.Google Scholar
Hearst, R. J., Buxton, O. R. H., Ganapathisubramani, B. & Lavoie, P. 2012 Experimental estimation of fluctuating velocity and scalar gradients in turbulence. Exp. Fluids 53 (4), 925–942.Google Scholar
Hearst, R. & Lavoie, P. 2015 The effect of active grid initial conditions on high Reynolds number turbulence. Exp. Fluids 56 (10), 1–20.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hutchins, N. & Marusic, I. 2007a Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hutchins, N. & Marusic, I. 2007b Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103.Google Scholar
Jacobi, I. & McKeon, B. J. 2011a Dynamic roughness perturbation of a turbulent boundary layer. J. Fluid Mech. 688, 258–296.Google Scholar
Jacobi, I. & McKeon, B. J. 2011b New perspectives on the impulsive roughness-perturbation of a turbulent boundary layer. J. Fluid Mech. 677, 179–203.Google Scholar
Jacobi, I. & McKeon, B. J. 2013 Phase relationships between large and small scales in the turbulent boundary layer. Exp. Fluids 54 (3), 1–13.Google Scholar
Jones, M. B., Marusic, I. & Perry, A. E. 2001 Evolution and structure of sink-flow turbulent boundary layers. J. Fluid Mech. 428, 1–27.CrossRefGoogle Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. J. Fluids Engng 132 (9), 094001.Google Scholar
Klewicki, J., Fife, P., Wei, T. & McMurtry, P. 2007 A physical model of the turbulent boundary layer consonant with mean momentum balance structure. Phil. Trans. R. Soc. Lond. A 365 (1852), 823–840.Google ScholarPubMed
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8(2) (1–4), 53.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011a A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011b The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23 (12), 121702.Google Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692–701.Google Scholar
Monkewitz, P. A., Chauhan, K. A. & Nagib, H. M. 2008 Comparison of mean flow similarity laws in zero pressure gradient turbulent boundary layers. Phys. Fluids 20 (10), 105102.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.CrossRefGoogle Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Karman coefficient in canonical flows. Phys. Fluids 20 (10), 101518.Google Scholar
Patel, V. C. 1965 Calibration of the Preston tube and limitations on its use in pressure gradients. J. Fluid Mech. 23, 185–208.Google Scholar
Perry, A. E. & Li, J. D. 1990 Experimental support for the attached-eddy hypothesis in zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 218, 405–438.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22 (5), 051704.Google Scholar
Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2009 Effects of large-scale free stream turbulence on a turbulent boundary layer. Phys. Fluids 21 (9), 095105.CrossRefGoogle Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Stefes, B. & Fernholz, H.-H. 2004 Skin friction and turbulence measurements in a boundary layer with zero-pressure-gradient under the influence of high intensity free-stream turbulence. Eur. J. Mech. (B/Fluids) 23 (2), 303–318.Google Scholar
Thole, K. A. & Bogard, D. G. 1996 High freestream turbulence effects on turbulent boundary layers. J. Fluids Engng 118, 276–284.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.CrossRefGoogle Scholar