Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T23:30:10.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Interactions between a shock and turbulent features in a Mach 2 compressible boundary layer

Published online by Cambridge University Press:  22 April 2020

R. Baidya Open the ORCID record for R. Baidya [Opens in a new window] ,
S. Scharnowski ,
M. Bross Open the ORCID record for M. Bross [Opens in a new window]  and
C. J. Kähler
R. Baidya*
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Bundeswehr University Munich, Werner-Heisenberg-Weg 39, 85577Neubiberg, Germany
S. Scharnowski
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Bundeswehr University Munich, Werner-Heisenberg-Weg 39, 85577Neubiberg, Germany
M. Bross
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Bundeswehr University Munich, Werner-Heisenberg-Weg 39, 85577Neubiberg, Germany
C. J. Kähler
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Bundeswehr University Munich, Werner-Heisenberg-Weg 39, 85577Neubiberg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

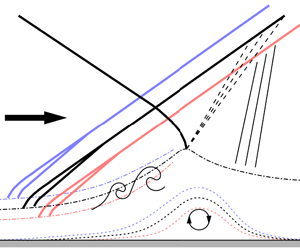
Large field-of-view (FOV) particle image velocimetry experiments are conducted in the vicinity of a shock wave boundary layer interaction (SWBLI) at Mach 2. The current FOV covers up to 30 boundary layer thicknesses ($\widehat{\unicode[STIX]{x1D6FF}}_{I}$), comprising of upstream and downstream regions relative to the SWBLI, thereby allowing the turbulent boundary layer and shock to be simultaneously captured. The relationship between the boundary layer features and the instantaneous shock location is directly quantified, with the aim of better understanding the mechanisms responsible for oscillation of the reflected shock. The results show that the reflected shock location is clearly influenced by the instantaneous state of the incoming boundary layer. It is found that passage of low-/high-momentum very-large-scale turbulent features through the SWBLI region causes the reflected shock to move upstream/downstream of the mean location. Moreover, interaction with the shock is found to introduce additional velocity fluctuations across a range of spanwise length scales within the boundary layer. The spanwise scales smaller than one $\widehat{\unicode[STIX]{x1D6FF}}_{I}$ recover within one $\widehat{\unicode[STIX]{x1D6FF}}_{I}$ downstream of the SWBLI region. However, at larger spanwise wavelengths, two persistent modes at approximately one and six $\widehat{\unicode[STIX]{x1D6FF}}_{I}$ are observed, where they remain correlated for a longer streamwise extent ($\gg \widehat{\unicode[STIX]{x1D6FF}}_{I}$) than the other spanwise modes. The wall pressure measurements indicate that the low-frequency fluctuations arising from the oscillating shock foot are due to dampening of high-frequency contents beyond the critical frequency associated with the unstable global mode. Thus, the results suggest that low-frequency pressure oscillations are not necessarily an independent phenomenon from the turbulent features entering the SWBLI region and interacting with the shock. Instead, a large scale separation between their dominant time scales is due to the critical frequency of the unstable global mode occurring at frequencies that are orders of magnitudes slower than the dominant frequency of the very-large-scale features.

JFM classification

Compressible Flows: Compressible boundary layers Compressible Flows: Shock waves Turbulent Flows: Compressible turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A15
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baars, W. J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Baidya, R., Scharnowski, S., Bross, M. & Kähler, C. J. 2019 Relationship between boundary layer features and shock reflection. In Proceedings of the 13th International Symposium on Particle Image Velocimetry. Bundeswehr University Munich.Google Scholar
Bendat, J. S. & Piersol, A. G. 2010 Random Data: Analysis and Measurement Procedures, 4th edn. John Wiley & Sons.CrossRefGoogle Scholar
Beresh, S. J., Clemens, N. T. & Dolling, D. S. 2002 Relationship between upstream turbulent boundary-layer velocity fluctuations and separation shock unsteadiness. AIAA J. 40 (12), 2412–2422.CrossRefGoogle Scholar
Bross, M., Fuchs, T. & Kähler, C. J. 2019a Interaction of coherent flow structures in adverse pressure gradient turbulent boundary layers. J. Fluid Mech. 873, 287–321.CrossRefGoogle Scholar
Bross, M., Scharnowski, S. & Kähler, C. J. 2019b Large scale coherent structures in a ZPG turbulent boundary layer for the Mach number range 0.3–3.0. In Proceedings of the 11th International Symposium on Turbulence and Shear Flow Phenomena.Google Scholar
Chauhan, K. A., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.CrossRefGoogle Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.CrossRefGoogle Scholar
Dolling, D. S. & Erengil, M. E. 1991 Unsteady wave structure near separation in a Mach 5 compression ramp interaction. AIAA J. 29 (5), 728–735.Google Scholar
van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Spacecr. Rockets 18 (3), 145–160.Google Scholar
Dupont, P., Haddad, C. & Debieve, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.CrossRefGoogle Scholar
Fernholz, H. H. & Finley, P. J.1980 A critical commentary on mean flow data for two-dimensional compressible turbulent boundary layers. Tech. Rep. AGARD-AG-253. AGARD.Google Scholar
Fernholz, H. H. & Finleyt, P. J. 1996 The incompressible zero-pressure-gradient turbulent boundary layer: an assessment of the data. Prog. Aerosp. Sci. 32 (4), 245–311.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.CrossRefGoogle Scholar
Grayson, K., de Silva, C. M., Hutchins, N. & Marusic, I. 2018 Impact of mismatched and misaligned laser light sheet profiles on PIV performance. Exp. Fluids 59 (1), 2.CrossRefGoogle Scholar
Grilli, M., Schmid, P. J., Hickel, S. & Adams, N. A. 2012 Analysis of unsteady behaviour in shockwave turbulent boundary layer interaction. J. Fluid Mech. 700, 16–28.CrossRefGoogle Scholar
Hampel, A.1984 Auslegung, Optimierung und Erprobung eines vollautomatisch arbeitenden Transsonik-Windkanals. PhD thesis, Hochschule der Bundeswehr.Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & Van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.CrossRefGoogle Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.CrossRefGoogle Scholar
Kähler, C. J., Sammler, B. & Kompenhans, J. 2002 Generation and control of particle size distributions for optical velocity measurement techniques in fluid mechanics. Exp. Fluids 33, 736–742.CrossRefGoogle Scholar
Kähler, C. J., Scharnowski, S. & Cierpka, C. 2012 On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52 (6), 1641–1656.CrossRefGoogle Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Krogstad, P. Å., Antonia, R. A. & Browne, L. W. B. 1992 Comparison between rough-and smooth-wall turbulent boundary layers. J. Fluid Mech. 245, 599–617.CrossRefGoogle Scholar
Lee, J. H., Kevin, Monty, J. P. & Hutchins, N. 2016 Validating under-resolved turbulence intensities for PIV experiments in canonical wall-bounded turbulence. Exp. Fluids 57 (8), 129.CrossRefGoogle Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurments of turbulence in the viscous sublayer using subminature hot-wire probes. Exp. Fluids 5, 407–417.CrossRefGoogle Scholar
Marusic, I., Chauhan, K. A., Kulandaivelu, V. & Hutchins, N. 2015 Evolution of zero-pressure-gradient boundary layers from different tripping conditions. J. Fluid Mech. 783, 379–411.CrossRefGoogle Scholar
Morkovin, M. V. 1962 Effects of compressibility on turbulent flows. In Mécanique de la Turbulence (ed. Favre, A. J.), pp. 367–380. CNRS.Google Scholar
Muck, K., Bogdonoff, S. & Dussauge, J. P. 1985 Structure of the wall pressure fluctuations in a shock-induced separated turbulent flow. In 23rd Aerospace Sciences Meeting, 179. AIAA.Google Scholar
Pasquariello, V., Hickel, S. & Adams, N. A. 2017 Unsteady effects of strong shock-wave/boundary-layer interaction at high Reynolds number. J. Fluid Mech. 823, 617–657.CrossRefGoogle Scholar
Piponniau, S., Dussauge, J. P., Debieve, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
Pirozzoli, S. & Bernardini, M. 2011 Turbulence in supersonic boundary layers at moderate Reynolds number. J. Fluid Mech. 688, 120–168.CrossRefGoogle Scholar
Pirozzoli, S. & Grasso, F. 2006 Direct numerical simulation of impinging shock wave/turbulent boundary layer interaction at M = 2. 25. Phys. Fluids 18 (6), 065113.CrossRefGoogle Scholar
Pirozzoli, S., Larsson, J., Nichols, J. W., Bernardini, M., Morgan, B. E. & Lele, S. K. 2010 Analysis of unsteady effects in shock/boundary layer interactions. In Center for Turbulence Research Proceedings of the Summer Program, pp. 153–164. Center for Turbulence Research.Google Scholar
Priebe, S. & Martín, M. P. 2012 Low-frequency unsteadiness in shock wave–turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.CrossRefGoogle Scholar
Raffel, M., Willert, C. E., Scarano, F., Kähler, C. J., Wereley, S. T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Ren, J. & Fu, S. 2015 Secondary instabilities of Görtler vortices in high-speed boundary layer flows. J. Fluid Mech. 781, 388–421.CrossRefGoogle Scholar
Reuther, N. & Kähler, C. J. 2018 Evaluation of large-scale turbulent/non-turbulent interface detection methods for wall-bounded flows. Exp. Fluids 59 (7), 121.CrossRefGoogle Scholar
Scharnowski, S., Bross, M. & Kähler, C. J. 2019 Accurate turbulence level estimations using PIV/PTV. Exp. Fluids 60 (1), 1.CrossRefGoogle Scholar
Settles, G. S. & Dodson, L. J.1994a Hypersonic shock/boundary-layer interaction database: new and corrected data. NASA Tech. Rep. CR-177638.CrossRefGoogle Scholar
Settles, G. S. & Dodson, L. J. 1994b Supersonic and hypersonic shock/boundary-layer interaction database. AIAA J. 32 (7), 1377–1383.CrossRefGoogle Scholar
Smits, A. J & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer Science and Business Media.Google Scholar
Spall, R. E. & Malik, M. R. 1989 Goertler vortices in supersonic and hypersonic boundary layers. Phys. Fluids 1 (11), 1822–1835.CrossRefGoogle Scholar
Theunissen, R., Scarano, F. & Riethmuller, M. L. 2008 On improvement of PIV image interrogation near stationary interfaces. Exp. Fluids 45 (4), 557–572.CrossRefGoogle Scholar
Thomas, F. O., Putnam, C. M. & Chu, H. C. 1994 On the mechanism of unsteady shock oscillation in shock wave/turbulent boundary layer interactions. Exp. Fluids 18 (1–2), 69–81.CrossRefGoogle Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow, 2nd edn. Cambridge University Press.Google Scholar
Ünalmis, O. H. & Dolling, D. S. 1998 Experimental study of causes of unsteadiness of shock-induced turbulent separation. AIAA J. 36 (3), 371–378.CrossRefGoogle Scholar
Vanstone, L. & Clemens, N. T. 2019 Proper orthogonal decomposition analysis of swept-ramp shock-wave/boundary-layer unsteadiness at Mach 2. AIAA J. 57 (8), 3395–3409.CrossRefGoogle Scholar
Walz, A. 1959 Compressible turbulent boundary layers with heat transfer and pressure gradient in flow direction. J. Res. Natl Bur. Stand. 63B, 53–70.Google Scholar