Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-01T03:45:53.090Z Has data issue: false hasContentIssue false
  • English
  • Français

Interaction of instability waves and a three-dimensional roughness element in a boundary layer

Published online by Cambridge University Press:  06 July 2017

I. B. de Paula Open the ORCID record for I. B. de Paula [Opens in a new window] ,
W. Würz ,
M. T. Mendonça  and
M. A. F. Medeiros
I. B. de Paula*
Affiliation:
Departamento de Engenharia Mecânica, Pontifícia Universidade Católica do Rio de Janeiro, PUC-Rio, Rua Marquês de São Vicente 225, 22451-041, Brazil
W. Würz
Affiliation:
Institut für Aerodynamik und Gasdynamik, Universität Stuttgart, Pfaffenwaldring 21, 70550 Stuttgart, Germany
M. T. Mendonça
Affiliation:
Instituto de Aeronáutica e Espaço, CTA/IAE/APA, 12228904 São José dos Campos, Brasil
M. A. F. Medeiros
Affiliation:
Departamento de Engenharia Aeronáutica, Escola de Engenharia de São Carlos, Universidade de São Paulo, 13566-590, Brazil
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of a single roughness element on the evolution of two-dimensional (2-D) Tollmien–Schlichting (TS) waves is investigated experimentally. Experiments are carried out in a region of zero pressure gradient of an airfoil section. Downstream from the disturbance source, TS waves interact with a cylindrical roughness element with a slowly oscillating height. The oscillation frequency of the roughness was approximately 1500 times lower than the wave frequency and approximately 250 times slower than the characteristic time of flow passing the region of transition development. Therefore, the roughness behaved as a quasi-steady disturbance. The set-up enabled us to perform hot-wire measurements phase locked to the waves and to the roughness movement. Experimental results show a scattering of the 2-D waves into oblique ones and a relatively weak distortion of the mean flow for roughness heights as large as 0.2 times the boundary layer displacement thickness (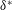$\unicode[STIX]{x1D6FF}^{\ast }$). Transfer functions for TS wave scattering at the roughness are obtained. Results show an unexpected coincidence in shape with acoustic receptivity functions found in Würz et al. (J. Fluid Mech., vol. 478, 2003, pp. 135–163) for the problem of excitation of TS waves by scattering of acoustic waves at surface roughness. In the present work, the ratio between the incoming 2-D wave amplitude to the amplitude of the scattered oblique waves scaled linearly with the roughness height only for very shallow roughness. For roughness elements higher than 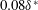$0.08\unicode[STIX]{x1D6FF}^{\ast }$ and below 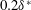$0.2\unicode[STIX]{x1D6FF}^{\ast }$, the wave scattering exhibited a quadratic variation with respect to the roughness height. In addition, this feature did not vary significantly with respect to TS wave frequency. An analysis of the weakly nonlinear interactions triggered by the roughness element is also carried out, assisted by numerical solution of nonlinear parabolized stability equations, performed for a two-dimensional Blasius boundary layer. A comparison between experiments and simulations reveals that the weakly nonlinear interactions observed are not substantially affected by mean flow distortions that could be produced in the wake of the small and medium sized roughness elements (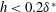$h<0.2\unicode[STIX]{x1D6FF}^{\ast }$). From a practical perspective, results suggest that scattering coefficients might be employed to include the effect of isolated and medium sized roughness elements in transition prediction tools developed for smooth surfaces.

JFM classification

Boundary Layers: Boundary Layers Boundary Layers: Boundary layer receptivity Boundary Layers: Boundary layer stability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , pp. 624 - 660
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acarlar, M. & Smith, C. 1992 A study of hairpin vortices in a laminary boudary layer. Part 1. Hairpin vortices generated by a hemisphere protuberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Andersson, P., Brand, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Bernardini, M., Pirozzoli, S., Orlandi, P. & Lele, S. 2014 Parametrization of boundary-layer transition induced by isolated roughness elements. AIAA J. 52 (10), 2261–2269.Google Scholar
Bertolotti, F. P., Herbert, T. & Sparlat, P. R. 1992 Linear and nonlinear stability of the Blasius boundary layer. J. Fluid Mech. 242, 441–474.Google Scholar
Cebeci, T. & Smith, A. M. O. 1974 Analysis of Turbulent Boundary Layers. Academic Press.Google Scholar
Choudhari, M. & Streett, C. 1992 A finite Reynolds number approach for the prediction of boundary-layer receptivity in localized regions. Phys. Fluids A 4, 2495–2514.Google Scholar
Cossu, C. & Brandt, L. 2004 On Tollmien-Schlichting-like waves in streaky boundary layers. Eur. J. Mech. (B/Fluids) 23, 815–833.Google Scholar
Crouch, J. D.1994 Theoretical studies on the receptivity of boundary layers. AIAA Paper 94-2224.CrossRefGoogle Scholar
Crouch, J. D. 1997 Excitation of secondary instabilities in boundary layers. J. Fluid Mech. 336, 245–266.CrossRefGoogle Scholar
Crouch, J. D. & Ng, L. L. 2000 Variable n-factor method for transition prediction in three-dimensional boundary layers. AIAA J. 38 (2), 211–216.Google Scholar
Denissen, N. & White, E. B. 2013 Secondary instability of roughness-induced transient growth. Phys. Fluids 25, 114108.Google Scholar
Dovgal, A. V. & Kozlov, V. V. 1990 Hydrodynamic instability and receptivity of small scale separtion regions. In IUTAM Symposium on Laminar–Turbulent Transition (ed. Arnal, D. & Michel, R.). Springer.Google Scholar
Drela, M. & Giles, M. B.1986 Viscous-inviscid analysis of transonic and low Reynolds number airfoils. AIAA 86-1786-CP.CrossRefGoogle Scholar
Dryden, H. L. 1953 Review of published data on the effect of roughness on transition from laminar to turbulent flow. J. Aero. Sci. 20 (7), 477–482.Google Scholar
Ergin, F. G. & White, E. B. 2006 Unsteady and transitional flows behind roughness elements. AIAA J. 44 (11), 2504–2514.CrossRefGoogle Scholar
Fage, A. 1943 The smallest size of a spanwise surface corrugation which affects boundary layer transition on an airfoil. Aero. Res. Counc. R&M 2120.Google Scholar
Fransson, J. H. M., Brandt, L., Talamelli, A. & Cossu, C. 2005 Experimental study of the stabilization of Tollmien-Schlichting waves by finite amplitude streaks. Phys. Fluids 17, 054110.CrossRefGoogle Scholar
Gaster, M., Grosch, C. E. & Jackson, T. L. 1994 Velocity field created by a shallow bump in a boundary layer. Phys. Fluids 6 (9), 3079–3085.CrossRefGoogle Scholar
Gregory, N. & Walker, W. 1956 The effect on transition of isolated suface excrescences in the boundary layer. Aero. Res. Counc. R&M 2779.Google Scholar
Herbert, T. 1988 Secondary instability of boundary-layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Jacobs, E. N.1939 Preliminary report on laminar-flow airfoils and new methods adopted for airfoil and boundary-layer investigations. Tech. Rep. 345. NACA WR L.Google Scholar
Kachanov, Y. S. 2000 Three-dimensional receptivity of boundary layers. Eur. J. Mech. (B/Fluids) 19, 723–744.Google Scholar
Kegerise, M. A., King, R. A., Choudhari, M., Li, F. & Norris, A.2014 An experimental study of roughness-induced instabilities in a supersonic boundary layer. AIAA Paper 2014-2501.CrossRefGoogle Scholar
Kendall, J. M.1981 Laminar boundary layer velocity distortion by surface roughness: effect upon stability. AIAA Paper 1981-0195.Google Scholar
Klebanoff, P. S., Cleveland, W. G. & Tidstrom, K. D. 1992 On the evolution of a turbulent boundary layer induced by a three-dimensional roughness element. J. Fluid Mech. 237, 101–187.CrossRefGoogle Scholar
Klebanoff, P. S., Schubauer, G. B. & Tidstrom, K. D. 1954 Measurements of the effect of two-dimensional and three-dimensional roughness elements on boundary-layer transition. J. Aero. Sci. 21 (1), 62–65.Google Scholar
Klebanoff, P. S. & Tidstrom, K. D. 1972 Mechanism by wich a two-dimensional roughness element induces boundary-layer transition. Phys. Fluids 15 (17), 1173–1188.CrossRefGoogle Scholar
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary-layer instability. J. Fluid Mech. 12, 1–34.CrossRefGoogle Scholar
Legendre, R. & Werlé, H. 2001 Toward elucidation of three-dimensional separation. Annu. Rev. Fluid Mech. 33, 129–154.Google Scholar
Loiseau, J. C., Robinet, J. C., Cherubini, S. & Leriche, E. 2014 Investigation of the roughness-induced transition: global stability analyses and direct numerical simulations. J. Fluid Mech. 760, 175–211.CrossRefGoogle Scholar
Mendonca, M. T.1997 Numerical analisys of Görtler vortices Tollmien–Schlichting waves interaction with a spatial nonparalel model. PhD thesis, The PennState University, US.Google Scholar
Mochizuki, M. 1961 Smoke observation on bounary layer transition caused by a spherical roughness element. J. Phys. Soc. Japan 16, 995–1008.Google Scholar
Morkovin, M. V. 1990 On the roughness-induced transition: facts, view and speculations. In Stability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), vol. 1. Springer.Google Scholar
de Paula, I. B., Medeiros, M. A. F. & Würz, W. 2008 Experimental study of a Tollmien–Schlichting wave interacting with a shallow 3-d roughness element. J. Turbul. 9 (7), 1–23.Google Scholar
de Paula, I. B., Würz, W., Kämer, E., Borodulin, V. I. & Kachanov, Y. S. 2013 Weakly nonlinear stages of boundary-layer transition initiated by modulated Tollmien–Schlichting waves. J. Fluid Mech. 732, 571–615.Google Scholar
Plogmann, B., Würz, W. & Krämer, E. 2014 On the disturbance evolution downstream of a cylindrical roughness element. J. Fluid Mech. 758, 238–286.Google Scholar
Reshotko, E. & Tumin, A. 2004 Role of transient growth in roughness-induced transition. AIAA J. 8, 311–349.Google Scholar
Rist, U. & Jäger, A. 2004 Unsteady disturbance generation and amplification in the boundary-layer flow behind a medium sized roughness element. In IUTAM Symposium on Laminar-Turbulent Transition.Google Scholar
Saric, W. S., Hoos, J. A. & Radeztsky, R. H. 1991 Boundary layer receptivity to sound with roughness. In Boundary Layer Stability and Transition to Turbulence (ed. Reda, D. C., Reed, H. L. & Kobayashi, R.). ASME-FED.Google Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.Google Scholar
Tani, I. 1961 Effect of two-dimensional and isolated roughness on laminar flow. Boundary Layer and Flow Control. vol. 2, pp. 637–656. Pergamon.Google Scholar
Tani, I. 1969 Boundary layer transition. Annu. Rev. Fluid Mech. 1, 169–196.CrossRefGoogle Scholar
Tani, I. & Hama, R. 1940 On the permissible roughness in the laminar boundary layer. Rep. Aeronautical Research Inst. of Tokyo Imperial University 199, 419–429.Google Scholar
Tobak, M. & Peake, D. J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14, 61–85.Google Scholar
Tulio, N. D. & Sandham, N. D. 2015 Roughness-induced instability in high speed boundary layer. J. Fluid Mech. 763, 136–165.Google Scholar
Ustinov, M. V. 1995 Secondary instability modes generated by Tollmien–Schlichting wave scattering from a bump. Theor. Comput. Fluid Dyn. 7, 341–354.CrossRefGoogle Scholar
Wang, Y. X.2004 Instability and transition of boundary layer flows disturbed by steps and bumps. PhD thesis, Queen Mary College, University of London, UK.Google Scholar
Wortmann, F. X. & Althaus, D. 1964 Der laminarwindkanal des instituts fur aerodynamik und gasdynamik der technischen hochschule stuttgart. Z. Flugwiss. 12 (4), 129–134.Google Scholar
Wu, X. & Hogg, L. W. 2006 Acoustic radiation of Tollmien–Schlichting waves as they undergo rapid distortion. J. Fluid Mech. 550, 307–347.CrossRefGoogle Scholar
Würz, W., Herr, S., Wörner, A., Rist, U., Wagner, S. & Kachanov, Y. S. 2003 Three-dimensional acoustic-receptivity of a boundary layer on an airfoil: experiments and direct numerical simulations. J. Fluid Mech. 478, 135–163.Google Scholar
Würz, W., Sartorius, D., Wagner, S., Borodulin, V. I. & Kachanov, Y. S. 2004 Experimental study of weakly nonlinear interactions of instability waves in a non self-similar boundary layer on an airfoil – Part I: base flow and initially tuned resonances. In 12th International Conference on Methods of Aerophysical Research – ICMAR2004, Novosibirsk.Google Scholar
Zelman, M. B. & Maslennikova, I. I. 1993 Tollmien–Schlichting-wave resonant mechanism for subharmonic-type transition. J. Fluid Mech. 252, 449–478.Google Scholar