Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T03:20:38.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Instantaneous pressure measurements on a spherical grain under threshold flow conditions

Published online by Cambridge University Press:  07 February 2014

Ahmet O. Celik ,
P. Diplas  and
C. L. Dancey
Ahmet O. Celik*
Affiliation:
Department of Civil Engineering, Anadolu University, Eskisehir, 26555, Turkey
P. Diplas
Affiliation:
Imbt Environmental Hydraulics Laboratory, Department of Civil and Environmental Engineering, Lehigh University, Bethlehem, PA 18015-3176, USA
C. L. Dancey
Affiliation:
Baker Environmental Hydraulics Laboratory, Department of Mechanical Engineering, Virginia Tech, Blacksburg, VA 24061, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this investigation was to experimentally examine the surface pressures and resulting forces on an individual sediment grain whose size is comparable to the scales of the turbulent channel flow in an effort to discern details of the flow/grain interaction. This was accomplished by measuring the pressure fluctuations on the surface of a coarse, fully exposed, spherical grain resting upon a bed of identical grains in open channel turbulent flow. This spherical particle was instrumented with low-range, high-frequency-response pressure transducers to measure the individual surface pressures simultaneously on its front, back, top and bottom. The local flow velocity was measured synchronously with a laser Doppler velocimeter. The flow and sediment are near threshold conditions for entrainment with the channel and particle Reynolds numbers varying between 31 000–39 000 and 330–440 respectively. The emphasis was on determining the characteristics of the flow field with the potential to dislodge a spherical grain under uniform flow conditions as well as in the wake of a circular cylinder placed spanwise across the flow in otherwise fully developed open channel flow. It is concluded that the streamwise velocity near the bed is most directly related to those force events (and associated individual surface pressure distributions) crucial for particle entrainment. The lift force was observed to momentarily reach values which can be consequential for particle stability, although it is poorly correlated with the fluctuating normal velocity component. Turbulence intensity near the bed, rather than being the causative factor for increased force fluctuations, was shown to be an indicator of changes in the average lift force experienced by the grain during the application of extreme drag forces, at least for this particular flow condition (the upstream, spanwise-mounted circular cylinder). This effect is known to alter the sediment transport rates significantly. The characteristics of the temporal durations of flow events about the local maxima in the stagnation pressure, drag and lift forces, using a conditional sampling method, revealed the prevalence of sweep-type near-bed flow events in generating favourable conditions for particle dislodgement, although the dominant feature is the positive streamwise velocity fluctuation, not the normal velocity component. The duration of such events was the highest in the fourth and first quadrants in the 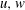$u,w$ plane, inducing high impulses on the grain.

JFM classification

Geophysical and Geological Flows: River dynamics Geophysical and Geological Flows: Sediment transport Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 60 - 97
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancey, C., Bohm, T., Jodeau, M. & Frey, P. 2006 Statistical description of sediment transport experiments. Phys. Rev. E 74 (1), 1–14.Google Scholar
Balakrishnan, M.1997 The role of turbulence on the entrainment of a single sphere and the effects of roughness on fluid-solid interaction. PhD thesis, Virginia Polytechnic Institute and State University.Google Scholar
Brayshaw, A. C., Frostick, L. E. & Reid, I. 1983 The hydrodynamics of particle clusters and sediment entrapment in coarse alluvial channels. Sedimentology 30 (1), 137–143.CrossRefGoogle Scholar
Bushnell, D. M. & McGinley, C. B. 1989 Turbulence control in wall flows. Annu. Rev. Fluid Mech. 21, 1–20.Google Scholar
Cameron, S. M.2006 Near-boundary flow structure and particle entrainment. PhD thesis, University of Auckland.Google Scholar
Celik, A. O.2011 Experimental investigation of the role of turbulence fluctuations on incipient motion of sediment. PhD thesis, Virginia Polytechnic Institute and State University.Google Scholar
Celik, A. O., Diplas, P., Dancey, C. L. & Valyrakis, M. 2010 Impulse and particle dislodgement under turbulent flow conditions. Phys. Fluids 22, 046601.CrossRefGoogle Scholar
Cheng, N. S., Law, A. W. K. & Lim, S. Y. 2003 Probability distribution of bed particle instability. Adv. Water Resour. 26 (4), 427–433.Google Scholar
Derksen, J. J. & Larsen, R. A. 2011 Drag and lift forces on random assemblies of wall-attached spheres in low-Reynolds number shear flow. J. Fluid Mech. 673, 548–573.Google Scholar
Detert, M., Nikora, V. & Jirka, G. H. 2010a Synoptic velocity and pressure fields at the water-sediment interface of streambeds. J. Fluid Mech. 660, 55–86.CrossRefGoogle Scholar
Detert, M., Weitbrecht, V. & Jirka, G. H. 2010b Laboratory measurements on turbulent pressure fluctuations in and above gravel beds. J. Hydraul. Engng 136, 779–789.CrossRefGoogle Scholar
Diplas, P., Dancey, C. L., Celik, A. O., Valyrakis, M., Greer, K. & Akar, T. 2008 The role of impulse on the initiation of particle movement under turbulent flow conditions. Science 322, 717–720.Google Scholar
Dwivedi, A., Melville, B. & Shamseldin, A. Y. 2010a Hydrodynamic forces generated on a spherical sediment particle during entrainment. J. Hydraul. Engng 136 (10), 756–769.CrossRefGoogle Scholar
Dwivedi, A., Melville, B., Shamseldin, A. Y. & Guha, T. K. 2010b Drag force on a sediment particle from point velocity measurements: a spectral approach. Water Resour. Res. 46, W10529.CrossRefGoogle Scholar
Dwivedi, A., Melville, B., Shamseldin, A. Y. & Guha, T. K. 2011 Flow structures and hydrodynamic force during sediment entrainment. Water Resour. Res. 47, W01509.Google Scholar
Einstein, H. A. & El-Samni, E. A. 1949 Hydrodynamic forces on a rough wall. Rev. Mod. Phys. 21 (3), 520–524.Google Scholar
Heathershaw, A. D. & Thorne, P. D. 1985 Sea-bed noises reveal role of turbulent bursting phenomenon in sediment transport by tidal currents. Nature 316, 339–342.Google Scholar
Hofland, B.2005 Rock and roll turbulence-induced damage to granular bed protections. PhD thesis, TU Delft, www.library.tudelft.nl.Google Scholar
Hofland, B. & Battjes, J. 2006 Probability density function of instantaneous drag forces and shear stresses on a bed. J. Hydraul. Engng 132, 1169–1175.Google Scholar
Hofland, B., Booij, R. & Battjes, J. 2005 Measurement of fluctuating pressures on coarse bed material. J. Hydraul. Engng 131 (9), 770–781.Google Scholar
Jackson, R. G. 1976 Sedimentological and fluid-dynamic implications of the turbulent bursting phenomenon in geophysical flows. J. Fluid Mech. 77, 531–560.CrossRefGoogle Scholar
Johansson, A. V., Her, J. Y. & Haritonidis, J. H. 1987 On the generation of high-amplitude wall-pressure peaks in turbulent boundary layers and spots. J. Fluid Mech. 175, 119–142.Google Scholar
Kalinske, A. A. 1947 Movement of sediment as bed load in rivers. Trans. AGU 28 (4), 615–620.Google Scholar
Keshavarzi, A. R. & Gheisi, A. R. 2006 Stochastic nature of three-dimensional bursting events and sediment entrainment in vortex chamber. Stoch. Env. Res. Risk A. 21 (1), 75–87.Google Scholar
Kirchner, J. W., Dietrich, W. E., Iseya, F. & Ikeda, H. 1990 The variability of critical shear stress, friction angle, and grain protrusion in water-worked sediments. Sedimentology 37, 647–672.Google Scholar
Laadhari, F., Morel, R. & Alcaraz, E. 1994 Combined visualisation and measurements in transitional boundary layers. Eur. J. Mech. (B-Fluids) 13 (4), 473–489.Google Scholar
Ling, C. H. 1995 Criteria for incipient motion of spherical sediment particles. J. Hydraul. Engng 121 (6), 472–478.CrossRefGoogle Scholar
Nelson, J. M., Shreve, R. L., MacLean, S. R. & Drake, T. G. 1995 Role of near-bed turbulence structure in bed load transport and bed form mechanics. Water Resour. Res. 31 (8), 2071–2086.Google Scholar
Nezu, I. & Nakagawa, H. 1993 In Turbulence in Open Channel Flows IAHR Monograph, Balkema.Google Scholar
Paiement-Paradis, G., Marquis, G. & Roy, A. 2010 Effects of turbulence on the transport of individual particles as bedload in a gravel-bed river. Earth Surf. Process. Landf. 36, 107–116.Google Scholar
Paintal, A. S. 1971 Concept of critical shear stress in loose boundary open channels. J. Hydraul. Engng Div. ASCE 9, 91–114.Google Scholar
Papanicolaou, A. N., Diplas, P., Evaggelopoulos, N. & Fotopoulos, S. 2002 Stochastic incipient motion criterion for spheres under various bed packing conditions. J. Hydraul. Engng 128 (4), 369–380.Google Scholar
van Radecke, H. & Schulz-DuBois, E. O. 1988 Linear response of fluctuating forces to turbulent velocity components. In Fourth International Symposium on Applications of Laser-Doppler Anemometry to Fluid Mechanics (ed. Adrian, R. J.), pp. 23–44. Springer.Google Scholar
Radspinner, R., Diplas, P., Lightbody, A. & Sotiropoulos, F. 2010 River training and ecological enhancement using in-stream structures. J. Hydraul. Engng 136 (12), 967–980.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 22, 631–639.Google Scholar
Schmeeckle, M. W. & Nelson, J. M. 2003 Direct numerical simulation of bedload transport using a local dynamic boundary condition. Sedimentology 50, 279–301.Google Scholar
Schmeeckle, M. W., Nelson, J. M. & Shreve, R. L. 2007 Forces on stationary particles in near-bed turbulent flows. J. Geophys. Res. 112, 279–301.Google Scholar
Shvidchenko, A. B. & Pender, G. 2001 Macroturbulent structure of open-channel flow over gravel beds. Water Resour. Res. 37 (3), 709–719.Google Scholar
Smart, G. M. & Habersack, H. M. 2007 Pressure fluctuations and gravel entrainment in rivers. J. Hydraul. Res. 45 (5), 661–673.Google Scholar
Song, T., Graf, W. H. & Lemmin, U. 1994 Uniform flow in open channels with movable gravel bed. J. Hydraul. Res. 32 (2), 861–876.Google Scholar
Stoesser, T., Frohlich, J. & Rodi, W. 2007 Turbulent open-channel flow over a permeable bed. In Proceedings of 32nd IAHR Congress, Venice, Italy .Google Scholar
Sumer, B. M., Chua, L. H. C., Cheng, N. S. & Fredsoe, J. 2003 Uniform flow in open channels with movable gravel bed. J. Hydraul. Res. 32 (2), 861–876.Google Scholar
Sumer, B. M. & Fredsoe, E. J. 2006 Hydrodynamics Around Cylindrical Structures. World Scientific.Google Scholar
Sutherland, A. J. 1967 Proposed mechanism for sediment entrainment by turbulent flows. J. Geophys. Res. 72 (24), 6183–6194.Google Scholar
Valyrakis, M., Diplas, P., Dancey, C. L., Greer, K. & Celik, A. O. 2010 The role of instantaneous force magnitude and duration on particle entrainment. J. Geophys. Res. 115 (F02006).Google Scholar
Vollmer, S. & Kleinhans, M. G. 2007 Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resour. Res. 43 (W05410).Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Yoshida, A., Tamura, Y. & Kurita, T. 2001 Effects of bends in a tubing system for pressure measurement. J. Wind Engng Ind. Aerodyn. 89 (20), 1701–1716.Google Scholar
Zeng, L., Balachandar, S., Fischer, P. & Najjar, F. 2008 Interactions of a stationary finite-sized particle with wall turbulence. J. Fluid Mech. 594, 271–305.Google Scholar