Article contents
Instantaneous energy and enstrophy variations in Euler-alpha point vortices via triple collapse
Published online by Cambridge University Press: 21 May 2012
Abstract
It has been pointed out that the anomalous enstrophy dissipation in non-smooth weak solutions of the two-dimensional Euler equations has a clue to the emergence of the inertial range in the energy density spectrum of two-dimensional turbulence corresponding to the enstrophy cascade as the viscosity coefficient tends to zero. However, it is uncertain how non-smooth weak solutions can dissipate the enstrophy. In the present paper, we construct a weak solution of the two-dimensional Euler equations from that of the Euler- equations proposed by Holm, Marsden & Ratiu (Phys. Rev. Lett., vol. 80, 1998, pp. 4173–4176) by taking the limit of
equations proposed by Holm, Marsden & Ratiu (Phys. Rev. Lett., vol. 80, 1998, pp. 4173–4176) by taking the limit of 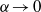 . To accomplish this task, we introduce the
. To accomplish this task, we introduce the  -point-vortex (
-point-vortex (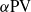 ) system, whose evolution corresponds to a unique global weak solution of the two-dimensional Euler-
) system, whose evolution corresponds to a unique global weak solution of the two-dimensional Euler- equations in the sense of distributions (Oliver & Shkoller, Commun. Part. Diff. Equ., vol. 26, 2001, pp. 295–314). Since the
equations in the sense of distributions (Oliver & Shkoller, Commun. Part. Diff. Equ., vol. 26, 2001, pp. 295–314). Since the 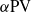 system is a formal regularization of the point-vortex system and it is known that, under a certain special condition, three point vortices collapse self-similarly in finite time (Kimura, J. Phys. Soc. Japan, vol. 56, 1987, pp. 2024–2030), we expect that the evolution of three
system is a formal regularization of the point-vortex system and it is known that, under a certain special condition, three point vortices collapse self-similarly in finite time (Kimura, J. Phys. Soc. Japan, vol. 56, 1987, pp. 2024–2030), we expect that the evolution of three  -point vortices for the same condition converges to a singular weak solution of the Euler-
-point vortices for the same condition converges to a singular weak solution of the Euler- equations that is close to the triple collapse as
equations that is close to the triple collapse as 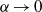 , which is examined in the paper. As a result, we find that the three
, which is examined in the paper. As a result, we find that the three  -point vortices collapse to a point and then expand to infinity self-similarly beyond the critical time in the limit. We also show that the Hamiltonian energy and a kinematic energy acquire a finite jump discontinuity at the critical time, but the energy dissipation rate converges to zero in the sense of distributions. On the other hand, an enstrophy variation converges to the
-point vortices collapse to a point and then expand to infinity self-similarly beyond the critical time in the limit. We also show that the Hamiltonian energy and a kinematic energy acquire a finite jump discontinuity at the critical time, but the energy dissipation rate converges to zero in the sense of distributions. On the other hand, an enstrophy variation converges to the 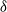 measure with a negative mass, which indicates that the enstrophy dissipates in the distributional sense via the self-similar triple collapse. Moreover, even if the special condition is perturbed, we can confirm numerically the convergence to the singular self-similar evolution with the enstrophy dissipation. This indicates that the self-similar triple collapse is a robust mechanism of the anomalous enstrophy dissipation in the sense that it is observed for a certain range of the parameter region.
measure with a negative mass, which indicates that the enstrophy dissipates in the distributional sense via the self-similar triple collapse. Moreover, even if the special condition is perturbed, we can confirm numerically the convergence to the singular self-similar evolution with the enstrophy dissipation. This indicates that the self-similar triple collapse is a robust mechanism of the anomalous enstrophy dissipation in the sense that it is observed for a certain range of the parameter region.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2012
References
- 12
- Cited by


