Instability of a dusty shear flow

Abstract

We study the instability of a dusty simple shear flow where the dust particles are distributed non-uniformly. A simple shear flow is modally stable to infinitesimal perturbations. Also, a band of particles remains unaffected in the absence of any background flow. However, we demonstrate that the combined scenario – comprising a simple shear flow with a localized band of particles – can exhibit destabilization due to their two-way interaction. The instability originates solely from the momentum feedback from the particle phase to the fluid phase. Eulerian–Lagrangian simulations are employed to illustrate the existence of this instability. Furthermore, the results are compared with a linear stability analysis of the system using an Eulerian–Eulerian model. Our findings indicate that the instability has an inviscid origin and is characterized by a critical wavelength below which it is not persistent. We have observed that increasing particle inertia dampens the unstable modes, whereas the strength of the instability increases with the strength of the coupling between the fluid and particle phases.

1. Introduction

Particle-laden flows are prevalent in various environmental, astrophysical and industrial settings. In the environmental context, these flows play pivotal roles in shaping the landscape around us through sediment transport (Burns & Meiburg 2015), influencing weather patterns via clouds (Pruppacher & Klett 1998; Shaw 2003), sea spray (Veron 2015), volcanic eruptions (Bercovici & Michaut 2010) and gravity currents (Necker et al. 2005). Astrophysical scenarios include particle-laden flows in cosmic dust clouds, stellar winds and the transport of interstellar dust particles in accretion disks and protoplanetary disks, which are crucial for forming and evolving planetary systems (Youdin & Goodman 2005; Fu et al. 2014; Homann et al. 2016). In industrial and engineering applications, particle-laden flows arise in processes like spray drying (Straatsma et al. 1999; Birchal et al. 2006), powder handling (Baxter et al. 2000) and fluidized bed reactors (Bi et al. 2000). Particle-laden flows typically involve multiple components, with at least a carrier phase and a dispersed phase, leading to physics occurring at multiple scales. In natural scenarios, the carrier flows are often turbulent, and the suspended particles are advected and sheared by this turbulence. Modelling particle-laden flows within a sufficiently dilute limit often involves considering the momentum exchange from the fluid to the particles while neglecting feedback from particles to the fluid (one-way coupling). However, this feedback is significant, especially when the mass fraction of particles to fluid is of the order of unity (e.g. dusty gas flows or water droplets in the air), as it can introduce new dynamics into the system. In this study we investigate a novel instability in a particle-laden simple shear flow arising from two-way coupling, where the feedback force from particles to fluid is considered.

The non-uniform distribution of particles, also known as particle segregation or particle banding, is observed in particle-laden flows across diverse engineering and environmental contexts. It can occur due to various segregation mechanisms such as preferential clustering, differential settling velocities, turbulent dispersion and particle–particle interactions. For example, in turbulent flows, inertial particles can cluster preferentially in regions of high strain and lower vorticity, forming regions with high and low particle concentration (Maxey 1987; Bec 2005; Fiabane et al. 2012). This phenomenon can arise solely from one-way coupling, and no feedback force is required. In pneumatic conveying systems transporting granular materials, such as powders or grains, bands of particle-rich and particle-deficient regions can form (known as rope formation) due to agglomeration and flow dynamics (Huber & Sommerfeld 1994; Klinzing et al. 2011; Laín & Sommerfeld 2013; Zhang et al. 2023). In turbulent wall-bounded flows carrying suspended particles, such as industrial pipelines transporting slurries, particle segregation can occur due to differential settling velocities, turbulent dispersion and thermophoresis. This segregation can lead to the formation of particle-rich layers near the bottom or walls of the flow channel, with particle-deficient regions in the core of the flow (Marchioli et al. 2003; Picano, Sardina & Casciola 2009; Sardina et al. 2012). The particles form extremely long clusters, called ropes, and align preferentially with the low-speed turbulent streaks, contributing to their stabilization and suppression of bursting (Dave & Kasbaoui 2023). Despite the additional stresses resulting from particles, the alteration of near-wall coherent structures results in a notable decrease in Reynolds shear stresses and partial relaminarization of the near-wall flow. Fluidized bed reactors used in chemical engineering often exhibit particle banding phenomena (Harris & Crighton 1994; Gilbertson & Eames 2001; Liu et al. 2016). Observations of sediment-laden river flows and estuarine environments have revealed the formation of bands of sediment deposition influenced by flow dynamics, sediment transport mechanisms, coagulation and channel morphology (Gibbs 1986; Sondi, Juračić & Pravdić 1995; Ogami, Sugai & Fujiwara 2015). These sediment bands play a crucial role in shaping riverbeds, deltas and coastal environments.

In astrophysical accretion disks, such as those around young stars or black holes, there are regions where gas and dust particles orbit around a central object. The dust–gas system exhibits Keplerian motion, alongside radial and azimuthal drifts between the dust and gas. When the gas and dust move at slightly different velocities, this disparity can result in a relative drift between the two components. This relative motion creates a shearing force that can amplify small perturbations/disturbances in the dust distribution – known as streaming instability (Youdin & Goodman 2005; Chiang & Youdin 2010). The name ‘streaming instability’ reflects the differential streaming motion between gas and dust particles within the disk. The instability arises from the relative drift between the gas and dust phases, a universal consequence of radial pressure gradients. Growth occurs even though the two components interact only via dissipative drag forces. Streaming instability exhibits growth rates that are slower than dynamical time scales but faster than drift time scales. As a result, dust particles start clumping together, even without self-gravity, forming dense structures or bands. Thus, the dust particles can localize, leading to additional dynamics or instabilities due to the Keplerian shear (as we see in this paper) and self-gravity. Thus, streaming instability is crucial in various astrophysical processes, including planetesimals’ formation and dust grains’ growth in protoplanetary disks.

The hydrodynamic stability characteristics of particle-laden flows can be altered by modifying existing instabilities or generating new types of instabilities, as one considers the feedback from particles. Early studies by Kazakevich & Krapivin (1958) and Sproull (1961) observed a notable reduction in the resistance coefficient when dust was added to the air flowing turbulently through a pipe. It was thought that adding particles altered the effective viscosity that led to this modification; however, this contradicts Einstein's formula for the suspension viscosity. Saffman (1962) was among the first to provide an analytical model for studying the stability of a dusty planar flow. Saffman proposed that inertial particles extract energy from turbulent fluctuations, thereby damping them. Using a two-fluid model, Saffman modelled both particle and fluid phases as a continuum. The momentum exchange between both phases is accounted for using a linear Stokes drag. The modal analysis ultimately resulted in a modified Orr–Sommerfeld equation for uniformly distributed particles. Saffman (1962) deduced that finer particles with low inertia could induce destabilization due to a reduction in effective kinematic viscosity. Although the effect of particles on the viscosity of dusty gas is negligible, it effectively increases the gas density, thereby reducing the kinematic viscosity. Conversely, coarser particles with high inertia could lead to stabilization through dissipation by Stokes drag. Saffman concluded that dust merely alters the waves present in a clean gas and may not introduce any additional instabilities. Subsequent studies have numerically solved the modified Orr–Sommerfeld equation for various base flows, confirming Saffman's conclusions (Michael 1964; Asmolov & Manuilovich 1998; Tong & Wang 1999; Klinkenberg, De Lange & Brandt 2011; Sozza et al. 2022). Sozza et al. (2020, 2022) investigated a dusty Kolmogorov flow and demonstrated that increasing the particle mass loading reduces the amplitude of the mean flow and turbulence intensity. They observed that turbulence suppression is more pronounced for particles with smaller inertia. The study concluded that while inertia significantly influences particle dynamics, its impact on flow properties is negligible compared with mass loading.

Notably, Saffman's analysis does not account for gravitational effects. Including gravity can introduce buoyancy effects that may destabilize the flow more easily (Herbolzheimer 1983; Shaqfeh & Acrivos 1986; Borhan & Acrivos 1988). For example, Magnani, Musacchio & Boffetta (2021) investigated dusty Rayleigh–Taylor turbulence and found that the interface between the two phases becomes unstable in the presence of gravity forces, evolving into a turbulent mixing layer that broadens over time. However, in a particle-laden Rayleigh–Bénard system (Prakhar & Prosperetti 2021), it was observed that particles tend to inhibit the onset of natural convection, thereby stabilizing the system. This is because particles act as a distributed drag force and heat source in the fluid, similar to a porous medium. Saffman's analysis, also, focusing solely on uniform particle distribution, overlooks the potential effects of non-uniform distributions. A study by Narayanan & Lakehal (2002) has demonstrated the presence of additional unstable modes under large Stokes numbers and high mass loading conditions in a particle-laden mixing layer where the particle distribution is localized. Additionally, investigations utilizing non-uniform particle distributions have highlighted the emergence of novel instabilities (Senatore, Davis & Jacobs 2015; Warrier, Hemchandra & Tomar 2023).

The non-uniform distribution of inertial particles arises naturally in vortical flows due to their preferential accumulation. As noted earlier, it has long been recognized that inertial particles tend to be centrifuged from vortical regions and cluster in regions of high strain (Maxey 1987), a phenomenon known as preferential accumulation. A numerical investigation by Shuai & Kasbaoui (2022) demonstrated that in a Lamb–Oseen vortex, inertial particles are expelled from the vortex core, forming a ring-shaped cluster and a void fraction bubble that expands outward. However, without accounting for the two-way interaction, the vortex would decay slowly due to viscous dissipation. When the two-way coupling is considered, it is observed that the feedback from clustered particles flattens the vorticity distribution and leads to an accelerated vortex decay. It is noted that as the inertia of the particles increases, the vorticity decays even more rapidly. A follow-up numerical study by Shuai et al. (2022) on a particle-laden Rankine vortex revealed that the system becomes unstable due to the two-way interaction, which is also validated by analytical linear stability analysis (LSA). The feedback force from the particles triggers a novel instability, which can cause the breakdown of an otherwise resilient vortical structure. In the context of the merging of a pair of co-rotating vortices laden with inertial particles, it has been shown (Shuai, Roy & Kasbaoui 2024) that the feedback force from particles significantly alters the monotonic merging behaviour as observed without feedback. The vortices push apart for a while due to a net repulsive force from particles ejected from the vortex cores, thus delaying their merging.

Apart from modal instability, the interplay between particle inertia and shear from the base flow can lead to transient growth of perturbations in particle-laden flows via non-modal growth mechanisms such as the Orr mechanism or the ‘lift-up’ effect. Performing a non-modal analysis, Klinkenberg et al. (2011) showed that transient growth in a particle-laden channel flow increases proportionally with the particle mass fraction. Similar non-modal instabilities have been observed and studied in dusty gas flows, such as the Blasius boundary layer with a localized dust layer (Boronin & Osiptsov 2014), plane channel suspension flow with a Gaussian layer of particles (Boronin & Osiptsov 2016) and stably stratified Blasius boundary layer flow (Parente et al. 2020). Additionally, the inclusion of gravitational effects in a simple shear flow has been shown to alter the uniformity of particle distribution, leading to the formation of local particle clusters and, subsequently, to transient growth (Kasbaoui et al. 2015).

The previously mentioned studies mostly used an Eulerian–Eulerian model for particle-laden flows. However, there are three primary methods for modelling particle-laden flows: (i) Eulerian–Eulerian modelling, (ii) Eulerian–Lagrangian (EL) modelling and (iii) fully resolved simulations. The Eulerian–Eulerian method (see Jackson 2000; Drew & Passman 2006) treats both the particle and fluid phases as interpenetrating continua in an Eulerian framework, assuming particles are small ($\Delta x \gg d_p$) and sufficiently densely distributed to be treated as a fluid continuum. While computationally more affordable, this method may introduce errors due to the difficulty of modelling terms in Eulerian–Eulerian methods that require closure. In contrast, the EL method treats the fluid phase as a continuum within an Eulerian framework while representing the particle phase as discrete entities tracked individually in a Lagrangian manner. Here, the fluid phase is solved at a coarser scale, typically with $\Delta x$ a few times larger than $d_p$, resulting in a scalable and cost-effective approach. However, empirical coupling between the particle and fluid phases introduces some approximation errors. A few studies that considered EL modelling and the stability of particle-laden flows are Meiburg et al. (2000), Richter & Sullivan (2013), Senatore et al. (2015), Kasbaoui et al. (2015), Wang & Richter (2019), Kasbaoui (2019), Pandey, Perlekar & Mitra (2019) and Shuai et al. (2022). The fully resolved method, for example, realized by the immersed boundary method (see Uhlmann 2005; Breugem 2012; Kempe & Fröhlich 2012; Dave, Herrmann & Kasbaoui 2023; Kasbaoui & Herrmann 2024), is employed when the grid spacing $\Delta x$ is significantly smaller than the particle diameter $d_p$. While offering high accuracy, this method requires extensive resolution, making it costly and impractical for large-scale applications. Thus, in this study we only employ the EL and Eulerian–Eulerian methods, the details of which are discussed respectively in §§ 2.1 and 4.1.

Here, we investigate the stability of a dusty simple shear flow with non-uniformly distributed particles. This configuration is an idealized set-up for natural phenomena such as sea-spray dynamics at the ocean–atmosphere interface (Barenblatt, Chorin & Prostokishin 2005; Veron 2015), particle rope formation in pneumatic conveying (Kruggel-Emden & Oschmann 2014) and dust particles in planetary accretion disks (Youdin & Goodman 2005). These scenarios involve inertial particles that are locally concentrated in a background shear flow (e.g. a turbulent shear boundary layer or Keplerian shear). At the leading order, the system can be approximated by a top-hat distribution of particle concentration in a simple shear flow. In the absence of particles, a simple shear flow is modally stable to infinitesimal perturbations. Similarly, a non-uniform particle distribution without any background flow remains unaffected. Thus, each system under consideration is linearly stable when inspected in isolation. However, when considering the combined system (see the schematic in figure 1), where a simple shear flow is superimposed on a band of particles, the background flow advects the particles, and the feedback from the particles induces an instability in the system. This study reveals that this seemingly simple yet crucial particle-laden system exhibits a novel type of instability when incorporating two-way coupling. In § 2 we demonstrate the presence of this novel instability through EL numerical simulations. The mechanism underlying the genesis of this new instability is described in § 3. An analytical study of the system is carried out in § 4 using an Eulerian–Eulerian framework. Following the approach of Saffman (1962), LSA is employed to establish the existence and modal nature of the instability. Section 5 offers a comparative analysis between the EL and Eulerian–Eulerian results. Finally, we conclude in § 6.

Figure 1. Schematic showing the configuration studied here: (a) an unbounded simple shear flow (with a shear rate $\varGamma > 0$) passing over a band of particles. The particles of uniform size are randomly distributed within a band of width $h$ with equal probability, forming a top-hat distribution of particle number density ($N(y)$), as shown in (b).

2. Evidence of instability in a two-way coupled particle-laden shear flow

In this section we present a novel instability occurring in a particle-laden simple shear flow. Along with the momentum transport from the fluid to particle phase, we consider the feedback from the particle to fluid phase (two-way coupling), which is crucial for the instability to occur. We employ an EL method to illustrate this instability. Below, we describe the method used.

2.1. Eulerian–Lagrangian method

The EL simulations presented here are based on the volume-filtered (VF) formulation (Anderson & Jackson 1967; Jackson 2000; Capecelatro & Desjardins 2013). In the EL formulation the fluid phase is treated in the Eulerian frame as a continuum, while the particle phase is treated in the Lagrangian frame, with discrete particles tracked individually.

The VF conservation equations govern the fluid (carrier) phase in the semi-dilute regime (low particle volume fraction) as

(2.1a)\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u} =0, \end{gather}

(2.1b)\begin{gather}\rho_f \left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}\right) ={-}\boldsymbol{\nabla}p+\mu_f \nabla^2\boldsymbol{u}+\boldsymbol{F}_p, \end{gather}

where $\boldsymbol {u}$ is the VF fluid velocity, $p$ is the VF pressure, $\rho _f$ is the fluid density and $\mu _f$ is the fluid viscosity. The term $\boldsymbol {F}_p$ represents momentum exchange from particles (dispersed phase) to fluid. For a semi-dilute concentration of particles ($\phi _p \ll 1$), $\boldsymbol {F}_p$ can be expressed as

(2.2)\begin{equation} \boldsymbol{F}_p ={-}\phi_p \left. \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{\tau}\right|_p+\rho_p \phi_p \frac{(\boldsymbol{v}- \boldsymbol{u}|_p)}{\tau_p}, \end{equation}

where $\rho _p$ is the particle density, $\phi _p$ represents the volume fraction of particles in the fluid medium, $\tau _p = \rho _p d_p^2/(18 \mu _f)$ is the relaxation time scale of the particle to the fluid acceleration and $d_p$ the particle diameter. The total fluid stress, denoted as $\boldsymbol {\tau }$, is determined from the combination of pressure and viscous stresses as $-p\boldsymbol {I} + \mu _f (\boldsymbol {\nabla } \boldsymbol {u}+\boldsymbol {\nabla }\boldsymbol {u}^{\textrm {T}})$, where $\boldsymbol {\nabla } \boldsymbol {u}$ represents the fluid velocity gradient, $\boldsymbol {I}$ is the identity matrix and $({\cdot })^{\textrm {T}}$ is the transpose operator. The Eulerian particle velocity, $\boldsymbol {v}$, is computed from Lagrangian particle velocities using (2.4). The notation $({\cdot }) |_p$ specifies fluid properties evaluated at the locations of the particles. The fluid velocity at the particle location ($\boldsymbol {u}|_p$) is obtained through a trilinear interpolation, as described in Capecelatro & Desjardins (2013). In (2.2) the first term represents the stress exerted by the undisturbed flow at the location of the particle. The next term accounts for stresses induced by the presence of particles, characterized by Stokes drag, for $Re_p \ll 1$, where $Re_p$ is the Reynolds number based on particle size. The Stokes drag must be evaluated using the slip velocity between the particle and the undisturbed fluid. In situations where the density ratio ($\rho _p/\rho _f$) is significantly higher (e.g. dusty gas flows, water droplets in the air), as in our study, Stokes drag dominates the momentum exchange. Since the density ratio is very large and the particle volume fraction is very low, the first term in (2.2) is negligible compared with the second term. Although our EL simulation implementation generally accounts for both of these terms, we will later see in § 4 that, in the LSA, only the Stokes drag term is used, and the first term is neglected for simplicity.

The particles are tracked in a Lagrangian sense. Assuming point spherical particles in a $Re_p \ll 1$ flow regime, the dynamic equation for ${i}{\rm th}$ particle is given by Maxey & Riley (1983) as

(2.3)\begin{equation} \frac{{\rm d}\boldsymbol{v}^i}{{\rm d} t} = \frac{1}{\rho_p} \left. \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{\tau}\right|_p+\frac{\left. \boldsymbol{u}\right|_p-\boldsymbol{v}^i}{\tau_p},\quad \textrm{with} \ \frac{{\rm d}{\kern0.9pt}\boldsymbol{x}^i}{{\rm d}t} = \boldsymbol{v}^i, \end{equation}

where $\boldsymbol {x}^i$ and $\boldsymbol {v}^i$ are the position and velocity of the ${i}{\rm th}$ particle, respectively. In this study, gravitational/sedimentation effects have been omitted to isolate and comprehend the distinctive impact of two-way coupling on instability. Also, we operate in the semi-dilute regime to avoid any potential particle–particle interactions such as collision. Also, as mentioned earlier, the density ratio ($\rho _p/\rho _f$) is kept large, so the added mass effect, Basset history force and Saffman lift force are negligible. To evaluate the momentum feedback from the particle phase to the fluid phase ($\boldsymbol {F}_p$), one needs to evaluate the instantaneous particle volume fraction and Eulerian particle velocity field. At a location $\boldsymbol {r}$, these are obtained from the corresponding instantaneous Lagrangian quantities using

(2.4a)\begin{gather} \phi_p(\boldsymbol{r}) = \sum_{i = 1}^{N}V_p g(\lVert \boldsymbol{r}-\boldsymbol{x}^i\rVert), \end{gather}

(2.4b)\begin{gather}\phi_p(\boldsymbol{r}) \boldsymbol{v}(\boldsymbol{r}) = \sum_{i = 1}^{N}\boldsymbol{v}^iV_p g(\lVert \boldsymbol{r}-\boldsymbol{x}^i\rVert), \end{gather}

where $V_p = {\rm \pi}d_p^3/6$ is the particle volume, $g$ represents a Gaussian filter kernel of size $\delta _f = 3 \Delta x$, where $\Delta x$ is the grid spacing (Capecelatro & Desjardins 2013). In the VF method the Gaussian kernel smoothes out/regularizes the fluctuations in momentum feedback, thereby preventing any convergence issues during simulation. The VF model was recently applied by the authors successfully in particle-laden vortical flows (Shuai & Kasbaoui 2022; Shuai et al. 2022, 2024). Readers interested in further details about the numerical approach may refer to them.

The Reynolds stress term, or the subgrid-scale tensor, is an important consideration during the filtering operation. In a multiphase flow like ours, this term can arise from (i) turbulent fluctuations in the fluid phase and (ii) fluctuations created by the particles. Since our simulations are not in the turbulent regime, the first contribution can be readily neglected. As for the contribution due to particle disturbances, it is not clear whether it is significant and how to model it. There are ongoing efforts to model the particle-induced subfilter-scale tensor, such as the recent work by Hausmann, Evrard & van Wachem (2023). However, due to the large modelling uncertainty, there is no clear consensus on how to model these subfilter effects. These considerations are outside the scope of this paper, and thus, we neglect subfilter-scale effects other than those that appear in the feedback force in our analysis.

The works of Sundaram & Collins (1996) and Peskin (2002) demonstrated that, in EL simulations, using different schemes for interpolating fluid velocity at particle positions and for extrapolating particle feedback forces to the fluid phase can result in an error gap in the kinetic energy budget. However, this issue pertains specifically to point-particle models, where discrete Dirac delta functions acting on the Navier–Stokes equations represent the particle feedback force. Our method, by contrast, follows a VF approach, as outlined by Capecelatro & Desjardins (2013), where the governing equations are derived via convolution with a smooth kernel, such as a Gaussian. A comparison of both methods with experimental results for the case of a particle-laden vertical turbulent channel flow can be found in Wang et al. (2019). Given the fundamental differences in our approach, the kinetic energy gap highlighted by Sundaram & Collins (1996) does not apply to our simulations despite using trilinear interpolation for fluid velocity at particle positions and a Gaussian kernel for particle feedback. While we are unaware of any hidden energy imbalance, this falls beyond the scope of the present study. Furthermore, Ireland & Desjardins (2017) demonstrated that applying additional corrections to the fluid velocity at particle positions did not lead to statistically significant variations in time-averaged quantities, such as fluctuation energy or fluid kinetic energy.

In (2.2) and (2.3), when evaluating the drag term, the fluid velocity at the particle location, $\boldsymbol {u}|_p$, should ideally represent the undisturbed flow. However, since the simulation accounts for the presence of particles, the fluid velocity is already disturbed, making it challenging to accurately estimate the undisturbed flow velocity. This error can lead to unphysical, self-induced particle motion, which is a known challenge in EL simulations. The self-induced motion is influenced by the length scale of the interpolation kernel $g$. Studies such as Ireland & Desjardins (2017) and Balachandar, Liu & Lakhote (2019) have proposed corrections for estimating $\boldsymbol {u}|_p$, to reduce the risk of this unphysical phenomenon. These studies suggest that the correction for self-induced velocity is proportional to the ratio of particle diameter to filter width, $d_p/\delta _f$. To minimize the effect, one must maintain $d_p/\delta _f \ll 1$, ensuring that the kernel's length scale is large enough and that many particles lie within the volume occupied by the kernel. Consequently, the flow is modified by the collective effect of many particles, making the individual self-induced motion negligible.

A scaling analysis of the drag force in (2.2) reveals the coupling strength of feedback force from particle phase to fluid phase is governed by the non-dimensional number $M = \rho _p \langle \phi _p \rangle /\rho _f$ – the mass loading (or mass fraction), where $\langle \phi _p \rangle$ is the average volume fraction of particles. If the particle field is dilute and the mass loading is negligible, the feedback force can be neglected, and the one-way coupled simulations can be used to describe the evolution of the particulate flow. However, when the density ratio ($\rho _p/\rho _f$) is significant, as is the case here, the mass loading becomes ${O}(1)$, which leads to significant feedback to the fluid phase from the particle phase, even if the particle phase is dilute (Kasbaoui et al. 2015). As we will see in the upcoming sections, this feedback is the source of instability in the present study, as the system considered here is stable under one-way coupling.

2.2. Illustration of the instability

To demonstrate the instability resulting from two-way coupling, we investigate an unbounded simple shear flow combined with a band of particles distributed in a top-hat manner (refer to the schematic in figure 1). The fluid properties include a density of $\rho _f = 1.0 \ \textrm {Kg}\ \textrm {m}^{-3}$, viscosity of $\mu _f = 1.5\times 10^{-5}\ \textrm {Kg}\ \textrm {m}^{-1}\ \textrm {s}^{-1}$ and a flow shear rate of $\varGamma = 12.65\ \textrm {s}^{-1}$. The particles are monodisperse with a diameter $d_p = 4.62 \ \mathrm {\mu } \textrm {m}$ and density $\rho _p = 1000\ \textrm {Kg}\ \textrm {m}^{-3}$, distributed uniformly within a region $\lvert y \rvert \leqslant h/2$. The band width is chosen as $h = 6\ \textrm {mm}$ to maintain a large $h/d_p$ ratio, approximately $h/d_p \approx 1300$, ensuring that the fluctuations caused by discrete particle forcing remain well below the viscous dissipation scale. The average volume fraction of particles within the band is set to $\langle \phi _p \rangle = 10^{-3}$. In terms of non-dimensional numbers, this corresponds to a density ratio of $\rho _p/\rho _f = 1000$, Stokes number $St =\varGamma \tau _p= 10^{-3}$ and mass loading $M = (\rho _p/\rho _f) \langle \phi _p \rangle = 1$, which is significant. Here, $\tau _p = \rho _p d_p^2/(18 \mu _f)$ is the particle relaxation time.

The relative importance of the gravitational settling speed ($V_s = g \tau _p$) of particles compared with the characteristic flow speed ($V_c = \varGamma h$) can be evaluated as $V_s/V_c = St/Fr^2 \approx 0.01$. Here, $g$ is the acceleration due to gravity and $Fr = V_c/\sqrt {g h}$ is the Froude number, a dimensionless number that measures the relative importance of inertial forces to gravitational forces. Given that the ratio $V_s/V_c$ is very small, it is evident that the gravitational settling effect of particles is negligible in this set-up. Consequently, we have ignored it in our study. Furthermore, the Saffman lift force (Saffman 1965) experienced by a particle moving in a simple shear flow is given by $\boldsymbol {L} = 1.615 \mu _f d_p \lvert \boldsymbol {u}_s\rvert \, \sqrt {d_p^2 \lvert \boldsymbol {\omega }\rvert \rho _f/\mu _f}\, (\boldsymbol {\omega } \times \boldsymbol {u}_s)/(\lvert \boldsymbol {\omega }\rvert \, \lvert \boldsymbol {u}_s\rvert )$ (see Candelier et al. (2023) for a generalization of inertial forces in linear flows, accounting for transient effects). When compared with the Stokes drag $\boldsymbol {D} = 3 {\rm \pi}\mu _f d_p \boldsymbol {u}_s$, this yields $\lvert \boldsymbol {L}\rvert /\lvert \boldsymbol {D}\rvert \sim (1.615/{\rm \pi} )\, \sqrt {2 \,St\, \rho _f/\rho _p} \simeq 7.27 \times 10^{-4}$. Here, $\boldsymbol {u}_s$ is the slip velocity between the particle and the fluid, and $\boldsymbol {\omega }$ is the vorticity at the particle location, assumed to scale with the background shear rate as $\lvert \boldsymbol {\omega }\rvert \sim \varGamma$. The negligible ratio of lift to drag force allows us to ignore the lift force in this study, as reflected in (2.3).

The numerical simulation is performed in a box of dimensions $L_x\times L_y\times L_z$, where $L_x \approx 16\,666 d_p$, $L_y = 3 L_x$ and $L_z = 3 d_p$. To avoid unwanted diffusion effects, the Reynolds number based on the box width is thus set to $Re_{L_x} = \varGamma L_x^2\rho _f/\mu _f \approx 5000$, and we focus on inviscid instability. The flow needs to be periodic in the $x$ direction and unbounded in the $y$ direction. To achieve this within the simulation box, we apply regular periodic boundary conditions at the left and right boundaries (in the $x$ direction) and shear-periodic boundary conditions at the top and bottom boundaries (in the $y$ direction), accounting for the background shear flow (see Kasbaoui et al. 2017). By choosing a domain size that is three times larger in the $y$ direction, we ensure neighbouring periodic simulation boxes are well separated and do not interfere with each other to influence the instability. We use the EL framework described above on a uniform Cartesian grid with resolution $h/\Delta x \approx 41$, $N_x = 512$, $N_y = 3 N_x$ and $N_z = 1$. The ratio $d_p/\delta _f$ is maintained at approximately $0.01$, a sufficiently small value, ensuring that the self-induced motion of particles is negligible. Here, we perform pseudo-two-dimensional simulations by considering only one grid point in the axial ($z$) direction with periodic boundary conditions applied over a thickness $\Delta z = 3 d_p$. This allows the definition of volumetric quantities such as particle volume and volume fraction.

In addition to conducting two-way coupled simulations, we perform one-way coupled simulations, where the momentum exchange term (2.2) is neglected. The particles still evolve due to the momentum contribution from the fluid. However, the particles’ feedback to the fluid phase is deliberately switched off. This allows for comparison between one-way and two-way coupled simulations and showcases the impact of particle feedback on the flow dynamics.

The fluid velocity field is initially superimposed with a two-dimensional incompressible perturbation of the form $\tilde {u}_x = \epsilon \varGamma h\,{\rm e}^{-y^2/\beta ^2}\, (2y/k \beta ^2)\sin k x$ and $\tilde {u}_y = \epsilon \varGamma h\, {\rm e}^{-y^2/\beta ^2} \cos k x$. The perturbation has an amplitude of $\epsilon = 10^{-2}$ relative to the characteristic flow velocity $\varGamma h$, where, as mentioned earlier, $\varGamma = 12.65\ \textrm {s}^{-1}$ and $h = 6\ \textrm {mm}$. It features a sinusoidal variation in the $x$ direction, set to contain four full periods in the domain, i.e. $\lambda = L_x/4$, where $\lambda$ is the wavelength of the perturbation in the $x$ direction (i.e. $k h = 2$ with dimensional wave number $k = 2{\rm \pi} /\lambda$). The perturbation decays in the $y$ direction in a Gaussian manner with a characteristic width $\beta = 2 h$. The corresponding perturbation vorticity field is shown in figure 2, at $\varGamma t = 0$. The initial velocity of the particles is set equal to the local fluid velocity.

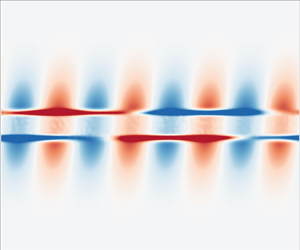
Figure 2. The time evolution of isocontours of normalized perturbation vorticity ($\tilde {q}_z/\tilde {q}_0$) for two-way coupling (a–e) and one-way coupling (f–j) is shown. The corresponding simulation parameters are set to $M=1$, $St = 10^{-3}$, $\epsilon = 10^{-2}$ and $\langle \phi _p \rangle = 10^{-3}$. For better visualization, the figures are zoomed in and cropped to centre the view on the particle band, although the simulation domain is larger, especially in the $y$ direction. In addition, the coordinates in both directions are scaled with the band width $h$.

The evolution of the vorticity perturbation $\tilde {q}_z$ normalized by its initial maximum value $\tilde {q}_0 = \epsilon \varGamma h\, (k+2/(k \beta ^2)) = (9/4) \epsilon \varGamma$ is presented in figure 2. Successive snapshots are provided for various non-dimensional times $\varGamma t = 0, 0.1, 1, 2$ and $3$. The snapshots are confined to a domain that is zoomed in and cropped around the particle band for better visualization, although the simulations use a larger domain size, especially in the $y$ direction, as mentioned earlier. In the case of one-way coupling (f–j), it is observed that the vorticity patches are sheared, tilted and stretched by the background flow, and the intensity of vorticity diminishes as time progresses. The downstream tilt of the vorticity perturbations and the related algebraic decay of associated perturbation energy by the Orr mechanism are described in detail in Farrell (1987) and Roy & Subramanian (2014). The perturbed flow had a periodic behaviour with a wavelength in the $x$ direction of $\lambda = L_x/4$, which remains unchanged as time advances. At later times, it can be seen that the perturbation field eventually decays.

Conversely, when considering two-way coupling (a–e), we observe significant evolution and amplification of the vorticity field. The initially perturbed mode with $\lambda = L_x/4$ disappears, giving way to a new mode with $\lambda = L_x$. These newly emerged structures, likely unstable eigenmodes, persist and their corresponding vorticity field intensifies over time. As the simulation progresses, nonlinear interactions between successive vorticity patches become more pronounced, eventually leading to a transition into a strongly nonlinear regime (not shown here).

Particle dispersion is also significantly affected when two-way coupling is considered. Figure 3 depicts the evolution of the particle volume fraction field scaled with the average initial volume fraction. When the particle feedback is neglected (f–j), the shear flow simply advects the particles. As the flow perturbations decay over time, they have minimal impact on particle transport, even after a significantly longer duration. Eventually, the disturbances die out and the particle distribution resembles the initial band (see figure 3(f–j) at $\varGamma t = 0$ and $25$). In contrast, two-way coupling leads to growing flow perturbations, which in turn govern the dispersion of particles (a–e). Initially, the uniform particle band undergoes deformation due to flow disturbances characterized by a periodic mode of $\lambda = L_x$. As time progresses, the interplay between background shear flow and growing perturbations initiates nonlinear effects, resulting in particle clustering into lobes interconnected by a relatively slender filament, as can be seen in figure 3(a–e), at $\varGamma t=25$.

Figure 3. The time evolution of isocontours of the normalized particle number density ($n = \phi _p/\langle \phi _p \rangle$), corresponding to the simulation in figure 2, is shown. The large time snapshots illustrate the nonlinear evolution of the instability in the two-way coupling case.

The simulations shown in figures 2 and 3 suggest that semi-dilute inertial particles, distributed non-uniformly in an unbounded simple shear flow, can induce hydrodynamic instability. This instability cannot be solely attributed to hydrodynamics since the simple shear flow in a single-phase flow is stable to infinitesimal perturbations (see Drazin & Reid 2004). Furthermore, it cannot be attributed to collisional effects, as the simulation neglected particle–particle interactions. Instead, the instability must arise from the two-way momentum exchange between the two phases, as confirmed by the absence of instability when the two-way coupling term is deactivated in the simulation. Previous studies have shown that uniformly distributed particles in a simple shear flow, even with two-way coupling, do not exhibit modal instability but can demonstrate only a non-modal instability if gravitational effects are considered (Kasbaoui et al. 2015). However, in this study we observe the emergence of a new type of instability resulting from the interaction between the simple shear flow and a non-uniformly distributed particle field in the absence of gravitational settling. In the subsequent sections we demonstrate that this new type of instability is modal and explain its generation mechanism. The following section will provide a mechanistic explanation of the instability through wave interactions.

3. Mechanism of instability: a dusty Taylor–Caulfield instability

In the previous section we observed that instability arises from the two-way coupling between the particle and fluid phases, driven by the finite inertia of the particles. Surprisingly, even weakly inertial particles ($St = 10^{-3}$) triggered the instability. In this section we delve into the instability mechanism in the small particle inertia limit while still considering the particle–fluid coupling. We employ the concept of wave interaction to elucidate this instability mechanism. In the weak particle inertia limit we demonstrate that our particle-laden system resembles a stratified fluid system. The fluid exhibits an effective modified density, which is stratified due to the particle concentration gradient. This density stratification creates edge waves and their interaction leads to instability, similar to the case of the Taylor–Caulfield instability (Taylor 1931; Caulfield 1994; Balmforth, Roy & Caulfield 2012). However, there is a caveat: the wave generation mechanism differs slightly here, which we will address as we proceed.

In the limit of weak particle inertia, following Ferry & Balachandar (2001), Rani & Balachandar (2003), the feedback force $\boldsymbol {F}_p$ in (2.2) for dusty gas system can be approximated as $\boldsymbol {F}_p = -\rho _p\phi _p \boldsymbol {a}+{O}(\tau _p)$, where $\boldsymbol {a} = ( \partial \boldsymbol {u}/\partial t+\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla }\boldsymbol {u})$ represents the fluid acceleration term. Substituting it back into (2.1b) yields a simplified form representing a fluid with modified density (in the inviscid limit) as

(3.1)\begin{equation} \rho \left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u}\right) ={-}\boldsymbol{\nabla}p, \end{equation}

where $\rho = \rho _f + \rho _p n \langle \phi _p \rangle$ represents an effective fluid density due to the suspended particles, where $n = \phi _p/\langle \phi _p \rangle$ is the normalized particle number density. Thus, a spatial inhomogeneity in the particle concentration can result in a variation in the effective density of this composite fluid even if $\rho _f$ is a constant. Additionally, the conservation of the total number of particles yields

(3.2)\begin{equation} \frac{\partial \rho}{\partial t}+\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla}\rho = 0. \end{equation}

Together, (2.1a), (3.1) and (3.2) resemble a stratified incompressible fluid system and is known as the single-fluid continuum model describing a particle-laden system. Taking the curl of (3.1) after scaling it with $\rho$ gives the evolution equation for the flow vorticity ($\boldsymbol {q} = \boldsymbol {\nabla } \times \boldsymbol {u}$) as (for a two-dimensional case)

(3.3)\begin{equation} \left(\frac{\partial \boldsymbol{q}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{q}\right) = \boldsymbol{a} \times\frac{\boldsymbol{\nabla} \rho}{\rho}, \end{equation}

where we have used the relation between $\boldsymbol {a}$ and $\boldsymbol {\nabla }p$ from (3.1) here for further simplification. A general evolution equation for vorticity in a multiphase flow is obtained by Osnes, Vartdal & Pettersson Reif (2018) by taking the curl of the momentum conservation equation for the fluid phase. According to the equation, in a two-dimensional, incompressible flow the vorticity generation is due to three factors: (i) barotropic torque, (ii) torque due to feedback force, and (iii) torque due to the misalignment between volume-fraction-weighted fluid density and feedback force. Out of these, the last two terms are present only because of the feedback force from particles. In the dilute limit of particle concentration and negligible particle inertia, one can approximate the feedback force as mentioned earlier, $\boldsymbol {F}_p \approx -\rho _p\phi _p \boldsymbol {a}$, and reduce Osnes's general multiphase vorticity equation to our (3.3), assuming no barotropic torque generation. According to Osnes's equation, vorticity is generated due to the particle feedback force, especially when the relative velocity between the particle and fluid phases remains large, and the particles remain accelerated or decelerated, as noted in the case of channelling instability (Koneru et al. 2020; Ouellet et al. 2022). When viewed in terms of (3.3), this indicates that vorticity can arise in the system due to the misalignment between fluid acceleration and the gradient in particle concentration due to the baroclinic source term $\boldsymbol {a} \times \boldsymbol {\nabla }\rho$. In the subsequent paragraphs we demonstrate the precise way by which vorticity is generated in our system and how it gives rise to propagating waves that can interact and lead to instability.

The base state flow may inherently possess a vorticity field. However, the additional vorticity disturbance created would be responsible for generating waves. To analyse this, we need to consider the evolution equation for the disturbance vorticity field. Without loss of generality, let us consider a general two-dimensional system in the $x$–$y$ plane with unidirectional flow in the horizontal direction and vertically stratified particle distribution. We can decompose the relevant quantities into base state and disturbance (denoted by $\widetilde {()}$) parts as $\boldsymbol {u} = U(y)\, \hat {\boldsymbol {x}} + \tilde {\boldsymbol {u}}(x,y)$ and $\rho = \rho _b(y) + \tilde {\rho }(x,y)$. The vorticity field $\boldsymbol {q}=q_z\, \hat {\boldsymbol {z}}$ will be along the $\hat {\boldsymbol {z}}$ direction and can be decomposed as $q_z = Q_z(y) + \tilde {q}_z(x,y)$, where the base state vorticity is $Q_z(y) = -U'(y)$. Substituting these expressions into (3.3) and considering the leading disturbance terms, we obtain the linearized evolution equation for the disturbance vorticity field as

(3.4)\begin{equation} \frac{\mathcal{D} \tilde{q}_z}{\mathcal{D} t} = \frac{\rho_b'}{\rho_b} \frac{\mathcal{D} \tilde{u}_x}{\mathcal{D} t}+\frac{(\rho_b U')'}{\rho_b}\, \tilde{u}_y, \end{equation}

where the operator $\mathcal {D}/\mathcal {D} t = \partial /\partial t+U(y) \partial /\partial x$ represents the linearized material derivative and $()'$ represents the operation ${\rm d}/{{\rm d}y}$. Utilizing the relationship between the vertical displacement field $\tilde {\eta }$ and the vertical velocity field $\tilde {u}_y = \mathcal {D}\tilde \eta /\mathcal {D} t$, we can rewrite (3.4) as

(3.5)\begin{equation} \frac{\mathcal{D} }{\mathcal{D} t} \left(\tilde{q}_z-\tilde{u}_x \frac{\rho_b'}{\rho_b}-\tilde{\eta} \frac{(\rho_b U')'}{\rho_b}\right) = 0, \end{equation}

i.e. the quantity inside the bracket is materially conserved. In other words, the disturbance vorticity $\tilde {q}_z$ is related to the horizontal disturbance velocity $\tilde {u}_x$ and the vertical displacement $\tilde {\eta }$ as

(3.6)\begin{equation} \tilde{q}_z=\tilde{u}_x \frac{\rho_b'}{\rho_b}+\tilde{\eta} \frac{(\rho_b U')'}{\rho_b}+\textrm{const}. \end{equation}

The constant term represents a bulk vorticity in the background flow. Since we are primarily interested in the relative vorticity generation $\tilde {q}_z$ with respect to this bulk vorticity, we can set the constant term to zero without loss of generality. From this general formulation, let us consider our special case where the base state flow is a simple shear flow, i.e. $U = \varGamma y$, and the base state particle number density has a top-hat distribution. Without loss of generality, we assume that $\varGamma > 0$. Since the particle concentration has sharp variations at locations $y = h/2$ and $y = -h/2$, the effective density $\rho$ of the fluid also varies sharply at these locations. The base state density $\rho _b(y)$ takes a constant value $\rho _1 = \rho _f$ outside the particle band and $\rho _2 = (\rho _f+\langle \phi _p \rangle \rho _p) > \rho _1$ within the particle band, as shown in schematic figure 4. These density jumps cause the locations of the jumps ($y = \pm h/2$) to act like interfaces separating different density fluids, marked as $\textrm {I}$ and $\textrm {II}$ in the figure 4. To begin with, we consider each of these interfaces in isolation and demonstrate that they support propagating waves due to disturbances.

Figure 4. Schematic illustrating the background simple shear flow, density jumps at the two interface locations labelled $\textrm {I}$ and $\textrm {II}$, and the corresponding interface disturbance fields. The initial interface displacement field ($\tilde {\eta }$) is depicted as a continuous sinusoidal curve, while its later stage is shown as a dashed curve, indicating its intrinsic propagation direction. The perturbation vorticity field ($\tilde {q}_z$) and perturbation vertical velocity fields ($\tilde {u}_y$) are also sinusoidal, with crests (troughs) represented by anticlockwise (clockwise) and upward (downward) arrows, respectively.

Consider interface $\textrm {I}$ at $y = h/2$, where the effective density drops from $\rho _2$ to $\rho _1$ (as we move along the positive $y$ direction). As a result, $\rho _b'(y) = -\Delta \rho \delta (y-h/2) < 0$, where $\Delta \rho = (\rho _2-\rho _1)>0$ and $\delta ({\cdot })$ represents a Dirac delta function. Let us assume that the interface is perturbed sinusoidally ($\tilde {\eta }$), as shown in the figure 4. From (3.6), we can deduce that a disturbance vorticity field is generated, given by $\tilde {q}_z=( \tilde {u}_x+\varGamma \tilde {\eta }) \rho _b'/\rho _b$. Generally, the associated horizontal perturbation velocity $\tilde {u}_x$ will have a discontinuity at the interface, which changes sign once we cross the interface. Physically, for a wave to be supported at the interface, there can be no self-induced $\tilde {u}_x$ for a wave-like solution at the interface. Thus, $\tilde {u}_x = 0$ at the interface. Then the generated vorticity disturbance is directly proportional to the interface perturbation as $\tilde {q}_z=\varGamma \tilde {\eta } \rho _b'/\rho _b$. Since $\varGamma > 0$, $\rho _b > 0$ and, as we saw earlier, $\rho _b' < 0$ at interface $\textrm {I}$, the generated vorticity disturbance will be out of phase with the interface displacement field. The maximum $\tilde {q}_z$ (anticlockwise) occurs at the troughs of the $\tilde {\eta }$ field, and the minimum $\tilde {q}_z$ (clockwise) occurs at the crests of the interface perturbation, as can be seen in figure 4 (the crests and troughs of the generated vorticity disturbances are shown as circular arrows). Since the density gradient is localized at the interface, the resulting vorticity disturbance would also be localized at the interface as a Dirac delta function with sinusoidal variation in the flow direction. The generated disturbance vorticity field induces a vertical flow velocity field $\tilde {u}_y$, which has a maximum at the positive sloping node and a minimum at the negative sloping node of the $\tilde {\eta }$. The vertical velocity field lags behind the interface displacement by $90^\circ$. The crests and troughs of the $\tilde {u}_y$ field are represented as upward and downward vertical arrows in figure 4. The $90^\circ$ phase difference serves as the perfect criterion for the propagation of the interface displacement as a wave. Upon visual inspection of figure 4, one can intuitively deduce that the upward $\tilde {u}_y$ at the positively sloping $\tilde {\eta }$ node and, similarly, the downward $\tilde {u}_y$ at the negatively sloping $\tilde {\eta }$ node would result in an intrinsic propagation of the wave leftward relative to the base state flow at the interface location. Also, the $90^\circ$ phase difference ensures that the wave would not experience any amplification or damping but only undergo propagation (see Carpenter et al. 2011).

This is similar to the generation of a propagating edge wave in a background shear flow where there is a jump in vorticity/shear rate present (see Vallis 2006). A generalized edge wave in a stratified fluid, which has both jumps in shear rate (from $\varGamma _2$ to $\varGamma _1$) and density (from $\rho _2$ to $\rho _1$) across an interface, should have a phase speed $c$ of the form

(3.7)\begin{equation} c = U_{interface}+\frac{(\varGamma_1\rho_1-\varGamma_2\rho_2)}{k (\rho_1+\rho_2)}. \end{equation}

Here, we do not have a jump in shear rate (i.e. $\varGamma _1 = \varGamma _2 = \varGamma$) but only a jump in density. Thus, the resulting wave at interface $\textrm {I}$ would propagate with a phase speed of $c_\textrm {I} = \varGamma h/2 - \varGamma \,At/k$, where $k$ is the spatial wavenumber in the $x$ direction of the disturbance and we used the definition of the Atwood number $At = (\rho _2-\rho _1)/(\rho _2+\rho _1)$, a non-dimensional number that frequently appears in the instability of density stratified flows. In non-dimensional terms (as one chooses the length scale to be $h$ and the time scale to be $\varGamma ^{-1}$), the phase speed is $c_\textrm {I}^* = c_\textrm {I}/(\varGamma h) = 1/2 - At/k^*$, or the dispersion relation $c_\textrm {I}^* k^* = k^*/2 - At$, which we will formally obtain as a large $k^* = k h$ (i.e. large separation $h$) asymptotic expression of the dispersion relation of the full system in § 4.2. Here, $()^*$ represents non-dimensional quantities.

Similarly, another propagating wave would be generated at interface II in isolation. At this interface, since the particle concentration varies such that $\rho _b' = \Delta \rho \delta (y+h/2) > 0$, the vorticity disturbance generated would be localized at the interface and in phase with $\tilde {\eta }$. As a result, the vertical velocity disturbance field thus produced would lead $\tilde {\eta }$ by $90^\circ$, and thus, the intrinsic propagation of the wave would be rightward relative to the base state flow at the interface location, as shown in figure 4. The propagation speed would be $c_\textrm {II} = -\varGamma h/2 + \varGamma \, At/k$ or $c_\textrm {II}^* = -1/2 + At/k^*$.

Now that we have established that there would be a leftward propagating wave at interface $\textrm {I}$ and a rightward propagating wave at interface $\textrm {II}$ when they are in isolation or, equivalently, when the interfaces are well separated (i.e. $h \rightarrow \infty$ or $k^* \gg 1$), let us consider the scenario as the separation $h$ between the interfaces is reduced. One can expect the interfacial waves to perceive other's presence and interact as they come closer. This is because, although the interfacial vorticity fields are localized Dirac delta functions, the vertical velocity fields typically exhibit exponential decay (wave evanescence) away from the interface location (e.g. $\exp ({-k\lvert y-h/2\rvert })$ as we see in § 4.2 as the eigenfunction associated with $\tilde {u}_y$). As the waves approach each other, they could interact. Still, for modal instability to occur, two essential conditions must be satisfied (see Carpenter et al. 2011): (i) the phase speeds of the waves should be stationary with respect to each other (‘phase locking’) and (ii) the relative phase of the waves should lead to the mutual growth of the interface disturbances. As the interfaces approach each other, the individual wave speeds also approach one another and are expected to become equal (and equal to zero, i.e. $c_\textrm {I} = c_\textrm {II} = 0$) for $k h = k^* = 2\, At$. However, along with this natural convergence, interactions play a role such that the waves become stationary relative to each other at a slightly larger separation (or non-dimensional wavenumber $k^*_{cutoff} > 2\, At$). The leftward propagating wave at interface I can slow down the rightward propagating wave at interface II and vice versa (for $\varGamma >0$), thus achieving phase locking at a larger separation. Once the phase locking is achieved, it can be maintained even though the isolated phase speeds are generally unequal (except at $k^* = 2\, At$) due to mutual interaction. Adjustments in the phase difference between the waves maintain an induced phase speed that exactly cancels the intrinsic propagation speed. Therefore, condition (i) would be satisfied for $0 < k^* < k^*_{cutoff}$ through adjustments in the relative phase difference of the waves.

Similar to the propagation criterion, upon visual inspection of figure 4, one can deduce that an upward $\tilde {u}_y$ component at the crests of $\tilde {\eta }$ and equivalently a downward $\tilde {u}_y$ component at the troughs of $\tilde {\eta }$ will lead to the growth of the wave. As the isolated waves become phase locked, the interaction occurs in such a way that the $\tilde {u}_y$ field of one wave at an interface and the $\tilde {\eta }$ field of the other interface satisfy this criterion, and vice versa. Thus, by condition (ii), the phase-locked waves mutually trigger amplification and arrest propagation, leading to instability through wave interaction for any smaller separation of the interfaces (or non-dimensional wavenumbers in the range $0 < k^* < k^*_{cutoff}$). This intricate interaction between the phase-locked waves is fundamental to understanding the mechanism behind the generation of modal instability in such dust-stratified fluid systems.

We now address the earlier caveat, highlighting an important distinction from the classical Taylor–Caulfield instability. In the Taylor–Caulfield instability, interfacial waves are generated due to a Boussinesq-type baroclinic torque driven by buoyancy/gravity effects. This occurs in a system with an overall stable stratification ($\rho _1 < \rho _2 < \rho _3$), where $\rho _1$ is at the top, $\rho _2$ is at the middle and $\rho _3$ is at the bottom layers. A pair of stable surface gravity waves are generated at each interface, separating these layers due to the Boussinesq baroclinic effects. One of them propagates leftward while the other propagates rightward; together, they interact to produce a stationary wave that is dampening at each interface. However, when the interfaces are brought closer, in a background shear flow ($\varGamma > 0$), the interaction between the leftward propagating wave at the upper interface and the rightward propagating wave at the lower interface leads to instability.

However, in our system, no gravitational/buoyancy effects are present. Therefore, no restoring mechanism could generate propagating waves from Boussinesq baroclinic effects. Instead, the oft-neglected non-Boussinesq baroclinic effects are responsible for wave generation, acting as a different type of restoring mechanism. The waves generated closely resemble edge waves or vorticity waves rather than surface gravity waves, as only one stable propagating wave is generated at each interface. Similar to the Taylor–Caulfield instability, instability in our system requires a leftward propagating wave at the top interface and a rightward propagating wave at the bottom interface (noting that this preference is due to $\varGamma > 0$ and would be reversed if $\varGamma < 0$). Thus, for instability to occur, $\rho _3$ must be smaller than $\rho _2$, which we have assumed to be the same as $\rho _1$. However, if the system were configured with $\rho _3 = \rho _1 > \rho _2$, the direction of waves at each interface would be reversed. In such a scenario, the interaction would only amplify their propagation speed, suppressing phase locking and avoiding any chance of instability. Similarly, if $\rho _3>\rho _2>\rho _1$ ($\rho _3<\rho _2<\rho _1$) then there would be leftward (rightward) propagation of waves at both the interfaces, whose interaction also can not produce instability. With the evidence of instability from EL simulations and an explanation of the mechanism involving interacting edge waves, we now proceed towards a quantitative evaluation of the growth rate of the instability using a LSA.

4. Linear stability analysis

In this section we employ an analytical approach, complemented by numerical assistance, to investigate the system more formally, illustrating the existence and criteria and quantifying the growth rate of the instability. To achieve this, we incorporate a continuum description of the particle phase, outlined below.

4.1. Two-fluid model

We adopt the Eulerian–Eulerian description of a particle-laden flow, as outlined by previous works such as Saffman (1962); Marble (1970); Druzhinin (1995); Jackson (2000); Kasbaoui et al. (2015). The dispersed phase, or particle phase, is characterized by a set of conservation equations inspired from the kinetic theory of gases, employing a mono-kinetic particle velocity distribution function. According to the method, the particle phase is considered a continuum fluid of zero pressure, valid for very dilute suspensions. The mass and momentum conservation equations for the fluid and particle phases in the semi-dilute regime, expressed in non-dimensional form, are

(4.1a)\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u} =0, \end{gather}

(4.1b)\begin{gather}\frac{\partial n}{\partial t}+\boldsymbol{\nabla}\boldsymbol{\cdot}(n\boldsymbol{v}) = 0, \end{gather}

(4.1c)\begin{gather}\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}\boldsymbol{u} ={-}\boldsymbol{\nabla}p+\frac{1}{Re} \nabla^2\boldsymbol{u}+M \frac{ n (\boldsymbol{v}-\boldsymbol{u})}{St}, \end{gather}

(4.1d)\begin{gather}\frac{\partial (n\boldsymbol{v})}{\partial t}+\boldsymbol{\nabla} \boldsymbol{\cdot} \left(n \boldsymbol{v}\boldsymbol{v}\right) = \frac{n (\boldsymbol{u}-\boldsymbol{v})}{St}, \end{gather}

where, as mentioned earlier, $\boldsymbol {u}$ represents the fluid velocity, $\boldsymbol {v}$ denotes the particle velocity and $n = \phi _p/\langle \phi _p \rangle$ is the normalized particle number density; but all depicted as fields here. Here onwards, we drop $()^*$ from non-dimensional quantities as we only deal with them unless specified otherwise. For non-dimensionalization, the length and time scales are set to the initial width of the particle band ($h$) and the inverse shear rate ($\varGamma ^{-1}$), respectively. The dimensional number density $\phi _p/V_p$ is normalized by $\langle \phi _p \rangle /V_p$ to obtain a non-dimensional measure for the particle concentration field denoted as $n = \phi _p /\langle \phi _p \rangle$, where $V_p$ represents the particle volume. The non-dimensional numbers include the Reynolds number ($Re=\varGamma h^2/\nu$), which quantifies fluid inertia, the Stokes number ($St = \varGamma \tau _p$), characterizing particle inertia, and, as mentioned earlier, the particle mass loading $M = \rho _p \langle \phi _p \rangle / \rho _f$. We have not accounted for particle interactions and inertial lift forces in our current formulation, although these effects could alter particle trajectories significantly. Both hydrodynamic and non-hydrodynamic interactions among dust particles can influence particle trajectories, affecting phenomena like coagulation and deposition (see Patra, Koch & Roy (2022) and references therein). In this study we focus on the highly dilute limit and neglect the role of any interactions. The non-zero slip velocity a particle has with its background local shear flow causes it to experience an inertial lift force, as derived by Saffman (1965) for a simple shear flow scenario. The magnitude of the Saffman lift force depends on the particle Reynolds number based on the local shear rate. In our problem this Reynolds number is small; hence, we disregard the effect of inertial lift.

4.1.1. Linearization and normal mode analysis of the inviscid equations

We disregard viscous effects in the analytical approach and focus solely on the inviscid scenario, where $Re \rightarrow \infty$, as we have seen that the mechanism of the instability is inherently inviscid. For stability analysis, we linearize the governing equations (4.1). The flow quantities are split into their base state, denoted by capital letters, and perturbation, denoted with a tilde, such as $\boldsymbol {u} = \boldsymbol {U}+\tilde {\boldsymbol {u}}$, $\boldsymbol {v} = \boldsymbol {V}+\tilde {\boldsymbol {v}}$, $p = P+\tilde {p}$ and $n = N+\tilde {n}$. We consider a two-dimensional stability analysis in the $x$–$y$ plane. A general base state of the form $\boldsymbol {U} =\boldsymbol {V}= U(y) \hat {\boldsymbol {x}}$ and $N = N(y)$ satisfies the governing equations (4.1). That is, it is assumed that there is no slip between the base state particle and fluid velocities. Perturbing the base state with two-dimensional infinitesimal disturbances of the form $\tilde {\boldsymbol {u}}(x,y,t)$, $\tilde {\boldsymbol {v}}(x,y,t)$, $\tilde {p}(x,y,t)$ and $\tilde {n}(x,y,t)$, we obtain the linearized version of the equations as

(4.2a)\begin{gather} \boldsymbol{\nabla} \boldsymbol{\cdot} \tilde{\boldsymbol{u}} = 0, \end{gather}

(4.2b)\begin{gather}\frac{\partial \tilde{n}}{\partial t} + U \frac{\partial \tilde{n}}{\partial x} + \tilde{v}_y \frac{{\rm d}N}{{\rm d}y} +N \boldsymbol{\nabla} \boldsymbol{\cdot} \tilde{\boldsymbol{v}} = 0, \end{gather}

(4.2c)\begin{gather}\frac{\partial \tilde{\boldsymbol{u}}}{\partial t} + U \frac{\partial \tilde{\boldsymbol{u}}}{\partial x} + \tilde{u}_y \frac{{\rm d} U}{{\rm d}y} \hat{\boldsymbol{x}} ={-}\boldsymbol{\nabla} \tilde{p}+M \frac{ N (\tilde{\boldsymbol{v}}-\tilde{\boldsymbol{u}})}{St}, \end{gather}

(4.2d)\begin{gather}\frac{\partial (N \tilde{\boldsymbol{v}})}{\partial t} + U \frac{\partial (N\tilde{\boldsymbol{v}})}{\partial x} + N \tilde{v}_y \frac{{\rm d}U}{{\rm d}y} \hat{\boldsymbol{x}} = \frac{ N(\tilde{\boldsymbol{u}}-\tilde{\boldsymbol{v}})}{St}. \end{gather}

Here $\tilde {\boldsymbol {u}} = \tilde {u}_x \hat {\boldsymbol {x}}+\tilde {u}_y \hat {\boldsymbol {y}}$ and $\tilde {\boldsymbol {v}} = \tilde {v}_x \hat {\boldsymbol {x}}+\tilde {v}_y \hat {\boldsymbol {y}}$, where $\hat {\boldsymbol {x}}$ and $\hat {\boldsymbol {y}}$ are the unit vectors in the $x$ and $y$ direction, respectively. While it may appear that $N$ could be scaled out of all the terms in (4.2d), it is retained because one must consider that in regions where there are no particles, $N = 0$, $\tilde {\boldsymbol {v}} = (N\tilde {\boldsymbol {v}})/ N$ cannot be defined in these empty regions. We use two-dimensional disturbances, following Squire's theorem (Squire 1933), according to which the most unstable modes should be two dimensional, which is valid for dusty flows as well (Sozza et al. 2022). To solve the system, we utilize a standard approach of normal mode analysis. Since the linearized equations (4.2) are homogeneous in $x$ and $t$, we assume a normal mode form for the solutions as $\{\tilde {\boldsymbol {u}},\tilde {\boldsymbol {v}},\tilde {p},\tilde {n}\} = \{\hat {\boldsymbol {u}},\hat {\boldsymbol {v}}, \hat {p}, \hat {n}\}(y)\exp ({{\rm i}(k x-\omega t)})$, to obtain the eigenvalue system, similar to the one in Saffman (1962) (see Appendix A). Here $k$ is the non-dimensional wavenumber in the $x$ direction (scaled by $h$) and $\omega$ is the non-dimensional angular frequency (scaled by $\varGamma$). The complex wave speed is defined as $c = c_R+{\rm i} c_I = \omega /k$. For temporal stability analysis (real valued $k$), the real part ${\rm Re}(c)=c_R$ determines the phase speed of the wave propagation and the imaginary part ${\rm Im}(\omega ) = c_I k = \sigma$ determines the growth rate. If ${\rm Im}(\omega )<0$, the mode is stable, while if ${\rm Im}(\omega )>0$, it is unstable. We need to solve the linear eigenvalue system equations (A2), seeking the eigenvalues $c$ (or $\omega$) and eigenfunctions $\{\hat {u}_x, \hat {u}_y, \hat {p},\hat {v}_x, \hat {v}_y, \hat {n}\}$, where $\hat {\boldsymbol {u}}= \hat {u}_x \hat {\boldsymbol {x}}+ \hat {u}_y \hat {\boldsymbol {y}}$ and $\hat {\boldsymbol {v}}= \hat {v}_x \hat {\boldsymbol {x}}+ \hat {v}_y \hat {\boldsymbol {y}}$.

Note that the particle velocity disturbance field influences the evolution of perturbation number density, although there is no feedback from number density perturbations to other quantities. To simplify the analysis, (4.2a,c,d) can be combined to obtain a single equation by eliminating variables $\tilde {u}_x$, $\tilde {p}$, $\tilde {v}_x$ and $\tilde {v}_y$. Following the approach outlined by Saffman (1962), Asmolov & Manuilovich (1998), this can be achieved in the modal space to obtain a simplified nonlinear eigenvalue system involving only two variables $\hat {u}_y$ and $\hat {n}$ as

(4.3a)\begin{gather} \big[\mathcal{U} (D^2-k^2)-\mathcal{U}''\big]\hat{u}_y+M D\big[(U-c) \varLambda N' \hat{u}_y\big] = 0, \end{gather}

(4.3b)\begin{gather}{\rm i}k (U-c)\varLambda \hat{n}+D[N \varLambda^2] \hat{u}_y=0, \end{gather}

where $\mathcal {U}= (U-c)(1+ M N \varLambda )$ denotes a modified base state velocity, and the damping factor $\varLambda = (1+{\rm i}k \, St (U-c))^{-1}$ describes the averaged frequency response of the particle phase to fluctuations in fluid velocity. We use $D({\cdot })$ or $({\cdot })'$ to represent the differential operator ${{\rm d}}{{\rm d}y}$, where generally the former one is reserved for perturbation quantities and the latter one reserved for base state quantities. Equation (4.3a) represents a modified form of the Rayleigh equation in the context of instability of dusty rectilinear flows, which we will now refer to as the ‘dusty Rayleigh equation’ or DRE for short. Note that the compact form of (4.3a) may misdirect the reader that the curvature of the number density field (i.e. $N''$) plays a role in the instability. However, the terms containing $N''$ exactly cancel out and do not have any role, which will be apparent from the form given in (A4a). A derivation of (4.3) can be found in Appendix A. These equations differ from those in Saffman (1962) in that the latter considers a uniform base state number density field, leading to the absence of terms containing gradients of particle concentration. Additionally, they consider a viscous case with finite Reynolds number effects. However, we consider an inviscid scenario and non-uniform particle distribution, resulting in DRE (4.3a) instead of the modified Orr–Sommerfeld equation obtained by Saffman (1962).

4.2. Linear stability analysis for inertialess ($St = 0$) particles and the dusty Rayleigh criterion

In this section we show that the instability is present even in the vanishing particle inertia limit, so the origin of the instability is attributed to the mass loading, which quantifies the two-way coupling. In the inertialess limit, i.e. $St = 0$, the damping factor is $\varLambda = 1$ and the modified velocity becomes a linear mapping of the actual base flow as $\mathcal {U} = (U-c)(1+ M N)$. Thus, (4.3) can be reduced to

(4.4a)\begin{gather} \rho\big[(U-c) (D^2-k^2)-U''\big]\hat{u}_y+\rho' \big[(U-c) D-U'\big]\hat{u}_y = 0, \end{gather}

(4.4b)\begin{gather}{\rm i}k (U-c) \hat{n}+ N' \hat{u}_y = 0, \end{gather}

where we denote $\rho := 1+M N$. The term $\rho$ is the equivalent of a variable density, where its variation contributes to the inertial term, leading to the generation of non-Boussinesq baroclinic vorticity. Moreover, the same (4.4) can also be derived from linearization and normal mode analysis of the single-fluid model (see Ferry & Balachandar 2001; Rani & Balachandar 2003), as in the limit of $St \rightarrow 0$, the two-fluid model reduces to a stratified incompressible fluid system as we have seen in § 3.

The dusty Rayleigh criterion: the classic Rayleigh equation results in a necessary criterion for instability known as the inflection point theorem, which states that the base state velocity profile should exhibit an inflection point within the domain, meaning that the quantity $U''$ should change sign somewhere within the flow domain. The equivalent criterion in the context of (4.4a) is that the quantity $\varSigma = D[\rho U']$ should change sign within the flow domain. We have already seen the same term $\varSigma$ in (3.6), which generates vorticity disturbances and, thus, instability. A derivation of the modified Rayleigh criterion/dusty Rayleigh criterion can be found in Appendix B. An equivalent statement for piecewise linear base state profiles is that the two interfaces must exhibit opposite-signed jumps in $(\rho U')$ across them.

We investigate the stability of a particle-laden simple shear flow, corresponding to the EL simulation in § 2.2, where an unbounded simple shear flow interacts with particles localized within a band, as illustrated in figure 1. The respective non-dimensional form of the linear base state velocity profile is $U = y$ and the piecewise constant top-hat number density profile is

(4.5)\begin{equation} N(y) = \begin{cases} 1, & \textrm{if } -\frac{1}{2} \leqslant y \leqslant \frac{1}{2}, \\ 0, & \textrm{otherwise}, \end{cases} \end{equation}

where, as mentioned earlier, the inverse shear rate ($\varGamma ^{-1}$) is used as the time scale and the width of the band ($h$) is used as the length scale. In our case of a simple shear flow, the DRE stated above simplifies to a sign change for $N'$ in the flow domain, i.e. the gradient of the base state number density profile must exhibit a sign reversal for instability. In another sense, for the piecewise profile in (4.5), the instability criterion requires opposite-signed jumps in $\rho U'$ (or $N$ here) at the interfaces $y = \pm 1/2$, which is satisfied here. While the number density profile $N(y)$ defined in (4.5) is discontinuous, its form supports sharp gradients at the locations $y = \pm 1/2$, across which the sign flip occurs. It may be easier to visualize this sign flip if we smooth the number density profile, as we will see in (4.9) and figure 7. Overall, the base state meets the essential conditions for instability. However, instability is only assured once explicitly proven, as the dusty Rayleigh criterion serves as a necessary condition rather than a sufficient one. This section aims to analytically establish the presence of instability and pinpoint the parameter ranges where it manifests.

For the linear velocity profile and top-hat number density profile, the stability equations (4.4a) reduce to $(D^2-k^2)\hat {u}_y = 0$ for all $y$ values except at the two locations where the number density profile has a discontinuity, i.e. at the interfaces $y = \pm 1/2$. The solution to this equation can be obtained analytically and is expressed piecewise for each layer as

(4.6)\begin{equation} \hat{u}_y = \begin{cases} A_1 {\rm e}^{{-}k y}, & y > 1/2, \\ A_3 {\rm e}^{k y}+A_4 {\rm e}^{{-}k y}, & \lvert y \rvert < 1/2, \\ A_2 {\rm e}^{k y}, & y <{-}1/2, \end{cases} \end{equation}

where the unknown constants $A_1$ to $A_4$ need to be obtained from appropriate boundary conditions. Note that the decaying boundary condition for $\hat {u}_y$ at far field is already accounted for in the solution, i.e. $\hat {u}_y(y \rightarrow \pm \infty ) = 0$, assuming $k>0$. The kinematic criterion requires the continuity of $\hat {u}_y$ across the interfaces, ensuring the continuity of interface displacements ($\hat {\eta }$), as they are related through ${\rm i}k (U-c) \hat {\eta } = \hat {u}_y$. Additionally, integrating (4.4a) across the discontinuous interfaces provides corresponding dynamic conditions. For a detailed derivation, see Appendix C. Together, these conditions yield a system of four equations involving the unknowns $A_1$ to $A_4$ and $c$, as

(4.7)\begin{equation} \begin{bmatrix} 1 & 0 & - {\rm e}^{k} & - 1 \\ 0 & 1 & -1 & -{\rm e}^{k} \\ \alpha_1 & 0 & \alpha_2{\rm e}^{k} & -\alpha_2 \\ 0 & \alpha_3 & -\alpha_4 & \alpha_4{\rm e}^{k} \end{bmatrix}\begin{bmatrix} A_1 \\ A_2 \\ A_3 \\ A_4 \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \end{equation}

where $\alpha _1 = k(1/2-c)-M$, $\alpha _2 = k(1/2-c)(1+M)$, $\alpha _3=k(1/2+c)-M$ and $\alpha _4 = k(1/2+c)(1+M)$. For a non-trivial solution to the system of (4.7), the determinant of the coefficient matrix must be zero, leading to the dispersion relation

(4.8)\begin{equation} c ={\pm} \frac{1}{2k}\sqrt{\frac{(k-2\,At)^2-At^2(2+k)^2{\rm e}^{{-}2k}}{1-At^2{\rm e}^{{-}2k}}}, \end{equation}

where the Atwood number ($At=(\rho _{max}-\rho _{min})/(\rho _{max}+\rho _{min})$) is related to the mass loading as $At = M/(M+2)$. Note that the eigenvalues $c$ appear in pairs, especially when ${\rm Im}(c) \neq 0$, they manifest as complex conjugates. Therefore, for instability to occur, ${\rm Im}(c)$ should not be zero. Equation (4.8) indicates the presence of a cutoff wavenumber ($k_{cutoff}$), below which only the instability can occur, i.e. long-wave instabilities. This critical wavenumber can be determined as the solution of the transcendental equation $M (2-k + (2+k){\rm e}^{- k})-2 k=0$. The variation of $k_{cutoff}$ with $At$ is shown in the figure 5(a). For instance, for a mass loading of $M=1 \ (\textrm {or}\ At=1/3)$, the critical wavenumber can be obtained as $k_{cutoff} \approx 1.028$. The resulting unstable modes are stationary since the corresponding ${\rm Re}(c) = 0$. Conversely, the modes are neutrally stable propagating waves for shorter wavelengths, i.e. when $k > k_{cutoff}$. In the limit of small $k$ values, instability is always present but with a lower growth rate, as evidenced by the scaling $\omega \sim \pm {\rm i} \,\sqrt {k}\, \sqrt {At/(1+At)}$.

Figure 5. (a) The variation of the cutoff wavenumber $k_{cutoff}$, at which the instability disappears, and the optimum wavenumber $k_{max}$, at which the maximum growth occurs, are plotted against the Atwood number for a top-hat number density profile. (b) The variation of the maximum growth rate $\sigma _{max}$, corresponding to $k_{max}$, with $At$ is shown for the same number density profile.

Upon substituting the solution for $c$ in (4.8) back into (4.7), the amplitudes $A_1$ to $A_4$ can be determined, as detailed in Appendix C. The dispersion relation (4.8) is plotted in figure 6, using continuous lines, for two different mass loading values. It can be observed from figure 6(a) that, for $k < k_{cutoff}$, the growth rate of the modes increases until reaching a maximum and then decreases for any given mass loading. Consequently, an optimal wavenumber ($k_{max}$) exists at which the maximum growth ($\sigma _{max}$) occurs. This optimal wavenumber can be obtained by solving the transcendental equation ${\rm e}^{2 k} (k-2\,At)+2\,At^2 (1+2\, At)\,(1-At+ k)+{\rm e}^{-2 k}\,At^4 (2+k) = 0$, derived from (4.8) using the optimization criteria ${\rm d} (c k)/{\rm d} k = 0$. Figure 5(a) displays the variation of $k_{max}$ with $At$ while figure 5(b) shows the variation of $\sigma _{max}$ with $At$. For instance, for $M=1 (\textrm {or}\ At=1/3)$, the non-dimensional wavenumber corresponding to the maximum growth rate is $k_{max} \approx 0.504$ and the maximum growth rate is $\sigma _{max} = k_{max}\, {\rm Im}(c(k_{max})) \approx 0.244$.

Figure 6. Dispersion relation for the $St = 0$ case, for two different mass loadings ($M=1$ – orange and $M=2$ – blue), obtained analytically (for a top-hat number density profile) and numerically (for two different smooth number density profiles: $m=1$ and $m=4$): (a) growth rate $\sigma$ (imaginary part of $\omega$) vs $k$, (b) real part of $\omega$ vs $k$.

From figure 6(b), it is evident that for $k > k_{cutoff}$, the waves propagate in opposite directions and attain a speed of $\omega \sim \pm (k/2 - At)$ as $k \rightarrow \infty$ (shown as asymptotes in the figure for $M=1$ in grey). This implies that the waves propagate without any interaction, as they are well separated by the distinct interfaces on which they exist. As we discussed the instability mechanism in § 3, we obtained the same dispersion relation earlier for isolated waves at the interface. The natural phase speed matching of the isolated left and right propagating waves occurs at $k = 2\, At$, as indicated by the crossing of these asymptotic lines in the dispersion curve. However, in practice, this matching occurs at $k_{cutoff} > 2\, At$ due to their interaction, as seen from the figure.

For the linear velocity profile and the top-hat number density profile, (4.4b) simplifies to $(y-c) \hat {n}=0$ everywhere except at the interfaces $y=\pm 1/2$. For the discrete modes (which corresponds to $y \neq c$), this equation yields $\hat {n} = 0$ everywhere except at the interfaces. Considering the interface discontinuity and conservation of the total number of particles, one finds that $\int _{-\infty }^{\infty } \hat {n}\, {{\rm d}y} = 0$, which implies that $\hat {n} \propto \delta (y-1/2)-\delta (y+1/2)$.

To verify the analytical results, we numerically solved the linear eigenvalue differential equation (4.4a) using a standard Chebyshev spectral collocation method. To avoid issues arising from the discontinuity of the base state number density profile, we employed a smooth generalized Gaussian profile for the number density:

(4.9)\begin{equation} N(y) = \exp \left\{-\left(\frac{y}{y^*}\right)^{2 m} \right\}, \quad \textrm{with} \ m \in \mathbb{N}. \end{equation}

Here $y^* = ( 2 \varGamma (1+1/(2 m) ) )^{-1}$, ensuring that the normalization yields $\int _{-\infty }^{\infty }N(y)\, {{\rm d}y} = 1$; $\varGamma ({\cdot })$ denotes the gamma function and $m$ is the smoothness parameter. The number density profile exhibits maximum smoothness for small integer values of $m$, whereas for larger values of $m$, it develops sharp variations. As $m$ tends to infinity, the profile approaches the singular top-hat profile described in (4.5), as ensured by the normalization. The plots in figure 7 depict the variation of the smooth base state number density profile and the corresponding stability-determining quantity $\varSigma$ for various smoothness parameters $m$ within the flow domain. The Chebyshev collocation points ranging from $y \in [-1,1]$ are transformed to $y \in [-R,R]$, where $R$ is chosen to be sufficiently large to mimic infinity. To enhance the efficiency of the numerical method by capturing the sharp variations near the interfaces more effectively, we use the transformation as in Govindarajan (2004), which ensures that more collocation points are clustered near $y = 0$. Since the base state profiles are now smooth, there is no need to apply interface conditions. Instead, only the far-field decay of the eigenfunctions needs to be enforced.

Figure 7. (a) The smooth base state number density profile corresponds to the generalized Gaussian for various smoothness parameters $m$. (b) The corresponding parameter $\varSigma$ (scaled with mass loading $M$) in the background simple shear flow, which determines the stability, is plotted in the flow domain.

Figure 6 illustrates the corresponding dispersion relation obtained for two different smooth profiles corresponding to the smoothness parameter $m=1$ (Gaussian) and $m=4$, depicted using dotted and dashed lines, respectively. Figure 6(a) shows that the smooth variation in the number density profile also causes instability. The trend of the dispersion curves remains the same, with a maximum growth rate at some optimum wavenumber. However, the symmetry of the curve before and after this wavenumber is compromised for smooth profiles. Also, the cutoff wavenumber $k_{cutoff}$ at which the instability ceases to exist differs as the index $m$ changes. Note that, for the largest value of $m=4$, the numerical results compare well with the analytical results, with a better match expected for larger values of $m$.

Figure 6(b) displays the variation of ${\rm Re}(\omega )$ with $k$, indicating the emergence of counterpropagating edge waves once the system is in the stable regime. The curves displayed are only for the analytical dispersion relation obtained for a top-hat number density profile. For smooth number density profiles, stable discrete modes are absent. The spectrum is purely continuous. The smooth variation of $N'$ in this case, as opposed to the zero $N'$ for a top-hat profile everywhere except the jump location, results in a logarithmic branch point at the critical layer ($y=c$), as in the case of the continuous spectrum of inhomogeneous shear flows (Balmforth & Morrison 1995). The vorticity continuous spectrum eigenfunctions would be a combination of a delta-function singularity and a non-local Cauchy principal-value singularity (see Van Kampen 1955; Case 1959). However, the mechanistic picture of the interaction between edge waves offered earlier would persist despite the absence of discrete modes in the stable regime for smooth profiles. Interestingly, for smooth profiles with sufficiently ‘steep’ transition regions (${m\gg 1}$), a wave packet comprised of the continuous spectrum modes camouflages as a discrete mode known as a quasimode or a Landau pole (Schecter et al. 2000). The quasimodes at each transition region can then interact and lead to instability, as seen previously in the computed growth rates for the smooth number density profile cases.

4.3. Effect finite particle inertia ($St \neq 0$)

For any finite $St$, one must solve (4.3) for simple shear flow ($U = y$). However, it is an analytically cumbersome task even for the top-hat number density profile in (4.5). This complication is due to the modified velocity $\mathcal {U}$ and the damping factor $\varLambda$. A small $St$ perturbation analysis can be performed to obtain asymptotic solutions in terms of Whittaker functions. However, solving the equivalent linear eigenvalue system of (A2) numerically for a smooth number density profile would be more feasible. After eliminating $\hat {u}_x$ and $\hat {p}$ from (A2a,c,d), the system can be reduced to the form

(4.10)\begin{equation} \begin{bmatrix} l_1 & \dfrac{M k}{St} l_2 & -\dfrac{{\rm i}k^2 M N}{St} & 0\\[8pt] -\dfrac{{\rm i}}{k\, St} D & l_3 & U' & 0\\[8pt] -\dfrac{1}{St} & 0 & l_3 & 0\\ 0 & {\rm i} k N & l_2 & {\rm i}k U \end{bmatrix}\begin{bmatrix} \hat{u}_y\\ \hat{v}_x\\ \hat{v}_y\\ \hat{n} \end{bmatrix} = \omega \begin{bmatrix} (D^2-k^2) & 0 & 0 & 0 \\ 0 & {\rm i} & 0 & 0 \\ 0 & 0 & {\rm i} & 0 \\ 0 & 0 & 0 & {\rm i} \end{bmatrix} \begin{bmatrix} \hat{u}_y\\ \hat{v}_x\\ \hat{v}_y\\ \hat{n} \end{bmatrix}, \end{equation}

with the eigenvalues $\omega$ and the eigenfunctions $\{ \hat {u}_y,\hat {v}_x,\hat {v}_y,\hat {n} \}$. Here $l_1 = (k U-{{\rm i} M N}/{St}) D^2-({{\rm i} M N'}/{St}) D -k (U''+k^2 U-{{\rm i} k MN}/{St} )$, $l_2 = N'+ND$ and $l_3 = {\rm i} k U+{1}/{St}$. We solve the system of (4.10) numerically for a simple shear flow ($U = y$) with a smooth base state number density profile as given by (4.9), with decaying boundary conditions for all eigenfunctions in the far field.

The results obtained are presented in figure 8. Figure 8(a) depicts the growth rate versus the $k$ curve for various $St$ values, considering a smooth number density profile with $m=4$, for two different mass loading values. The corresponding curve for $St=0$ with a top-hat number density profile is also displayed for comparison. It is evident that as $St$ increases, the growth rate decreases for all mass loading values and wavenumbers. Furthermore, the cutoff wavenumber $k_{cutoff}$ decreases with increasing $St$. However, upon closer inspection, it is observed that with a finite Stokes number, the instability persists for $k > k_{cutoff}$, albeit with a significantly lower growth rate. In figure 8(b) the deviation of the growth rate corresponding to finite $St$ from the $St=0$ case is plotted as a function of Stokes number for various mass loading values. The wavenumbers are chosen to correspond to the fastest-growing modes for the corresponding mass loading values. The results are obtained numerically for a smooth number density profile of $m=4$. Analytically obtained asymptotes (using a small $St$ perturbation analysis) for the respective cases with top-hat number density profiles are plotted for comparison. The figure demonstrates that the growth rate decreases as the Stokes number increases.

Figure 8. (a) Growth rate $\sigma$ vs $k$ for two different mass loadings, $M=1$ (orange) and $M=2$ (blue), for various $St$ values obtained numerically for a smooth number density profile ($m=4$). The analytical result for the $St=0$ case with a top-hat number density profile is also shown for comparison. (b) The difference in growth rate for a finite $St$ case from the $St=0$ case, plotted versus $St$ for various combinations of $M$ and $k$. Here, $k$ is chosen to be approximately the optimum wavenumber to the respective $M$ value. Continuous lines represent the numerical results for a smooth profile ($m=4$), while dashed lines represent the analytic asymptotes for a top-hat profile.

Figure 9(a) presents a contour plot of the growth rate in the $k$ vs $St$ plane for a mass loading $M=2$, obtained numerically, for a smooth number density profile of $m=4$. The plot illustrates that the growth rate decreases with $St$ and increases with $M$. This implies that particle inertia stabilizes the instability, whereas the mass loading (representing the two-way coupling strength) has a destabilizing effect. This qualitative trend would also hold for other mass loading values, though they are not shown here. In figure 9(b) the variation of growth rate with mass loading is depicted for various combinations of $k$ and $St$. This plot reiterates the deduction about the dampening of instability by $St$ and the strengthening of instability by $M$. It is important to note that the instability persists even in the limit of $St = 0$, whereas it vanishes in the $M=0$ limit (i.e. in the one-way coupling case). The analysis presented in this section confirms the existence of an instability in the system under consideration. The source of instability is attributed to the two-way coupling between the particles and the fluid, and it is observed that the instability can be dampened by the particle inertia.

Figure 9. (a) A contour plot of growth rate $\sigma$ in the $k$ vs $St$ plane for a mass loading of $M = 2$. (b) The variation of growth rate versus mass loading for various combinations of $k$ and $St$ values: the dotted line represents $St = 10^{-3}$, the continuous line represents $St = 10^{-2}$ and the dashed line represents $St = 10^{-1}$. The results are obtained numerically for a smooth base state number density profile with $m=4$.

5. Comparison of EL results with LSA results

In the previous sections we demonstrated the existence and mechanism of the instability using a linearized continuum model for the system. What remains is a quantitative comparison of the predictions from LSA with fully nonlinear EL simulations.

We conducted a series of EL simulations across various parameter ranges to obtain the dispersion curve. The simulation set-up is similar to that in § 2.2. The dimensional quantities are set to: $\rho _f = 1.0\ \textrm {Kg}\ \textrm {m}^{-3}$, $\mu _f = 1.5 \times 10^{-5} \ \textrm {Kg}\ \textrm {m}^{-1}\ \textrm {s}^{-1}$, $\varGamma = 12.65\ \textrm {s}^{-1}$, $d_p = 4.62 \ \mathrm {\mu } \textrm {m}$ and $\rho _p = 1000 \ \textrm {Kg}\ \textrm {m}^{-3}$. As a result, in these simulations, the Stokes number ($St$) was kept constant at $10^{-3}$ and the density ratio was fixed to $\rho _p/\rho _f = 1000$. To ensure a fair comparison with the inviscid LSA, the EL simulations were conducted with a fixed $Re_{L_x} \approx 5000$, which is sufficiently high to make viscous effects negligible. The simulation domain size was set as $L_x = 16\,666 d_p$, $L_y = 3 L_x$ and $L_z=3 d_p$. The average volume fraction $\langle \phi _p \rangle$ of particles within the band was adjusted among $10^{-3}$ and $2\times 10^{-3}$ to achieve various mass loading values, $M = 1$ and $M=2$, respectively. To confine only one wave within the domain in the $x$ direction, we fixed the dimensional wavelength to be $\lambda = L_x$. By adjusting the bandwidth $h$, we obtained different non-dimensional wavenumber values, ranging from $k = 0.125$ to $1.6$, where the non-dimensional wavenumber $k = 2{\rm \pi} h/\lambda$. In all selected cases, the ratio $h/d_p$ was set to be large (of the order of $3 \times 10^2$ to $4 \times 10^3$), ensuring that fluctuations caused by discrete particle forcing remained well below the viscous dissipation scale. This configuration enabled fluid–particle coupling primarily through collective particle dynamics at scales comparable to $h$, rather than discrete effects at inter-particle distances. Since $L_x$ is fixed, varying $h$ leads to a change in the ratio $L_x/h$ across the range from $1.25 {\rm \pi}$ to $16 {\rm \pi}$. However, $L_y$ remains sufficiently large in all these cases to avoid any possible interactions with other periodic simulation boxes in the $y$ direction. Though the domain size in the spanwise ($z$) direction is limited ($L_z = 3 d_p$), the randomness in particle distribution can induce perturbations in the spanwise direction. However, as mentioned earlier in § 4.1.1, an equivalent of Squire's theorem for the Euler–Euler model for particle-laden flows suggests that the disturbance with the maximum growth rate would be two dimensional. We presume the same applies to EL simulations, with the fastest-growing modes in the flow ($x$) and gradient ($y$) directions. Therefore, we restrict our study to a limited spanwise domain size. Additionally, we maintain a large $h/d_p$ ratio in all the simulations, meaning that discrete effects are negligible. Only collective effects (or fluctuations on the scale of hundreds of particles) matter.

The initial conditions of the numerical simulations consist of a combination of the base state (a simple shear flow with a top-hat number density profile) and perturbations. Unlike in § 2.2, here, the initial perturbation is selected differently by using the eigenmodes obtained from LSA. To perturb our system, we utilize the analytic expressions for the eigenmodes of the velocity field obtained for the corresponding $St = 0$ case. The initial particle number density field is left unperturbed since the eigenmodes are theoretically singular Dirac delta functions. Although this initial arrangement may not correspond precisely to an eigenmode of the system under consideration (due to the omission of finite $St$ aspects and perturbations in the number density field), it will closely resemble the eigenmode. As time progresses, the applied perturbations are expected to excite the most unstable mode, i.e. the respective eigenmode of the system. The initial perturbation fields can be visualized in the leftmost panels of figure 10. To ensure that the simulations capture the linear regime described by LSA and to delay any nonlinear effects, the perturbations are initialized with a small relative amplitude $\epsilon = 10^{-2}$. The location of the particles are randomly initialized within each cell inside the particle band, defined by $\lvert y \rvert \leqslant h/2$.

Figure 10. Panel (a) show the time evolution of the perturbation vorticity field $\tilde {q}_z$ (scaled by $\epsilon \varGamma$), while (c) depicts the total particle number density field $\phi _p/\langle \phi _p\rangle$. The results are from a two-way coupled simulation with $M=1$ and $St=10^{-3}$, examining three sets of non-dimensional wavenumbers: (a–e) $k = 0.25$, (f–j) $k = 0.5$ and (k–o) $k = 1.2$. The $x$ coordinate is scaled with the wavelength $\lambda$ and the $y$ coordinate is scaled with the band width $h$ in the plots. The snapshots are zoomed in and cropped to focus on the particle band.

Figure 10 illustrates the time evolution of the perturbation vorticity field (scaled by its initial maximum value) in the top panels and the particle number density field in the bottom panels, for a case with $M=1$ and $St = 10^{-3}$. The results are shown for three different non-dimensional wavenumbers: $k=0.25$, $k=0.5$ and $k=1.2$. As before, the snapshots are zoomed in and cropped around the particle band for better visualization. The initial evolution of the perturbation fields confirms the excitation of the respective eigenmodes. For the case of smaller wavenumber $k=0.25$ (panels a–e), it can be seen that the perturbations grow over time and the vorticity field amplifies and spreads across a larger region, indicating the presence of instability. For $k=0.5$ (panels f–j), the instability becomes more pronounced and transitions to the nonlinear regime rapidly, as expected theoretically, since the maximum growth corresponds to a non-dimensional wavenumber closer to $k=0.5$. The theory predicts no linear instability for the larger wavenumber $k=1.2$ (panels k–o), which is also evident from the snapshots where there is minimal growth of the vorticity field. It can be observed that, in all the cases, although the number density field is initially not perturbed, eventually, the eigenmodes are getting excited. The early evolution of the number density is linear, as predicted; however, as time progresses, nonlinear effects become apparent. However, at all times and for all wavenumbers, the evolution of the number density field remains coherent with the corresponding perturbation vorticity field. This correspondence also holds theoretically for a top-hat profile, as we have already seen using LSA that the vorticity perturbation and number density perturbation fields are both Dirac delta functions. The number density snapshots show that the case with wavenumber $k=0.5$ transitions to the nonlinear regime much faster than the others.

In order to determine the total perturbation growth rates from the present simulations, we calculate the disturbance kinetic energy associated with the perturbations as

(5.1)\begin{equation} E = \int \tfrac{1}{2}(\boldsymbol{u}-\boldsymbol{U})\boldsymbol{\cdot}(\boldsymbol{u}-\boldsymbol{U})\, {\rm d}V, \end{equation}

where $\boldsymbol {U} = \varGamma y \hat {\boldsymbol {x}}$, the base state simple shear flow, is subtracted from $\boldsymbol {u}$, the total fluid velocity obtained from EL simulations, to obtain the disturbance fluid velocity. The integration is performed over the entire volumetric domain of the periodic simulation box.

Figure 11(a) shows the evolution of total perturbation energy ($E$), scaled with the initial value ($E(t=0) = E_0$), computed from EL simulations, presented in a semi-logarithmic scale for various non-dimensional wavenumbers $k$, corresponding to a mass loading of $M=1$. The plots exhibit a linear trend at initial times, indicating an exponential dependence on time. If the growth rate of velocity perturbations is denoted as $\sigma$, then the growth rate of energy perturbations would be $2 \sigma$. Based on this argument, one may derive an expression to assess the growth rate $\sigma$ from EL simulations as

(5.2)\begin{equation} \sigma = \frac{1}{2E}\frac{{\rm d} E}{{\rm d}t}. \end{equation}

Figure 11(b) shows the time evolution of the growth rate estimated for EL simulation results using the expression given in (5.2). Unlike the prediction from LSA, which suggests a constant value, the instability growth rate exhibits variation over time in EL simulations. The figure indicates that the growth rate peaks between $t = 0$ and $t=2$, depending on the seeded mode. The initial transient behaviour may be attributed to imperfections in the initial conditions. The time window surrounding the peak growth rate in figure 11(b) corresponds to the exponential growth of kinetic energy observed in figure 11(a), thereby closely aligning with the dynamics predicted by LSA. Eventually, the growth rate decreases as the perturbation kinetic energy saturates, with the possibility of a later increase due to nonlinear effects. An estimate for comparison with LSA would be the peak value of the growth rate for EL simulations obtained from (5.2). The non-dimensional growth rates $\sigma$ are thus obtained and plotted against the corresponding non-dimensional wavenumber $k$ for two different mass loading values in figure 12(a), represented by circle markers. The growth rate numerically obtained from LSA for a smooth number density profile ($m=4$) is also compared. The results show good agreement, although some discrepancies are observed in the numerical values. Considering that we are comparing completely different simulation classes: fully nonlinear EL simulations with LSA of the Euler–Euler model for the system under consideration, these differences are expected. Furthermore, the growth rate obtained from EL simulations indicates that energy perturbations decay beyond the critical wavenumber, contrary to what linear theory predicts. This could be attributed to the viscous effects in EL simulations.

Figure 11. The evolution of (a) total perturbation energy $E$ (normalized by its initial value) and (b) the estimate for the instantaneous growth rate with time, obtained from EL simulations, for mass loading $M=1$, for various $k$ values.

Figure 12. The growth rate $\sigma$ obtained from EL simulations for particles with $St = 10^{-3}$ is plotted (a) against $k$ for two mass loadings $M=1$ (orange colour) and $M=2$ (blue colour), and (b) against $M$ for $k = 0.5$. Various estimates for the growth rate are indicated by different markers: $\circ$ denotes the peak value of the growth rate ($\textrm {max}(\sigma )$) estimated from the total perturbation energy, $\square$ represents the average value of the growth rate ($\textrm {avg}(\sigma )$) in a time window $\Delta t = 0.5$ about the peak growth rate of the total perturbation energy, and $\diamond$ indicates the peak growth rate obtained from the energy of the seeded mode ($\textrm {max}(\sigma _s)$). For comparison, the corresponding curves numerically obtained from LSA for a smooth number density profile of $m=4$ are also shown using dotted lines.

In order to quantify the contribution of a specific wave mode $k$ to the overall dynamics, we compute the kinetic energy associated with this mode using Fourier decomposition as

(5.3)\begin{equation} E_k = \int_{{-}L_z/2}^{L_z/2}\int_{{-}L_y/2}^{L_y/2} \frac{1}{2}\, \overline{\hat{\boldsymbol{u}}_k(y,z,t)} \boldsymbol{\cdot}\hat{\boldsymbol{u}}_k(y,z,t) \, {{\rm d}y}\, {\rm d}z, \end{equation}

where $\overline {({\cdot })}$ denotes complex conjugation and $\hat {\boldsymbol {u}}_k$ is the Fourier amplitude of the perturbation velocity field, given by

(5.4)\begin{equation} \hat{\boldsymbol{u}}_k(y,z,t) = \frac{1}{\sqrt{2 {\rm \pi}}} \int_{{-}L_x/2}^{L_x/2} (\boldsymbol{u}-\boldsymbol{U}) \exp(-{\rm i}kx) \, {{\rm d}x}. \end{equation}

The normalization for the Fourier amplitude is chosen such that Plancherel's identity yields $\int E_k \, {\rm d}k = E$. The peak growth rate corresponding to the seeded eigenmode can thus be extracted using (5.3) with (5.2), and are also shown in figure 12 using diamond markers. These growth rates are also adequately consistent, qualitatively and quantitatively, with the LSA results. Additionally, the figure shows an average estimate of the growth rate over a non-dimensional time window $\Delta t = 0.5$ centred around the peak value of total perturbation energy, depicted using square markers, which also compares well with the LSA results. The differences between these various growth rate estimates can also be observed to be very small.

Figure 12(b) displays the growth rate estimates from EL simulations for the $k=0.5$ case plotted for various mass loading values. As the mass loading increases, the growth rate also increases, indicating that the strength of the two-way coupling determines the strength of the instability. The trend in growth rate aligns well with the LSA results (shown as a dotted curve). Below a critical mass loading, however, the EL simulations show damped modes instead of the neutral modes observed in LSA, likely due to the inherent viscous nature of EL simulations, as mentioned earlier.

6. Conclusion

In this study we have investigated a novel type of instability arising from the interaction between a simple shear flow and a non-uniform distribution of particles. Individually, each component is stable; a simple shear flow remains stable against infinitesimal perturbations and a localized band of particles is stable without any gravitational or buoyancy effects. However, when considering the system as a whole, the momentum feedback from the particles to the fluid phase renders the system unstable. We utilized EL simulations to show the existence of instability, treating the fluid phase as a continuum and the particles as discrete using Eulerian and Lagrangian descriptions, respectively. The two-way coupling between the fluid and particle phases is crucial for the observed instability. The strength of the momentum feedback from particles to the fluid is directly proportional to the particle mass fraction and inversely proportional to particle inertia. Consequently, increasing the particle mass fraction enhances the instability while increasing particle inertia suppresses it. The simulations were conducted at high Reynolds numbers, indicating that the instability originates from inviscid effects. Moreover, we conducted simulations where we disabled the momentum feedback from particles to the fluid, while retaining the momentum exchange from the fluid to the particle phase. As anticipated, the system remained stable under these conditions, with particles solely advected by the shear flow.

Furthermore, a continuum model of the particle phase is employed to illustrate this instability's modal nature and explain its generation mechanism. In the semi-dilute limit the particle phase can be modelled as a separate pressureless fluid. The model adopts an Eulerian approach for particle and fluid phases, known as the two-fluid model. Linear stability analysis of this model was conducted under the $St = 0$ and $St \ll 1$ limits to quantify the growth rate of instability, utilizing analytical and numerical techniques. The analytical investigation primarily focused on a simple top-hat distribution of particles, while a numerical treatment was reserved for smooth, localized particle distributions. In both scenarios, the analysis demonstrated that instability emerges as the momentum feedback from particles to the fluid phase is considered. Surprisingly, the instability persists even in the $St \rightarrow 0$ limit, suggesting that although it originates from particle inertia, its existence does not solely depend on inertia when the fluid–particle coupling is accounted for. However, increasing $St$ results in a damping effect on the growth rate of instability. The growth rate estimates from EL simulations matched the LSA results reasonably well.

To gain a mechanistic view of the instability, we examine the regime of small particle inertia ($St \rightarrow 0$). In this limit, the two-fluid model simplifies into a single-fluid model that describes the continuum evolution of a fluid with an effective density due to the suspended particles. The non-uniformity in particle distribution is thus reflected in the effective density of this fluid. The system now resembles a density stratified fluid capable of supporting propagating edge waves at interfaces where vorticity or density exhibits discontinuities. Our system has two density interfaces, which individually support propagating edge waves generated due to non-Boussinesq baroclinic effects in isolation in a background shear flow. Unlike in the case of classical edge waves, the baroclinic torque arises from the misalignment between base state density stratification and disturbances in fluid acceleration. The propagating waves at both interfaces feel each other's presence once brought closer, and they interact through phase locking and mutual amplification, culminating in the instability observed.

The proposed mechanism effectively explains the generation of the novel instability, showing that the effects arise from the local mass loading of particles in the finite layer and not from particle inertia, i.e. as they behave as Lagrangian tracers. The particle inertia has a modifying effect on instability, as evidenced by the LSA. The analysis assumes inviscid conditions, meaning viscous dissipation plays no role in the instability's generation. The energy fueling its growth is however extracted from the infinite reservoir of the background shear flow.

The present analysis has made several assumptions, and the relaxation of many of those would augment the instability found in the present study. The background flow is a simple shear flow, thus disallowing any shear instabilities that might arise (Drazin & Reid 2004). We have also neglected the effects of gravitational settling, non-zero fluid inertia, concentration-dependent viscosity and hydrodynamic interactions. As was discussed earlier, in a simple shear flow of uniformly distributed negatively buoyant inertial particles, velocity perturbations can lead to a preferential concentration of particles in regions of low vorticity. Kasbaoui et al. (2015) showed that the variation of gravitational force exerted on the suspension thus induced would result in an algebraic instability. Ignoring gravitational effects, if the effects of fluid inertia were included instead, the particles would experience lift forces. In 2.2 we provided justification for ignoring lift forces in the present study. However, with an increase in the shear Reynolds number, the lift force would be non-negligible. In such scenarios, the observation of Drew (1975) that there can be an instability in a bounded simple shear flow purely due to the lift force needs to be further explored in the context of the two-way coupling instability observed in the present study. A departure from the diluteness approximation would manifest first as a concentration-dependent viscosity and then as non-zero particle pressure. With the former physics, non-uniformity in particle concentration can lead to viscosity contrasts in the suspension, potentially causing short-wave viscous instabilities (see, e.g. Hooper & Boyd 1983; Hinch 1984; Sahu & Govindarajan 2011). The latter, particle pressure due to hydrodynamic interactions, is responsible for shear-induced migration in dense suspensions (Leighton & Acrivos 1987). Shear-induced migration would be absent in a simple shear flow. However, the perturbation-induced migration could lead to a short-wave instability depending on the importance of concentration-driven diffusion relative to shear-induced migration (Goddard 1996). Coupling even some of the physics mentioned above with the novel instability found in the present study would pave the way for a better understanding of instabilities in dusty shear flows and how they can have fundamentally different transition routes than their particle-free counterparts.