Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Balci, Adnan
Brøns, Morten
Herrada, Miguel A
and
Shtern, Vladimir N
2015.
Vortex breakdown in a truncated conical bioreactor.
Fluid Dynamics Research,
Vol. 47,
Issue. 6,
p.
065503.
Naumov, I. V.
Dvoynishnikov, S. V.
Kabardin, I. K.
and
Tsoy, M. A.
2015.
Vortex breakdown in closed containers with polygonal cross sections.
Physics of Fluids,
Vol. 27,
Issue. 12,
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2016.
Instability of a water-spout flow.
Physics of Fluids,
Vol. 28,
Issue. 3,
Herrada, Miguel
and
Shtern, Vladimir
2016.
Stability of thermal convection in a rotating cylindrical container.
Physics of Fluids,
Vol. 28,
Issue. 8,
Carrión, Luis
Herrada, Miguel A
Shtern, Vladimir N
and
María López-Herrera, José
2017.
Patterns and stability of a whirlpool flow.
Fluid Dynamics Research,
Vol. 49,
Issue. 2,
p.
025519.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2017.
Topology changes in a water-oil swirling flow.
Physics of Fluids,
Vol. 29,
Issue. 3,
Naumov, Igor V.
and
Podolskaya, Irina Yu.
2017.
Topology of vortex breakdown in closed polygonal containers.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
263.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2017.
Topology and stability of a water-soybean-oil swirling flow.
Physical Review Fluids,
Vol. 2,
Issue. 2,
Niyogi, Kaustav
Torregrosa, Maria M.
Marin, Guy B.
Heynderickx, Geraldine J.
and
Shtern, Vladimir N.
2018.
On the mechanisms of secondary flows in a gas vortex unit.
AIChE Journal,
Vol. 64,
Issue. 5,
p.
1859.
Podolskaya, I Yu
Bakakin, G V
and
Naumov, I V
2018.
Investigating the structure of a vortex flow in the closed polygonal containers.
Journal of Physics: Conference Series,
Vol. 980,
Issue. ,
p.
012002.
Naumov, I V
Glavny, V G
Sharifullin, B R
and
Shtern, V N
2018.
Multi-cellular pattern of a two-fluid swirling flow in a closed cylinder.
Journal of Physics: Conference Series,
Vol. 1105,
Issue. ,
p.
012030.
Naumov, Igor V.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2018.
Self-generation of cells in a two-fluid swirling flow.
Vol. 2027,
Issue. ,
p.
030069.
Carrión, Luis
Herrada, Miguel A.
and
Shtern, Vladimir N.
2018.
Stability of an air–water flow in a semispherical container.
European Journal of Mechanics - B/Fluids,
Vol. 67,
Issue. ,
p.
377.
Naumov, Igor V.
Herrada, Miguel A.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2018.
Slip at the interface of a two-fluid swirling flow.
Physics of Fluids,
Vol. 30,
Issue. 7,
Shtern, Vladimir
2018.
Mechanisms of jet instability: role of deceleration.
Fluid Dynamics Research,
Vol. 50,
Issue. 5,
p.
051408.
Naumov, Igor V.
Herrada, Miguel A.
Sharifullin, Bulat R.
and
Shtern, Vladimir N.
2018.
Hysteretic growth and decay of a waterspout column.
Physical Review Fluids,
Vol. 3,
Issue. 2,
Naumov, Igor V.
Tsoy, Mikhail
and
Sharifullin, Bulat
2019.
Experimentally investigating the instability onset in closed polygonal containers.
Experiments in Fluids,
Vol. 60,
Issue. 12,
Naumov, I V
Sharifullin, B R
and
Shtern, V N
2019.
Flow at the interface of two rotating fluids.
Journal of Physics: Conference Series,
Vol. 1382,
Issue. 1,
p.
012026.
Shtern, V N
2019.
Mechanism of counterflows and circulation cells in swirling flows.
Journal of Physics: Conference Series,
Vol. 1382,
Issue. 1,
p.
012041.
Naumov, I V
and
Tsoy, M A
2019.
Laser diagnostics of the instability onset in the confined vortex flows.
Journal of Physics: Conference Series,
Vol. 1421,
Issue. 1,
p.
012028.
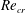 $\mathit{Re}_{cr}$
, is found to be nearly
$\mathit{Re}_{cr}$
, is found to be nearly
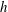 $h$
-independent for
$h$
-independent for
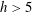 $h>5$
;
$h>5$
;
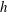 $h$
is the cylinder length-to-radius ratio. It is shown that the sidewall co-rotation suppresses the instability. As the co-rotation increases, the centrifugal instability becomes the most dangerous, i.e. determines
$h$
is the cylinder length-to-radius ratio. It is shown that the sidewall co-rotation suppresses the instability. As the co-rotation increases, the centrifugal instability becomes the most dangerous, i.e. determines
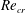 $\mathit{Re}_{cr}$
. Physical explanations are given for the stabilizing effect of the co-rotation, which is stronger (weaker) for the shear-layer (centrifugal) instability.
$\mathit{Re}_{cr}$
. Physical explanations are given for the stabilizing effect of the co-rotation, which is stronger (weaker) for the shear-layer (centrifugal) instability.


