Published online by Cambridge University Press: 20 February 2012
The Taylor–Goldstein (T–G) equation is extended to include the effects of small-scale turbulence represented by non-uniform vertical and horizontal eddy viscosity and diffusion coefficients. The vertical coefficients of viscosity and diffusion, 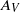 and
and 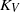 , respectively, are assumed to be equal and are expressed in terms of the buoyancy frequency of the flow,
, respectively, are assumed to be equal and are expressed in terms of the buoyancy frequency of the flow, 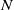 , and the dissipation rate of turbulent kinetic energy per unit mass,
, and the dissipation rate of turbulent kinetic energy per unit mass,  , quantities that can be measured in the sea. The horizontal eddy coefficients,
, quantities that can be measured in the sea. The horizontal eddy coefficients, 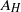 and
and 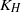 , are taken to be proportional to the dimensionally correct form,
, are taken to be proportional to the dimensionally correct form, 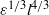 , found appropriate in the description of horizontal dispersion of a field of passive markers of scale
, found appropriate in the description of horizontal dispersion of a field of passive markers of scale 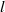 . The extended T–G equation is applied to examine the stability and greatest growth rates in a turbulent shear flow in stratified waters near a sill, that at the entrance to the Clyde Sea in the west of Scotland. Here the main effect of turbulence is a tendency towards stabilizing the flow; the greatest growth rates of small unstable disturbances decrease, and in some cases flows that are unstable in the absence of turbulence are stabilized when its effects are included. It is conjectured that stabilization of a flow by turbulence may lead to a repeating cycle in which a flow with low levels of turbulence becomes unstable, increasing the turbulent dissipation rate and so stabilizing the flow. The collapse of turbulence then leads to a condition in which the flow may again become unstable, the cycle repeating. Two parameters are used to describe the ‘marginality’ of the observed flows. One is based on the proximity of the minimum flow Richardson number to the critical Richardson number, the other on the change in dissipation rate required to stabilize or destabilize an observed flow. The latter is related to the change needed in the flow Reynolds number to achieve zero growth rate. The unstable flows, typical of the Clyde Sea site, are relatively further from neutral stability in Reynolds number than in Richardson number. The effects of turbulence on the hydraulic state of the flow are assessed by examining the speed and propagation direction of long waves in the Clyde Sea. Results are compared to those obtained using the T–G equation without turbulent viscosity or diffusivity. Turbulence may change the state of a flow from subcritical to supercritical.
. The extended T–G equation is applied to examine the stability and greatest growth rates in a turbulent shear flow in stratified waters near a sill, that at the entrance to the Clyde Sea in the west of Scotland. Here the main effect of turbulence is a tendency towards stabilizing the flow; the greatest growth rates of small unstable disturbances decrease, and in some cases flows that are unstable in the absence of turbulence are stabilized when its effects are included. It is conjectured that stabilization of a flow by turbulence may lead to a repeating cycle in which a flow with low levels of turbulence becomes unstable, increasing the turbulent dissipation rate and so stabilizing the flow. The collapse of turbulence then leads to a condition in which the flow may again become unstable, the cycle repeating. Two parameters are used to describe the ‘marginality’ of the observed flows. One is based on the proximity of the minimum flow Richardson number to the critical Richardson number, the other on the change in dissipation rate required to stabilize or destabilize an observed flow. The latter is related to the change needed in the flow Reynolds number to achieve zero growth rate. The unstable flows, typical of the Clyde Sea site, are relatively further from neutral stability in Reynolds number than in Richardson number. The effects of turbulence on the hydraulic state of the flow are assessed by examining the speed and propagation direction of long waves in the Clyde Sea. Results are compared to those obtained using the T–G equation without turbulent viscosity or diffusivity. Turbulence may change the state of a flow from subcritical to supercritical.