Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T16:45:21.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Insights into the dynamics of conical breakdown modes in coaxial swirling flow field

Published online by Cambridge University Press:  22 August 2018

Kuppuraj Rajamanickam  and
Saptarshi Basu Open the ORCID record for Saptarshi Basu [Opens in a new window]
Kuppuraj Rajamanickam
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore-560012, India
Saptarshi Basu*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore-560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main idea of this paper is to understand the fundamental vortex breakdown mechanisms in the coaxial swirling flow field. In particular, the interaction dynamics of the flow field is meticulously addressed with the help of high fidelity laser diagnostic tools. Time-resolved particle image velocimetry (PIV) (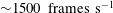${\sim}1500~\text{frames}~\text{s}^{-1}$) is employed in 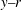$y{-}r$ and multiple 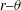$r{-}\unicode[STIX]{x1D703}$ planes to precisely delineate the flow dynamics. Experiments are carried out for three sets of co-annular flow Reynolds number 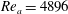$Re_{a}=4896$, 10 545, 17 546. Furthermore, for each 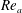$Re_{a}$ condition, the swirl number ‘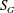$S_{G}$’ is varied independently from 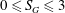$0\leqslant S_{G}\leqslant 3$. The global evolution of flow field across various swirl numbers is presented using the time-averaged PIV data. Three distinct forms of vortex breakdown namely, pre-vortex breakdown (PVB), central toroidal recirculation zone (CTRZ; axisymmetric toroidal bubble type breakdown) and sudden conical breakdown are witnessed. Among these, the conical form of vortex breakdown is less explored in the literature. In this paper, much attention is therefore focused on exploring the governing mechanism of conical breakdown. It is should be interesting to note that, unlike other vortex breakdown modes, conical breakdown persists only for a very short band of 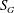$S_{G}$. For any small increase/decrease in 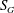$S_{G}$ beyond a certain threshold, the flow spontaneously reverts back to the CTRZ state. Energy ranked and frequency-resolved/ranked robust structure identification methods – proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD) respectively – are implemented over instantaneous time-resolved PIV data sets to extract the dynamics of the coherent structures associated with each vortex breakdown mode. The dominant structures obtained from POD analysis suggest the dominance of the Kelvin–Helmholtz (KH) instability (axial 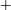$+$ azimuthal; accounts for 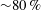${\sim}80\,\%$ of total turbulent kinetic energy, TKE) for both PVB and CTRZ while the remaining energy is contributed by shedding modes. On the other hand, shedding modes contribute the majority of the TKE in conical breakdown. The frequency signatures quantified from POD temporal modes and DMD analysis reveal the occurrence of multiple dominant frequencies in the range of 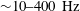${\sim}10{-}400~\text{Hz}$ with conical breakdown. This phenomenon may be a manifestation of high energy contribution by shedding eddies in the shear layer. Contrarily, with PVB and CTRZ, the dominant frequencies are observed in the range of 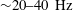${\sim}20{-}40~\text{Hz}$ only. We have provided a detailed exposition of the mechanism through which conical breakdown occurs. In addition, the current work explores the hysteresis (path dependence) phenomena of conical breakdown as functions of the Reynolds and Rossby numbers. It has been observed that the conical mode is not reversible and highly dependent on the initial conditions.

JFM classification

Vortex Flows: Vortex breakdown Vortex Flows: Vortex Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 853 , 25 October 2018 , pp. 72 - 110
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. & Peltier, W. R. 1998 Three-dimensional instability of anticyclonic swirling flow in rotating fluid: laboratory experiments and related theoretical predictions. Phys. Fluids 10, 3194–3202.Google Scholar
Arroyo, M. P. & Greated, C. A. 1991 Stereoscopic particle image velocimetry. Meas. Sci. Technol. 2, 1181–1186.Google Scholar
Benjamin, T. B. 1962 Theory of the vortex breakdown phenomenon. J. Fluid Mech. 14, 593–629.Google Scholar
Benjamin, T. B. 1967 Some developments in the theory of vortex breakdown. J. Fluid Mech. 28, 65–84.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.Google Scholar
Cala, C. E., Fernandes, Ec., Heitor, M. V. & Shtork, S. I. 2006 Coherent structures in unsteady swirling jet flow. Exp. Fluids 40, 267–276.Google Scholar
Cassidy, J. J. & Falvey, H. T. 1970 Observations of unsteady flow arising after vortex breakdown. J. Fluid Mech. 41, 727–736.Google Scholar
Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationships between local vortex identification schemes. J. Fluid Mech. 535, 189–214.Google Scholar
Chanaud, R. C. 1965 Observations of oscillatory motion in certain swirling flows. J. Fluid Mech. 21, 111–127.Google Scholar
Chterev, I., Sundararajan, G., Emerson, B., Seitzman, J. & Lieuwen, T. 2017 Precession effects on the relationship between time-averaged and instantaneous reacting flow characteristics. Combust. Sci. Technol. 189, 248–265.Google Scholar
Claypole, T. C. & Syred, N. 1981 The effect of swirl burner aerodynamics on NOx formation. In Symposium (International) on Combustion, pp. 81–89. Elsevier.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Escudier, M. P. & Keller, J. J. 1985 Recirculation in swirling flow – a manifestation of vortex breakdown. AIAA J. 23, 111–116.Google Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20, 1385–1400.Google Scholar
Fu, Y., Cai, J., Jeng, S.-M. & Mongia, H. 2007 Characteristics of the swirling flow generated by a counter-rotating swirler. In 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, p. 5690. AIAA.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003a Instability mechanisms in swirling flows. Phys. Fluids 15, 2622–2639.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003b Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.Google Scholar
Garcia-Villalba, M., Frohlich, J. & Rodi, W. 2005 Large eddy simulation of an annular swirling jet with pulsating inflow. In TSFP Digital Library Online. Begel House Inc.Google Scholar
Gupta, A. K., Lilley, D. G. & Syred, N. 1984 Swirl Flows, vol. 488, p. 1. Abacus Press.Google Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4, 195–218.Google Scholar
Harvey, J. K. 1962 Some observations of the vortex breakdown phenomenon. J. Fluid Mech. 14, 585–592.Google Scholar
Huang, Y., Wang, S. & Yang, V. 2005 Flow and flame dynamics of lean premixed swirl injectors. Prog. Astronaut. Aeronaut. 210, 213.Google Scholar
Komarek, T. & Polifke, W. 2010 Impact of swirl fluctuations on the flame response of a perfectly premixed swirl burner. Trans. ASME J. Engng Gas Turbines Power 132, 061503.Google Scholar
Lefebvre, A. H. 1998 Gas Turbine Combustion. CRC Press.Google Scholar
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.Google Scholar
Lieuwen, T. C. 2012 Unsteady Combustor Physics. Cambridge University Press.Google Scholar
Loiseleux, T., Chomaz, J. M. & Huerre, P. 1998 The effect of swirl on jets and wakes: linear instability of the Rankine vortex with axial flow. Phys. Fluids 10, 1120–1134.Google Scholar
Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 1. Confined swirling flow. J. Fluid Mech. 221, 533–552.Google Scholar
Lucca-Negro, O. & O’doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27, 431–481.Google Scholar
Markovich, D. M., Abdurakipov, S. S., Chikishev, L. M., Dulin, V. M. & Hanjalić, K. 2014 Comparative analysis of low-and high-swirl confined flames and jets by proper orthogonal and dynamic mode decompositions. Phys. Fluids 26, 065109.Google Scholar
Markovich, D. M., Dulin, V. M., Abdurakipov, S. S., Kozinkin, L. A., Tokarev, M. P. & Hanjalić, K. 2016 Helical modes in low-and high-swirl jets measured by tomographic PIV. J. Turbul. 17, 678–698.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.Google Scholar
Mohan, A. T., Gaitonde, D. V. & Visbal, M. R. 2015 Model reduction and analysis of deep dynamic stall on a plunging airfoil using dynamic mode decomposition. In 53rd AIAA Aerospace Sciences Meeting, p. 1058. AIAA.Google Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.Google Scholar
Oberleithner, K., Stöhr, M., Im, S. H., Arndt, C. M. & Steinberg, A. M. 2015 Formation and flame-induced suppression of the precessing vortex core in a swirl combustor: experiments and linear stability analysis. Combust. Flame 162, 3100–3114.Google Scholar
Prasad, A. K. & Adrian, R. J. 1993 Stereoscopic particle image velocimetry applied to liquid flows. Exp. Fluids 15, 49–60.Google Scholar
Proctor, J. L., Brunton, S. L. & Kutz, J. N. 2016 Dynamic mode decomposition with control. SIAM J. Appl. Dyn. Syst. 15, 142–161.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2013 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Rajamanickam, K. & Basu, S. 2017a On the dynamics of vortex–droplet interactions, dispersion and breakup in a coaxial swirling flow. J. Fluid Mech. 827, 572–613.Google Scholar
Rajamanickam, K. & Basu, S. 2017b Insights into the dynamics of spray–swirl interactions. J. Fluid Mech. 810, 82–126.Google Scholar
Rajamanickam, K., Roy, S. & Basu, S. 2018 Novel fuel injection systems for high-speed combustors. In Droplets and Sprays, pp. 183–216. Springer.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Roy, S., Yi, T., Jiang, N., Gunaratne, G. H., Chterev, I., Emerson, B., Lieuwen, T., Caswell, A. W. & Gord, J. R. 2017 Dynamics of robust structures in turbulent swirling reacting flows. J. Fluid Mech. 816, 554–585.Google Scholar
Santhosh, R. & Basu, S. 2015 Acoustic response of vortex breakdown modes in a coaxial isothermal unconfined swirling jet. Phys. Fluids 27, 033601.Google Scholar
Santhosh, R., Miglani, A. & Basu, S. 2013 Transition and acoustic response of recirculation structures in an unconfined co-axial isothermal swirling flow. Phys. Fluids 25, 083603.Google Scholar
Santhosh, R., Miglani, A. & Basu, S. 2014 Transition in vortex breakdown modes in a coaxial isothermal unconfined swirling jet. Phys. Fluids 26, 043601.Google Scholar
Sarpkaya, T. 1971a Vortex breakdown in swirling conical flows. AIAA J. 9, 1792–1799.Google Scholar
Sarpkaya, T. 1971b On stationary and travelling vortex breakdowns. J. Fluid Mech. 45, 545–559.Google Scholar
Sarpkaya, T. 1974 Effect of the adverse pressure gradient on vortex breakdown. AIAA J. 12, 602–607.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sciacchitano, A., Wieneke, B. & Scarano, F. 2013 PIV uncertainty quantification by image matching. Meas. Sci. Technol. 24, 045302.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I. Coherent structures. Q. Appl. Maths 45, 561–571.Google Scholar
Spall, R. E., Gatski, T. B. & Grosch, C. E. 1987 A criterion for vortex breakdown. Phys. Fluids 30, 3434–3440.Google Scholar
Steinberg, A. M., Boxx, I., Stöhr, M., Meier, W. & Carter, C. D. 2012 Effects of flow structure dynamics on thermoacoustic instabilities in swirl-stabilized combustion. AIAA J. 50, 952–967.Google Scholar
Stöhr, M., Arndt, C. M. & Meier, W. 2013 Effects of Damköhler number on vortex–flame interaction in a gas turbine model combustor. Proc. Combust. Inst. 34, 3107–3115.Google Scholar
Stöhr, M., Arndt, C. M. & Meier, W. 2015 Transient effects of fuel–air mixing in a partially-premixed turbulent swirl flame. Proc. Combust. Inst. 35, 3327–3335.Google Scholar
Syred, N. 2006 A review of oscillation mechanisms and the role of the precessing vortex core (PVC) in swirl combustion systems. Prog. Energy Combust. Sci. 32, 93–161.Google Scholar
Taira, K., Brunton, S. L., Dawson, S., Rowley, C. W., Colonius, T., McKeon, B. J., Schmidt, O. T., Gordeyev, S., Theofilis, V. & Ukeiley, L. S.2017 Modal analysis of fluid flows: an overview. arXiv:1702.01453.Google Scholar
Wang, S., Rusak, Z., Gong, R. & Liu, F. 2016 On the three-dimensional stability of a solid-body rotation flow in a finite-length rotating pipe. J. Fluid Mech. 797, 284–321.Google Scholar
Wieneke, B. 2015 PIV uncertainty quantification from correlation statistics. Meas. Sci. Technol. 26, 074002.Google Scholar
Williams, M. O., Kevrekidis, I. G. & Rowley, C. W. 2015 A data-driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346.Google Scholar
Wilson, B. M., Mejia-Alvarez, R. & Prestridge, K. 2015 Simultaneous PIV and PLIF measurements of Mach number effects on single-interface Richtmyer–Meshkov mixing. In 29th International Symposium on Shock Waves 2, pp. 1125–1130. Springer.Google Scholar

Rajamanickam et al. supplementary movie 1

Flow transitions to CB

Download Rajamanickam et al. supplementary movie 1(Video)
Video 52.6 MB

Rajamanickam et al. supplementary movie 2

Flow structures in r-theta plane

Download Rajamanickam et al. supplementary movie 2(Video)
Video 9.4 MB

Rajamanickam et al. supplementary movie 3

Intense outer shear layer shedding for PVB

Download Rajamanickam et al. supplementary movie 3(Video)
Video 5.3 MB

Rajamanickam et al. supplementary movie 4

Different transitions

Download Rajamanickam et al. supplementary movie 4(Video)
Video 23.3 MB

Rajamanickam et al. supplementary movie 5

Full conical breakdown in yr plane

Download Rajamanickam et al. supplementary movie 5(Video)
Video 37.6 MB

Rajamanickam et al. supplementary movie 6

The full spectrum of flow structures

Download Rajamanickam et al. supplementary movie 6(Video)
Video 9.9 MB