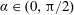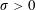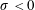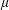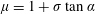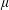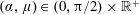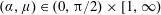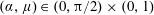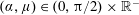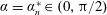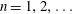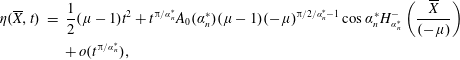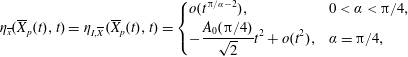1 Introduction
The two-dimensional (2D) irrotational flow generated by the steadily accelerating motion of a flat rigid plate inclined at an angle
![]() $\unicode[STIX]{x1D6FC}$
to the horizontal into a uniform horizontal strip of inviscid fluid under the action of gravity has previously been studied, with the small-time structure investigated in detail by King & Needham (Reference King and Needham1994), Needham, Billingham & King (Reference Needham, Billingham and King2007) and Needham, Chamberlain & Billingham (Reference Needham, Chamberlain and Billingham2008), and, subsequently, the large-time structure investigated in Needham (Reference Needham2012). In each of the small-time studies, it was found that a jet rises up the surface of the plate, close to the initial intersection point of the free surface and the plate. In addition to the abovementioned series of papers, there have been a number of studies (both experimental and numerical) by other authors on related problems. Greenhow & Lin (Reference Greenhow and Lin1983) performed a series of scale-model experiments involving the impulsive start of a wavemaker, and the high-speed entry of a wedge into calm water. Yang & Chwang (Reference Yang and Chwang1992) investigated the case of a surface piercing vertical plate impulsively accelerated into an expanse of initially stationary fluid. Their scale-model experiments found that water rises up the plate during the initial stages of plate motion, in good agreement with the numerical solutions found by Yang & Chwang (Reference Yang and Chwang1989). There have been several studies concerning the family of water-entry problems, which are closely linked to the topic of this paper. A review of incompressible water-entry problems characterised by the impacting body being nearly parallel to the initially flat water surface was presented by Howison, Ockendon & Wilson (Reference Howison, Ockendon and Wilson1991). Similar methods to those applied in the current paper have been employed by Iafrati & Korobkin (Reference Iafrati and Korobkin2005) and Tassin, Korobkin & Cooker (Reference Tassin, Korobkin and Cooker2014), who considered the problem of flow generated by the impulsive start of a floating wedge. Greenhow (Reference Greenhow1987) conducted a numerical investigation into the wedge entry problem. He found that a jet of fluid rises up the side of the wedge and may then separate from the wedge surface, which agrees qualitatively with the experiments of Greenhow & Lin (Reference Greenhow and Lin1983). This behaviour is not fully explained, but it was suggested by the author that there is an introduction of new free surface particles between the original intersection between the surface of the wedge and the tip of the jet, with a modified numerical scheme achieving some success in simulating such flows. Other small-time free surface problems include that of modelling the initial stages of dam-break problems. Yilmaz, Korobkin & Iafrati (Reference Yilmaz, Korobkin and Iafrati2013) studied the dam-break problem for two immiscible fluids. Here, the authors paid close attention to the motion at the point at which the free surfaces of the fluids and the interface meet. The singularity of the flow at this point was shown to be dependent on the density ratio between the two fluids, and the shape of the flow region. The fine details of the flow near this point were investigated by the introduction of an inner region that contained the intersection point between the free surfaces of the fluid and the interface.
$\unicode[STIX]{x1D6FC}$
to the horizontal into a uniform horizontal strip of inviscid fluid under the action of gravity has previously been studied, with the small-time structure investigated in detail by King & Needham (Reference King and Needham1994), Needham, Billingham & King (Reference Needham, Billingham and King2007) and Needham, Chamberlain & Billingham (Reference Needham, Chamberlain and Billingham2008), and, subsequently, the large-time structure investigated in Needham (Reference Needham2012). In each of the small-time studies, it was found that a jet rises up the surface of the plate, close to the initial intersection point of the free surface and the plate. In addition to the abovementioned series of papers, there have been a number of studies (both experimental and numerical) by other authors on related problems. Greenhow & Lin (Reference Greenhow and Lin1983) performed a series of scale-model experiments involving the impulsive start of a wavemaker, and the high-speed entry of a wedge into calm water. Yang & Chwang (Reference Yang and Chwang1992) investigated the case of a surface piercing vertical plate impulsively accelerated into an expanse of initially stationary fluid. Their scale-model experiments found that water rises up the plate during the initial stages of plate motion, in good agreement with the numerical solutions found by Yang & Chwang (Reference Yang and Chwang1989). There have been several studies concerning the family of water-entry problems, which are closely linked to the topic of this paper. A review of incompressible water-entry problems characterised by the impacting body being nearly parallel to the initially flat water surface was presented by Howison, Ockendon & Wilson (Reference Howison, Ockendon and Wilson1991). Similar methods to those applied in the current paper have been employed by Iafrati & Korobkin (Reference Iafrati and Korobkin2005) and Tassin, Korobkin & Cooker (Reference Tassin, Korobkin and Cooker2014), who considered the problem of flow generated by the impulsive start of a floating wedge. Greenhow (Reference Greenhow1987) conducted a numerical investigation into the wedge entry problem. He found that a jet of fluid rises up the side of the wedge and may then separate from the wedge surface, which agrees qualitatively with the experiments of Greenhow & Lin (Reference Greenhow and Lin1983). This behaviour is not fully explained, but it was suggested by the author that there is an introduction of new free surface particles between the original intersection between the surface of the wedge and the tip of the jet, with a modified numerical scheme achieving some success in simulating such flows. Other small-time free surface problems include that of modelling the initial stages of dam-break problems. Yilmaz, Korobkin & Iafrati (Reference Yilmaz, Korobkin and Iafrati2013) studied the dam-break problem for two immiscible fluids. Here, the authors paid close attention to the motion at the point at which the free surfaces of the fluids and the interface meet. The singularity of the flow at this point was shown to be dependent on the density ratio between the two fluids, and the shape of the flow region. The fine details of the flow near this point were investigated by the introduction of an inner region that contained the intersection point between the free surfaces of the fluid and the interface.
In this paper, we generalise the work presented in Needham et al. (Reference Needham, Chamberlain and Billingham2008), for an advancing plate, to the case of a plate, inclined at an angle
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, advancing into or retreating away from an inviscid irrotational fluid, with constant acceleration
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, advancing into or retreating away from an inviscid irrotational fluid, with constant acceleration
![]() $a\in \mathbb{R}$
(see figure 1). We consider again the case of advancing plates both for completeness and because we are able to remove the dependence on acceleration from the problem by utilising an observation that was overlooked in Needham et al. (Reference Needham, Chamberlain and Billingham2008). The case of the retreating plate is then considered in detail. We use the method of matched asymptotic expansions to investigate the asymptotic structure of the solution to the free surface evolution problem in the small-time limit, where we are particularly interested in the behaviour of the free surface in the innermost asymptotic region close to the contact point between the plate and the free surface. The structure of the solution to this problem is interpreted in terms of the parameters
$a\in \mathbb{R}$
(see figure 1). We consider again the case of advancing plates both for completeness and because we are able to remove the dependence on acceleration from the problem by utilising an observation that was overlooked in Needham et al. (Reference Needham, Chamberlain and Billingham2008). The case of the retreating plate is then considered in detail. We use the method of matched asymptotic expansions to investigate the asymptotic structure of the solution to the free surface evolution problem in the small-time limit, where we are particularly interested in the behaviour of the free surface in the innermost asymptotic region close to the contact point between the plate and the free surface. The structure of the solution to this problem is interpreted in terms of the parameters
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
and
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
and
![]() $\unicode[STIX]{x1D707}\in \mathbb{R}$
(where
$\unicode[STIX]{x1D707}\in \mathbb{R}$
(where
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D70E}$
being the dimensionless acceleration), with a change of structure as
$\unicode[STIX]{x1D70E}$
being the dimensionless acceleration), with a change of structure as
![]() $\unicode[STIX]{x1D707}$
changes sign. When
$\unicode[STIX]{x1D707}$
changes sign. When
![]() $\unicode[STIX]{x1D707}<0$
, with
$\unicode[STIX]{x1D707}<0$
, with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, we find a particularly delicate structure, with a sequence of pairs of near resonance points between which the initial gradient of the free surface rapidly changes sign, vanishing at a sequence of points
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, we find a particularly delicate structure, with a sequence of pairs of near resonance points between which the initial gradient of the free surface rapidly changes sign, vanishing at a sequence of points
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
) which are decreasing in
$n=1,2,\ldots$
) which are decreasing in
![]() $n$
and approach zero as
$n$
and approach zero as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
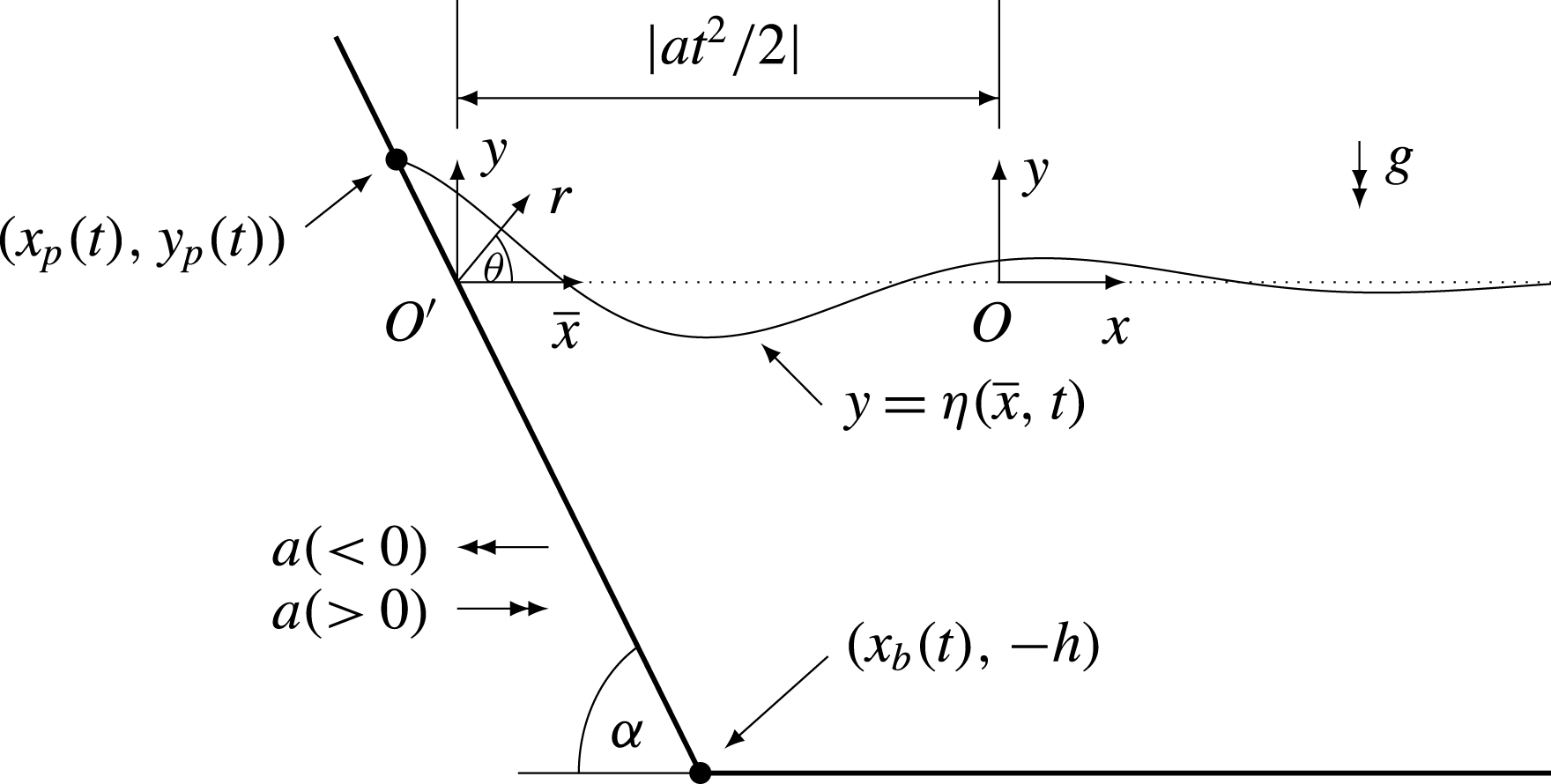
Figure 1. Definition sketch showing the displacement of the plate and free surface at time
![]() $t$
.
$t$
.
The outline of this paper is as follows. In § 2, we formulate the mathematical problem (which we term [IBVP]) via the governing hydrodynamic equations along with the associated boundary and initial conditions, and regularity requirements. Following the method of matched asymptotic expansions, §§ 3 and 4 consider the solutions to [IBVP] as time
![]() $t\rightarrow 0^{+}$
in the outer and inner asymptotic regions respectively. Finally, the case
$t\rightarrow 0^{+}$
in the outer and inner asymptotic regions respectively. Finally, the case
![]() $\unicode[STIX]{x1D707}=0$
requires that we consider an inner–inner asymptotic region, which is discussed in § 5. In § 6, we draw conclusions on both the mathematical and fluid mechanical implications of this work, and motivate the analysis in the companion paper, Gallagher, Needham & Billingham (Reference Gallagher, Needham and Billingham2018).
$\unicode[STIX]{x1D707}=0$
requires that we consider an inner–inner asymptotic region, which is discussed in § 5. In § 6, we draw conclusions on both the mathematical and fluid mechanical implications of this work, and motivate the analysis in the companion paper, Gallagher, Needham & Billingham (Reference Gallagher, Needham and Billingham2018).
2 Equations of motion
We consider the situation where, initially at time
![]() $t=0$
, a semi-infinite strip of inviscid incompressible fluid under the action of gravity lies at rest above a plane horizontal bed at
$t=0$
, a semi-infinite strip of inviscid incompressible fluid under the action of gravity lies at rest above a plane horizontal bed at
![]() $y=-h$
and is bounded above by its horizontal free surface at
$y=-h$
and is bounded above by its horizontal free surface at
![]() $y=0$
. Here,
$y=0$
. Here,
![]() $(x,y)$
denotes the Cartesian coordinate system fixed in space, with
$(x,y)$
denotes the Cartesian coordinate system fixed in space, with
![]() $x$
pointing horizontally into the fluid layer and
$x$
pointing horizontally into the fluid layer and
![]() $y$
pointing vertically upward. The fluid layer is initially bounded on the left by an inclined rigid plate at
$y$
pointing vertically upward. The fluid layer is initially bounded on the left by an inclined rigid plate at
![]() $y=-x\tan \unicode[STIX]{x1D6FC}$
, with
$y=-x\tan \unicode[STIX]{x1D6FC}$
, with
![]() $\unicode[STIX]{x1D6FC}$
being the angle of inclination of the plate with the negative
$\unicode[STIX]{x1D6FC}$
being the angle of inclination of the plate with the negative
![]() $x$
-axis. From
$x$
-axis. From
![]() $t=0$
, the plate translates in the
$t=0$
, the plate translates in the
![]() $x$
direction with constant acceleration
$x$
direction with constant acceleration
![]() $a\in \mathbb{R}$
. The free surface of the fluid is subsequently located at
$a\in \mathbb{R}$
. The free surface of the fluid is subsequently located at
![]() $y=\unicode[STIX]{x1D702}(x,t)$
, with the contact point between the free surface of the fluid and the inclined plate denoted by
$y=\unicode[STIX]{x1D702}(x,t)$
, with the contact point between the free surface of the fluid and the inclined plate denoted by
![]() $(x,y)=(x_{p}(t),y_{p}(t))$
, with
$(x,y)=(x_{p}(t),y_{p}(t))$
, with
![]() $y_{p}(t)=\unicode[STIX]{x1D702}(x_{p}(t),t)$
. In addition, the intersection point of the inclined plate and the rigid bed is denoted by
$y_{p}(t)=\unicode[STIX]{x1D702}(x_{p}(t),t)$
. In addition, the intersection point of the inclined plate and the rigid bed is denoted by
![]() $(x,y)=(x_{b}(t),-h)$
. The situation is illustrated in figure 1. In this paper, we consider the situation with
$(x,y)=(x_{b}(t),-h)$
. The situation is illustrated in figure 1. In this paper, we consider the situation with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. The fluid motion when
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. The fluid motion when
![]() $t>0$
is irrotational, since the fluid is initially at rest, and hence there exists a velocity potential
$t>0$
is irrotational, since the fluid is initially at rest, and hence there exists a velocity potential
![]() $\unicode[STIX]{x1D719}(x,y,t)$
. In addition, we denote the fluid pressure by
$\unicode[STIX]{x1D719}(x,y,t)$
. In addition, we denote the fluid pressure by
![]() $p(x,y,t)$
, and introduce dimensionless variables
$p(x,y,t)$
, and introduce dimensionless variables
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x^{\prime }=\frac{x}{h},\quad y^{\prime }=\frac{y}{h},\quad \unicode[STIX]{x1D702}^{\prime }=\frac{\unicode[STIX]{x1D702}}{h},\\ \displaystyle \unicode[STIX]{x1D719}^{\prime }=\frac{\unicode[STIX]{x1D719}}{h\sqrt{gh}},\quad p^{\prime }=\frac{p}{\unicode[STIX]{x1D70C}gh},\quad t^{\prime }=t\sqrt{\frac{g}{h}},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle x^{\prime }=\frac{x}{h},\quad y^{\prime }=\frac{y}{h},\quad \unicode[STIX]{x1D702}^{\prime }=\frac{\unicode[STIX]{x1D702}}{h},\\ \displaystyle \unicode[STIX]{x1D719}^{\prime }=\frac{\unicode[STIX]{x1D719}}{h\sqrt{gh}},\quad p^{\prime }=\frac{p}{\unicode[STIX]{x1D70C}gh},\quad t^{\prime }=t\sqrt{\frac{g}{h}},\end{array}\right\}\end{eqnarray}$$
and set
with
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $g$
and
$g$
and
![]() $\unicode[STIX]{x1D70C}$
being the dimensionless plate acceleration, the acceleration due to gravity and the density of the fluid respectively. Hereafter, we drop the primes for ease of notation. It is convenient to introduce the coordinate
$\unicode[STIX]{x1D70C}$
being the dimensionless plate acceleration, the acceleration due to gravity and the density of the fluid respectively. Hereafter, we drop the primes for ease of notation. It is convenient to introduce the coordinate
![]() $\overline{x}$
, defined by
$\overline{x}$
, defined by
![]() $\overline{x}=x-s(t)$
in
$\overline{x}=x-s(t)$
in
![]() $t\geqslant 0$
, where
$t\geqslant 0$
, where
with
![]() $s(t)$
measuring the displacement of the intersection point of the plate and the positive
$s(t)$
measuring the displacement of the intersection point of the plate and the positive
![]() $x$
-axis from the fixed origin in the
$x$
-axis from the fixed origin in the
![]() $(x,y)$
plane. The origin
$(x,y)$
plane. The origin
![]() $O^{\prime }$
of the
$O^{\prime }$
of the
![]() $(\overline{x},y)$
Cartesian coordinate system is now located on the plate. The
$(\overline{x},y)$
Cartesian coordinate system is now located on the plate. The
![]() $(\overline{x},y)$
Cartesian coordinate system will be the primary coordinate system throughout the paper. We now define the domain occupied by the fluid in the
$(\overline{x},y)$
Cartesian coordinate system will be the primary coordinate system throughout the paper. We now define the domain occupied by the fluid in the
![]() $(\overline{x},y)$
plane to be given, at each
$(\overline{x},y)$
plane to be given, at each
![]() $t\geqslant 0$
, by
$t\geqslant 0$
, by
![]() ${\mathcal{D}}(t)={\mathcal{D}}_{1}(t)\cup {\mathcal{D}}_{2}(t)$
, with
${\mathcal{D}}(t)={\mathcal{D}}_{1}(t)\cup {\mathcal{D}}_{2}(t)$
, with
where
![]() $\overline{x}_{p}(t)=x_{p}(t)-s(t)$
,
$\overline{x}_{p}(t)=x_{p}(t)-s(t)$
,
![]() $\overline{x}_{b}=\cot \unicode[STIX]{x1D6FC}$
, with now
$\overline{x}_{b}=\cot \unicode[STIX]{x1D6FC}$
, with now
![]() $y_{p}(t)=\unicode[STIX]{x1D702}(\overline{x}_{p}(t),t)=-\overline{x}_{p}(t)\tan \unicode[STIX]{x1D6FC}$
in
$y_{p}(t)=\unicode[STIX]{x1D702}(\overline{x}_{p}(t),t)=-\overline{x}_{p}(t)\tan \unicode[STIX]{x1D6FC}$
in
![]() $t\geqslant 0$
.
$t\geqslant 0$
.
The governing equations and boundary conditions are
Here,
![]() $\unicode[STIX]{x1D735}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$
, and
$\unicode[STIX]{x1D735}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)$
, and
![]() $\hat{\boldsymbol{n}}=(\sin \unicode[STIX]{x1D6FC},\cos \unicode[STIX]{x1D6FC})$
is the unit normal to the plate pointing into the fluid. In addition to (2.5)–(2.11), we have the initial conditions
$\hat{\boldsymbol{n}}=(\sin \unicode[STIX]{x1D6FC},\cos \unicode[STIX]{x1D6FC})$
is the unit normal to the plate pointing into the fluid. In addition to (2.5)–(2.11), we have the initial conditions
The pressure field (setting atmospheric pressure to zero) is given explicitly by
with
![]() $p_{d}$
being the dynamic fluid pressure field, which is given, via the Bernoulli equation, by
$p_{d}$
being the dynamic fluid pressure field, which is given, via the Bernoulli equation, by
We will study classical solutions to the initial boundary value problem (2.5)–(2.13) (excluding contact point separation or cavitation), in the sense that we require the regularity conditions
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\mathcal{G}}=\{(\overline{x},y,t)\in \mathbb{R}^{3}:(\overline{x},y)\in {\mathcal{D}}(t),\quad t\in (0,\infty )\},\\ \unicode[STIX]{x2202}{\mathcal{G}}=\{(\overline{x},y,t)\in \mathbb{R}^{3}:(\overline{x},y)\in \overline{{\mathcal{D}}}(t)\backslash {\mathcal{D}}(t),\quad t\in (0,\infty )\},\\ {\mathcal{H}}=\{(\overline{x},t)\in {\mathcal{R}}^{2}:\overline{x}\in [\overline{x}_{p}(t),\infty ),\quad t\in (0,\infty )\}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}{\mathcal{G}}=\{(\overline{x},y,t)\in \mathbb{R}^{3}:(\overline{x},y)\in {\mathcal{D}}(t),\quad t\in (0,\infty )\},\\ \unicode[STIX]{x2202}{\mathcal{G}}=\{(\overline{x},y,t)\in \mathbb{R}^{3}:(\overline{x},y)\in \overline{{\mathcal{D}}}(t)\backslash {\mathcal{D}}(t),\quad t\in (0,\infty )\},\\ {\mathcal{H}}=\{(\overline{x},t)\in {\mathcal{R}}^{2}:\overline{x}\in [\overline{x}_{p}(t),\infty ),\quad t\in (0,\infty )\}.\end{array}\right\}\end{eqnarray}$$
These regularity conditions, particularly with regard to the free surface and plate contact point, are the minimal conditions for classical smoothness at the contact point in
![]() $t\geqslant 0$
, requiring finite fluid velocity, finite contact point velocity and finite free surface slope at the contact point in
$t\geqslant 0$
, requiring finite fluid velocity, finite contact point velocity and finite free surface slope at the contact point in
![]() $t\geqslant 0$
. They are required to eliminate eigensolutions with singular fluid velocities and free surface slope in the outer region, as discussed in § 3, after (3.4), and in the inner region, as discussed in § 4.2, from (4.26) to (4.29) and in the paragraph before (4.36). We will henceforth refer to the initial boundary value problem (2.5)–(2.13), with regularity conditions (2.16), as [IBVP]. The purpose of this paper is to investigate the principal flow through construction of the asymptotic structure of the solution to [IBVP] as
$t\geqslant 0$
. They are required to eliminate eigensolutions with singular fluid velocities and free surface slope in the outer region, as discussed in § 3, after (3.4), and in the inner region, as discussed in § 4.2, from (4.26) to (4.29) and in the paragraph before (4.36). We will henceforth refer to the initial boundary value problem (2.5)–(2.13), with regularity conditions (2.16), as [IBVP]. The purpose of this paper is to investigate the principal flow through construction of the asymptotic structure of the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
via the method of matched asymptotic expansions.
$t\rightarrow 0^{+}$
via the method of matched asymptotic expansions.
We should remark here that when
![]() $\unicode[STIX]{x1D70E}<0$
, the initial boundary value problem [IBVP] represents a principal flow that is a boundary withdrawal problem under gravity, adjacent to a free surface. By imposing the regularity conditions (2.16), we are explicitly examining the existence of solutions to [IBVP], in which the motion of the contact point
$\unicode[STIX]{x1D70E}<0$
, the initial boundary value problem [IBVP] represents a principal flow that is a boundary withdrawal problem under gravity, adjacent to a free surface. By imposing the regularity conditions (2.16), we are explicitly examining the existence of solutions to [IBVP], in which the motion of the contact point
![]() $(x_{p}(t),-x_{p}(t)\tan \unicode[STIX]{x1D6FC})$
remains regular in
$(x_{p}(t),-x_{p}(t)\tan \unicode[STIX]{x1D6FC})$
remains regular in
![]() $t\geqslant 0$
; that is, no separation occurs at
$t\geqslant 0$
; that is, no separation occurs at
![]() $t=0^{+}$
of the initial contact point, at
$t=0^{+}$
of the initial contact point, at
![]() $(\overline{x},y)=(0,0)$
, from the plate. Indeed, the occurrence of such a separation would require a singularity formation in the dynamic pressure
$(\overline{x},y)=(0,0)$
, from the plate. Indeed, the occurrence of such a separation would require a singularity formation in the dynamic pressure
![]() $p_{d}$
(in (2.15)) at
$p_{d}$
(in (2.15)) at
![]() $(x,y)=(0,0)$
when
$(x,y)=(0,0)$
when
![]() $t=0^{+}$
, which would then be alleviated by separation when
$t=0^{+}$
, which would then be alleviated by separation when
![]() $t>0^{+}$
. However, within the framework of matched asymptotic expansions, we demonstrate that the solution to [IBVP] has
$t>0^{+}$
. However, within the framework of matched asymptotic expansions, we demonstrate that the solution to [IBVP] has
![]() $p_{d}$
regular at
$p_{d}$
regular at
![]() $(\overline{x},y)=(0,0)$
when
$(\overline{x},y)=(0,0)$
when
![]() $t=0^{+}$
, and thus contact point separation does not occur at
$t=0^{+}$
, and thus contact point separation does not occur at
![]() $t=0^{+}$
. In contrast, we observe that in the related problem, when the plate is extracted from the fluid layer with an initial finite impulsive velocity, the impulsively induced pressure field at
$t=0^{+}$
. In contrast, we observe that in the related problem, when the plate is extracted from the fluid layer with an initial finite impulsive velocity, the impulsively induced pressure field at
![]() $t=0^{+}$
, in the corresponding formulation to [IBVP], does have a singularity at
$t=0^{+}$
, in the corresponding formulation to [IBVP], does have a singularity at
![]() $(\overline{x},y)=(0,0)$
when
$(\overline{x},y)=(0,0)$
when
![]() $t=0^{+}$
, and separation should be anticipated. Indeed, this behaviour has been reported in a corresponding impulsive extraction problem in Norkin & Korobkin (Reference Norkin and Korobkin2011), with a similar forward impulsive problem examined in Needham et al. (Reference Needham, Billingham and King2007). In addition, we should also remark that although contact point separation does not occur in the principal flow determined by [IBVP], it is certainly possible that this principal flow, close to the initial contact point, may be temporally unstable, and even ill-posed, to small initial perturbations, and that subsequent rapid growth in local perturbations close to the initial contact point could lead to subsequent contact point separation. Indeed, it is this question that is addressed in part 2 of this pair of papers (Gallagher et al.
Reference Gallagher, Needham and Billingham2018). Additional discussion is given in Sedov et al. (Reference Sedov, Chu, C, Seckler and Gillis1965).
$t=0^{+}$
, and separation should be anticipated. Indeed, this behaviour has been reported in a corresponding impulsive extraction problem in Norkin & Korobkin (Reference Norkin and Korobkin2011), with a similar forward impulsive problem examined in Needham et al. (Reference Needham, Billingham and King2007). In addition, we should also remark that although contact point separation does not occur in the principal flow determined by [IBVP], it is certainly possible that this principal flow, close to the initial contact point, may be temporally unstable, and even ill-posed, to small initial perturbations, and that subsequent rapid growth in local perturbations close to the initial contact point could lead to subsequent contact point separation. Indeed, it is this question that is addressed in part 2 of this pair of papers (Gallagher et al.
Reference Gallagher, Needham and Billingham2018). Additional discussion is given in Sedov et al. (Reference Sedov, Chu, C, Seckler and Gillis1965).
Finally, we note here that throughout the paper, to reduce the need for additional notation (in the already extensive notation required), we adopt the convention that the principal dependent variables that appear in both inner and outer regions, for example the velocity potential
![]() $\unicode[STIX]{x1D719}$
and the free surface displacement
$\unicode[STIX]{x1D719}$
and the free surface displacement
![]() $\unicode[STIX]{x1D702}$
, will be assumed to have spatial arguments associated with the region and coordinate system under consideration at that stage. For example,
$\unicode[STIX]{x1D702}$
, will be assumed to have spatial arguments associated with the region and coordinate system under consideration at that stage. For example,
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}(\cdot ,\cdot ,t)$
and
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}(\cdot ,\cdot ,t)$
and
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\cdot ,t)$
, where, considering the outer region,
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}(\cdot ,t)$
, where, considering the outer region,
![]() $(\cdot ,\cdot ,t)=(x,y,t)$
and
$(\cdot ,\cdot ,t)=(x,y,t)$
and
![]() $(\cdot ,t)=(x,t)$
when working in the outer region Cartesian coordinates
$(\cdot ,t)=(x,t)$
when working in the outer region Cartesian coordinates
![]() $(x,y)$
, while
$(x,y)$
, while
![]() $(\cdot ,\cdot ,t)=(r,\unicode[STIX]{x1D703},t)$
and
$(\cdot ,\cdot ,t)=(r,\unicode[STIX]{x1D703},t)$
and
![]() $(\cdot ,t)=(r,t)$
when working in the outer region polar coordinates
$(\cdot ,t)=(r,t)$
when working in the outer region polar coordinates
![]() $(r,\unicode[STIX]{x1D703})$
. Similarly, in the inner region,
$(r,\unicode[STIX]{x1D703})$
. Similarly, in the inner region,
![]() $(\cdot ,\cdot ,t)=(X,Y,t)$
and
$(\cdot ,\cdot ,t)=(X,Y,t)$
and
![]() $(\cdot ,t)=(X,t)$
, or
$(\cdot ,t)=(X,t)$
, or
![]() $(\cdot ,\cdot ,t)=(\overline{X},\overline{Y},t)$
and
$(\cdot ,\cdot ,t)=(\overline{X},\overline{Y},t)$
and
![]() $(\cdot ,t)=(\overline{X},t)$
when working in the inner region Cartesian coordinates
$(\cdot ,t)=(\overline{X},t)$
when working in the inner region Cartesian coordinates
![]() $(X,Y)$
or
$(X,Y)$
or
![]() $(\bar{X},\bar{Y})$
, with a similar convention when working in the inner region polar coordinates
$(\bar{X},\bar{Y})$
, with a similar convention when working in the inner region polar coordinates
![]() $(\hat{R},\unicode[STIX]{x1D703})$
, or any other coordinate system in the paper.
$(\hat{R},\unicode[STIX]{x1D703})$
, or any other coordinate system in the paper.
3 Outer region as
 $t\rightarrow 0^{+}$
$t\rightarrow 0^{+}$
We begin in an outer region in which
![]() $(\overline{x},y)\in \overline{{\mathcal{D}}}(t)=O(1)$
as
$(\overline{x},y)\in \overline{{\mathcal{D}}}(t)=O(1)$
as
![]() $t\rightarrow 0^{+}$
, after which we require additional asymptotic regions to complete the structure, in which
$t\rightarrow 0^{+}$
, after which we require additional asymptotic regions to complete the structure, in which
![]() $(\overline{x},y)\in \overline{{\mathcal{D}}}(t)=o(1)$
as
$(\overline{x},y)\in \overline{{\mathcal{D}}}(t)=o(1)$
as
![]() $t\rightarrow 0^{+}$
. It is the structure in the innermost region that captures the initial dynamics of the interaction between the plate and fluid free surface. Conditions (2.6) and (2.8), together with (2.3), require that
$t\rightarrow 0^{+}$
. It is the structure in the innermost region that captures the initial dynamics of the interaction between the plate and fluid free surface. Conditions (2.6) and (2.8), together with (2.3), require that
![]() $\unicode[STIX]{x1D719}=O(t)$
and
$\unicode[STIX]{x1D719}=O(t)$
and
![]() $\unicode[STIX]{x1D702}=O(t^{2})$
as
$\unicode[STIX]{x1D702}=O(t^{2})$
as
![]() $t\rightarrow 0^{+}$
in the outer region. Thus, we introduce the asymptotic expansions
$t\rightarrow 0^{+}$
in the outer region. Thus, we introduce the asymptotic expansions
as
![]() $t\rightarrow 0^{+}$
in the outer region, with the factor
$t\rightarrow 0^{+}$
in the outer region, with the factor
![]() $\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC}$
in (3.1) included for algebraic convenience at a later stage. On substitution from (3.1) into [IBVP], we obtain the leading-order problem for
$\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC}$
in (3.1) included for algebraic convenience at a later stage. On substitution from (3.1) into [IBVP], we obtain the leading-order problem for
![]() $\overline{\unicode[STIX]{x1D719}}$
as
$\overline{\unicode[STIX]{x1D719}}$
as
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FB}^{2}\overline{\unicode[STIX]{x1D719}}=0,\quad (\overline{x},y)\in {\mathcal{D}}(0);\\ \unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\hat{\boldsymbol{n}}=1,\quad y=-\overline{x}\tan \unicode[STIX]{x1D6FC},\;0<\overline{x}<\cot \unicode[STIX]{x1D6FC};\\ \overline{\unicode[STIX]{x1D719}}_{y}=0,\quad y=-1,\;\overline{x}>\cot \unicode[STIX]{x1D6FC};\\ \overline{\unicode[STIX]{x1D719}}=0,\quad y=0,\;\overline{x}>0;\\ |\unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}|\rightarrow 0\quad \text{as}~\overline{x}\rightarrow \infty ,~\text{uniformly for}~-1\leqslant y\leqslant 0.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FB}^{2}\overline{\unicode[STIX]{x1D719}}=0,\quad (\overline{x},y)\in {\mathcal{D}}(0);\\ \unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}\boldsymbol{\cdot }\hat{\boldsymbol{n}}=1,\quad y=-\overline{x}\tan \unicode[STIX]{x1D6FC},\;0<\overline{x}<\cot \unicode[STIX]{x1D6FC};\\ \overline{\unicode[STIX]{x1D719}}_{y}=0,\quad y=-1,\;\overline{x}>\cot \unicode[STIX]{x1D6FC};\\ \overline{\unicode[STIX]{x1D719}}=0,\quad y=0,\;\overline{x}>0;\\ |\unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}|\rightarrow 0\quad \text{as}~\overline{x}\rightarrow \infty ,~\text{uniformly for}~-1\leqslant y\leqslant 0.\end{array}\right\}\end{eqnarray}$$
After this,
![]() $\overline{\unicode[STIX]{x1D702}}$
is given by
$\overline{\unicode[STIX]{x1D702}}$
is given by
Hence,
![]() $\overline{\unicode[STIX]{x1D719}}$
is the solution to the linear harmonic boundary value problem (3.2) above, defined on the fixed semi-infinite polygonal domain
$\overline{\unicode[STIX]{x1D719}}$
is the solution to the linear harmonic boundary value problem (3.2) above, defined on the fixed semi-infinite polygonal domain
![]() $\overline{{\mathcal{D}}}(0)$
, and, according to (2.16), we require
$\overline{{\mathcal{D}}}(0)$
, and, according to (2.16), we require
We remark that a problem similar to (3.1)–(3.4) arose in the case of
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
with impulsive initial motion in Wu (Reference Wu2001). Although the possibility of allowing
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/2$
with impulsive initial motion in Wu (Reference Wu2001). Although the possibility of allowing
![]() $|\unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}|$
to have an integrable singularity at
$|\unicode[STIX]{x1D735}\overline{\unicode[STIX]{x1D719}}|$
to have an integrable singularity at
![]() $(\overline{x},y)=(0,0)$
violates the full regularity conditions (2.16) on
$(\overline{x},y)=(0,0)$
violates the full regularity conditions (2.16) on
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D702}$
, via (3.1) and (3.3), it is necessary to ensure the existence of a solution to (3.2). The problem (3.2), which is independent of the dimensionless acceleration
$\unicode[STIX]{x1D702}$
, via (3.1) and (3.3), it is necessary to ensure the existence of a solution to (3.2). The problem (3.2), which is independent of the dimensionless acceleration
![]() $\unicode[STIX]{x1D70E}$
, was considered in detail in Needham et al. (Reference Needham, Chamberlain and Billingham2008), where it was established that there exist real constants
$\unicode[STIX]{x1D70E}$
, was considered in detail in Needham et al. (Reference Needham, Chamberlain and Billingham2008), where it was established that there exist real constants
![]() $A_{n}$
,
$A_{n}$
,
![]() $B_{n}$
and
$B_{n}$
and
![]() $C_{n}$
$C_{n}$
![]() $(n=0,1,2,\ldots )$
such that
$(n=0,1,2,\ldots )$
such that
for
![]() $0\leqslant r<\text{cosec}\,\unicode[STIX]{x1D6FC}$
,
$0\leqslant r<\text{cosec}\,\unicode[STIX]{x1D6FC}$
,
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, where
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, where
![]() $\overline{x}=r\cos \unicode[STIX]{x1D703}$
and
$\overline{x}=r\cos \unicode[STIX]{x1D703}$
and
![]() $y=r\sin \unicode[STIX]{x1D703}$
, while
$y=r\sin \unicode[STIX]{x1D703}$
, while
for
![]() $0\leqslant \unicode[STIX]{x1D70C}<1$
,
$0\leqslant \unicode[STIX]{x1D70C}<1$
,
![]() $0\leqslant \overline{\unicode[STIX]{x1D703}}\leqslant \unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC}$
, where
$0\leqslant \overline{\unicode[STIX]{x1D703}}\leqslant \unicode[STIX]{x03C0}-\unicode[STIX]{x1D6FC}$
, where
![]() $\overline{x}-\cot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}\cos \overline{\unicode[STIX]{x1D703}}$
and
$\overline{x}-\cot \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}\cos \overline{\unicode[STIX]{x1D703}}$
and
![]() $y+1=\unicode[STIX]{x1D70C}\sin \overline{\unicode[STIX]{x1D703}}$
, and
$y+1=\unicode[STIX]{x1D70C}\sin \overline{\unicode[STIX]{x1D703}}$
, and
for
![]() $\overline{x}>\cot \unicode[STIX]{x1D6FC}$
,
$\overline{x}>\cot \unicode[STIX]{x1D6FC}$
,
![]() $-1\leqslant y\leqslant 0$
. It then follows from (3.3), (3.5) and (3.7), that
$-1\leqslant y\leqslant 0$
. It then follows from (3.3), (3.5) and (3.7), that
for
![]() $0\leqslant \overline{x}<\text{cosec}\,\unicode[STIX]{x1D6FC}$
, and
$0\leqslant \overline{x}<\text{cosec}\,\unicode[STIX]{x1D6FC}$
, and
for
![]() $\overline{x}\geqslant \text{cosec}\,\unicode[STIX]{x1D6FC}$
. Here,
$\overline{x}\geqslant \text{cosec}\,\unicode[STIX]{x1D6FC}$
. Here,
![]() $k_{n}=(n+1/2)\unicode[STIX]{x03C0}$
,
$k_{n}=(n+1/2)\unicode[STIX]{x03C0}$
,
![]() $n=0,1,2,\ldots \,$
.
$n=0,1,2,\ldots \,$
.

Figure 4. The coefficient
![]() $A_{0}$
plotted against
$A_{0}$
plotted against
![]() $\unicode[STIX]{x1D6FC}$
. The solid line shows the analytical expression (3.10), while numerical approximations are shown as dots.
$\unicode[STIX]{x1D6FC}$
. The solid line shows the analytical expression (3.10), while numerical approximations are shown as dots.
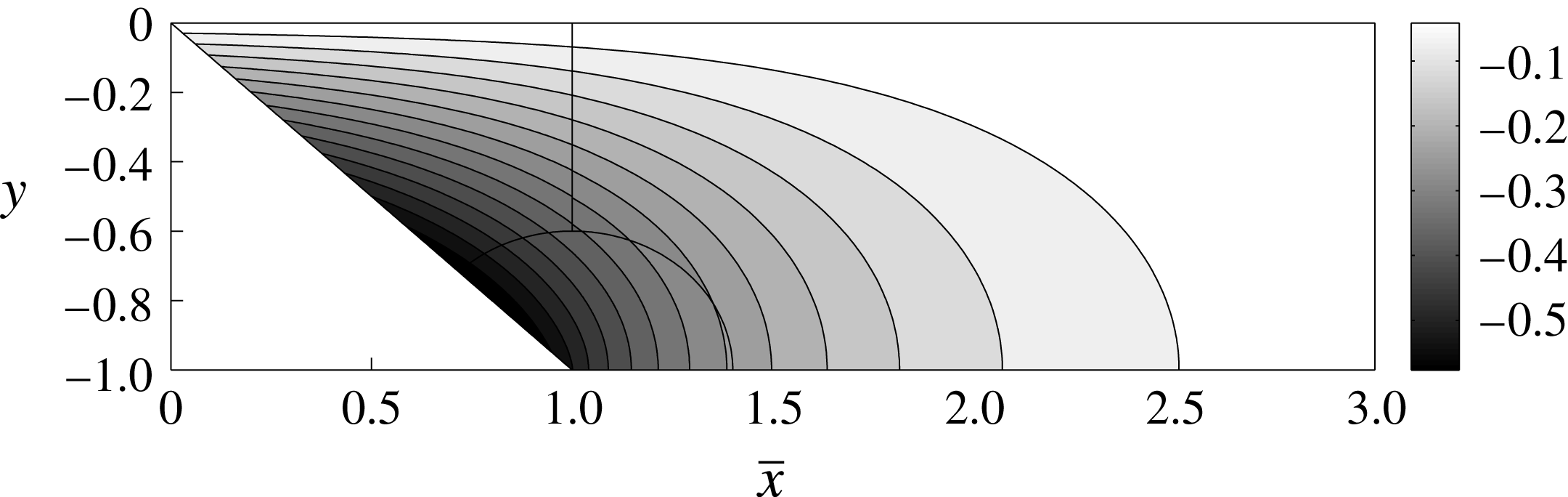
The three expressions (3.5), (3.6) and (3.7) are used to obtain numerical approximations to
![]() $\overline{\unicode[STIX]{x1D719}}$
and hence
$\overline{\unicode[STIX]{x1D719}}$
and hence
![]() $\overline{\unicode[STIX]{x1D702}}$
from (3.8) and (3.9). The approach used is to truncate each of the three infinite series and equate partial sums at collocation points in the intersection of domains of validity of (3.5), (3.6) and (3.7). The numerical procedure is completed by solving the resulting linear system of algebraic equations for the first
$\overline{\unicode[STIX]{x1D702}}$
from (3.8) and (3.9). The approach used is to truncate each of the three infinite series and equate partial sums at collocation points in the intersection of domains of validity of (3.5), (3.6) and (3.7). The numerical procedure is completed by solving the resulting linear system of algebraic equations for the first
![]() $N$
coefficients in each series. As in Needham et al. (Reference Needham, Chamberlain and Billingham2008), we choose
$N$
coefficients in each series. As in Needham et al. (Reference Needham, Chamberlain and Billingham2008), we choose
![]() $N=8$
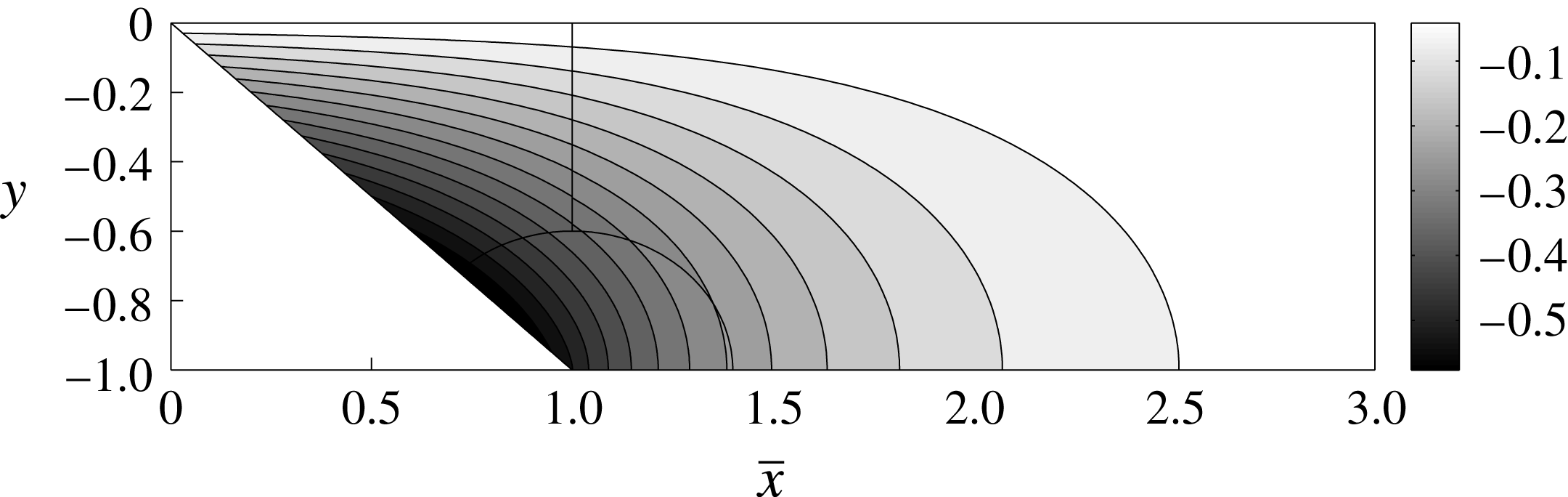
to achieve a sufficient level of convergence. We plot contours of
$N=8$
to achieve a sufficient level of convergence. We plot contours of
![]() $\overline{\unicode[STIX]{x1D719}}$
in figure 2, with lines separating regions where the numerical solution switches from the use of one of (3.5), (3.6) or (3.7) to another, noting that there is no visible distortion of the contours across these arcs. Having approximated
$\overline{\unicode[STIX]{x1D719}}$
in figure 2, with lines separating regions where the numerical solution switches from the use of one of (3.5), (3.6) or (3.7) to another, noting that there is no visible distortion of the contours across these arcs. Having approximated
![]() $\overline{\unicode[STIX]{x1D719}}$
, we then obtain
$\overline{\unicode[STIX]{x1D719}}$
, we then obtain
![]() $\overline{\unicode[STIX]{x1D702}}$
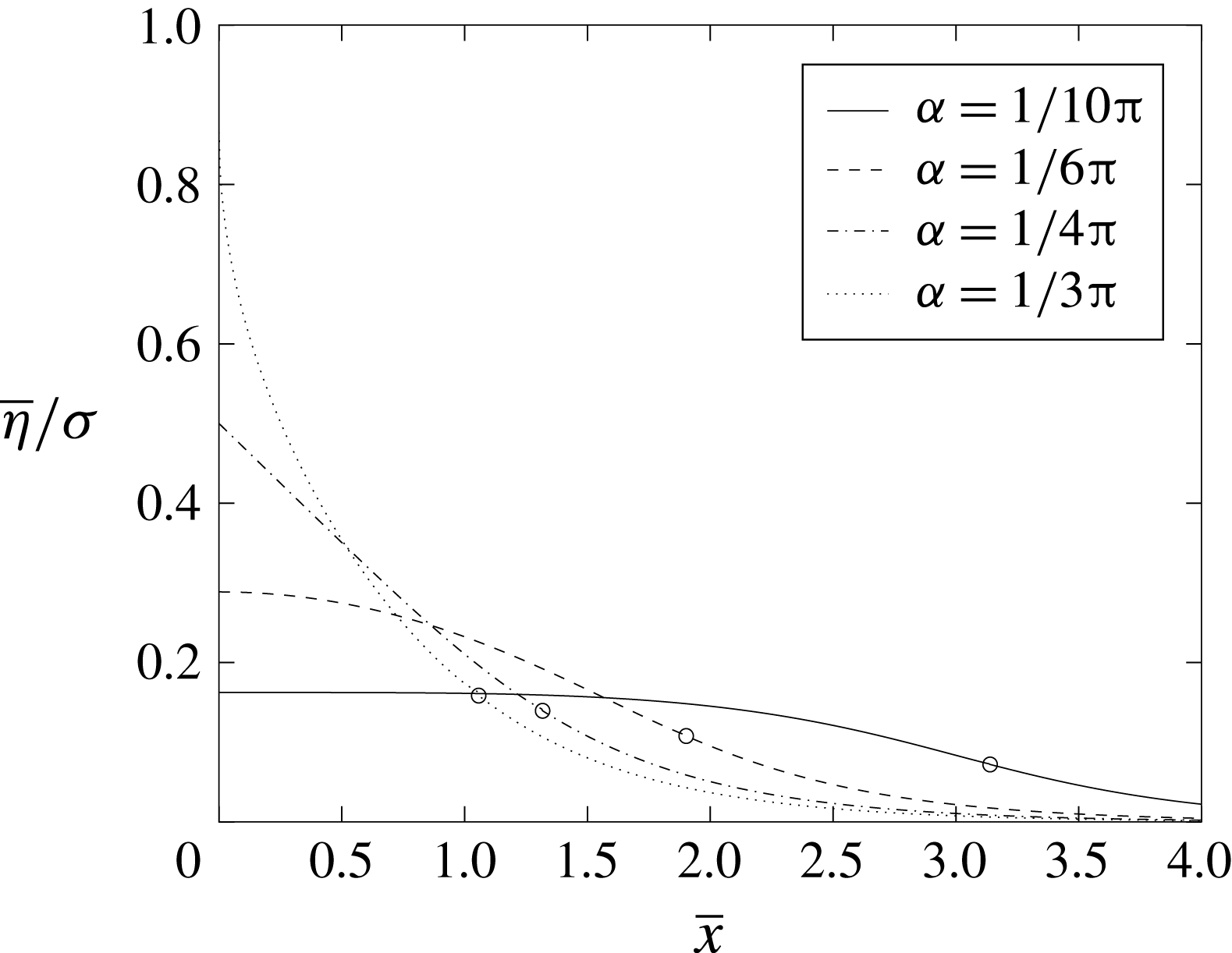
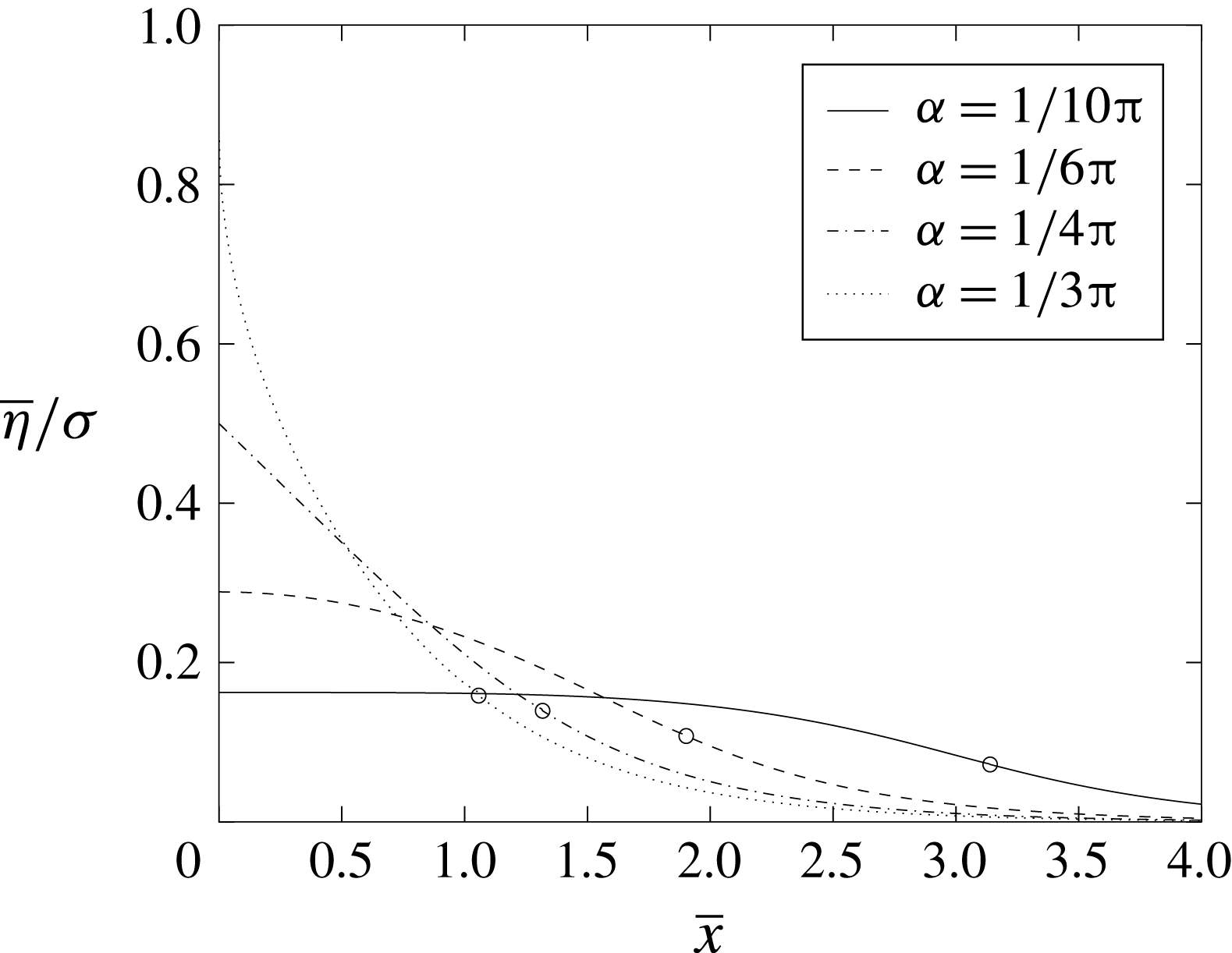
directly from (3.8) and (3.9). Figure 3 shows
$\overline{\unicode[STIX]{x1D702}}$
directly from (3.8) and (3.9). Figure 3 shows
![]() $\overline{\unicode[STIX]{x1D702}}$
, scaled with respect to
$\overline{\unicode[STIX]{x1D702}}$
, scaled with respect to
![]() $\unicode[STIX]{x1D70E}$
, for four values of
$\unicode[STIX]{x1D70E}$
, for four values of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
The coefficient
![]() $A_{0}$
in (3.5) and (3.8) (which depends solely upon
$A_{0}$
in (3.5) and (3.8) (which depends solely upon
![]() $\unicode[STIX]{x1D6FC}$
) will be of particular interest later, when we perform asymptotic matching of the outer and inner regions, and figure 4 shows
$\unicode[STIX]{x1D6FC}$
) will be of particular interest later, when we perform asymptotic matching of the outer and inner regions, and figure 4 shows
![]() $A_{0}$
plotted against
$A_{0}$
plotted against
![]() $\unicode[STIX]{x1D6FC}$
, along with the analytical expression
$\unicode[STIX]{x1D6FC}$
, along with the analytical expression
which is derived in Needham et al. (Reference Needham, Chamberlain and Billingham2008) and from which we obtain
The dynamic pressure in the outer region has the asymptotic expansion, from (2.15) and (3.1),
as
![]() $t\rightarrow 0^{+}$
, where
$t\rightarrow 0^{+}$
, where
Thus, the level curves of
![]() $\overline{\unicode[STIX]{x1D719}}$
plotted in figure 2 correspond, through (3.13), to the leading-order isobars of the dynamic pressure in the outer region. We see that, when
$\overline{\unicode[STIX]{x1D719}}$
plotted in figure 2 correspond, through (3.13), to the leading-order isobars of the dynamic pressure in the outer region. We see that, when
![]() $\unicode[STIX]{x1D70E}<0$
, there is a region of low pressure close to the base of the plate, and when
$\unicode[STIX]{x1D70E}<0$
, there is a region of low pressure close to the base of the plate, and when
![]() $\unicode[STIX]{x1D70E}>0$
, there is a region of high pressure close to the base of the plate. The effect this has on the free surface, close to the contact point with the plate, will be considered later.
$\unicode[STIX]{x1D70E}>0$
, there is a region of high pressure close to the base of the plate. The effect this has on the free surface, close to the contact point with the plate, will be considered later.
We see from (3.5), (3.6), (3.8) and (3.9) that the leading-order terms in the outer region asymptotic expansions (3.1) satisfy the regularity requirements (2.16), except in a neighbourhood of the initial location of the intersection point of the free surface and the plate, at
![]() $(\overline{x},y)=(0,0)\in \overline{{\mathcal{D}}}(0)$
. In particular, we have from (3.5) and (3.8) that
$(\overline{x},y)=(0,0)\in \overline{{\mathcal{D}}}(0)$
. In particular, we have from (3.5) and (3.8) that
as
![]() $r\rightarrow 0^{+}$
, when
$r\rightarrow 0^{+}$
, when
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, and
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, and
as
![]() $\overline{x}\rightarrow 0^{+}$
. It follows from (3.14) that
$\overline{x}\rightarrow 0^{+}$
. It follows from (3.14) that
as
![]() $r\rightarrow 0$
, when
$r\rightarrow 0$
, when
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Equation (3.15) reveals a weak singularity in
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. Equation (3.15) reveals a weak singularity in
![]() $\overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x})$
as
$\overline{\unicode[STIX]{x1D702}}^{\prime }(\overline{x})$
as
![]() $\overline{x}\rightarrow 0^{+}$
. Further investigation reveals that this singular behaviour is compounded in successively higher-order terms in the asymptotic expansions (3.1) in the outer region, and so the regularity conditions (2.16) fail to be satisfied by the outer region asymptotic expansions (3.1) in a neighbourhood of the initial contact point of the free surface and the plate, where
$\overline{x}\rightarrow 0^{+}$
. Further investigation reveals that this singular behaviour is compounded in successively higher-order terms in the asymptotic expansions (3.1) in the outer region, and so the regularity conditions (2.16) fail to be satisfied by the outer region asymptotic expansions (3.1) in a neighbourhood of the initial contact point of the free surface and the plate, where
![]() $(\overline{x},y)=o(1)$
as
$(\overline{x},y)=o(1)$
as
![]() $t\rightarrow 0^{+}$
. This requires the introduction of an inner region in order to capture the full regularity in the neighbourhood of the intersection point of the plate and the free surface.
$t\rightarrow 0^{+}$
. This requires the introduction of an inner region in order to capture the full regularity in the neighbourhood of the intersection point of the plate and the free surface.
4 Inner region as
 $t\rightarrow 0^{+}$
$t\rightarrow 0^{+}$
We now consider the inner region in the solution to [IBVP] as
![]() $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
4.1 Inner region structure
We have
![]() $(\overline{x},y)=O(\unicode[STIX]{x1D6FF}(t))$
, with
$(\overline{x},y)=O(\unicode[STIX]{x1D6FF}(t))$
, with
![]() $\unicode[STIX]{x1D6FF}(t)=o(1)$
as
$\unicode[STIX]{x1D6FF}(t)=o(1)$
as
![]() $t\rightarrow 0^{+}$
, in the inner region. It then follows from (3.1) and (3.15) that
$t\rightarrow 0^{+}$
, in the inner region. It then follows from (3.1) and (3.15) that
![]() $\unicode[STIX]{x1D702}=O(t^{2})$
as
$\unicode[STIX]{x1D702}=O(t^{2})$
as
![]() $t\rightarrow 0^{+}$
in the inner region, so that, to capture the free surface in the inner region, we must take
$t\rightarrow 0^{+}$
in the inner region, so that, to capture the free surface in the inner region, we must take
![]() $\unicode[STIX]{x1D6FF}(t)=O(t^{2})$
; therefore, without loss of generality, we set
$\unicode[STIX]{x1D6FF}(t)=O(t^{2})$
; therefore, without loss of generality, we set
![]() $\unicode[STIX]{x1D6FF}(t)=t^{2}$
. An examination of (3.1) and (3.14) then requires that
$\unicode[STIX]{x1D6FF}(t)=t^{2}$
. An examination of (3.1) and (3.14) then requires that
![]() $\unicode[STIX]{x1D719}=O(t^{3})$
as
$\unicode[STIX]{x1D719}=O(t^{3})$
as
![]() $t\rightarrow 0^{+}$
in the inner region, while (3.12) and (3.13) require that
$t\rightarrow 0^{+}$
in the inner region, while (3.12) and (3.13) require that
![]() $p_{d}=O(t^{2})$
as
$p_{d}=O(t^{2})$
as
![]() $t\rightarrow 0^{+}$
in the inner region. Thus, we introduce the scaled inner region coordinates
$t\rightarrow 0^{+}$
in the inner region. Thus, we introduce the scaled inner region coordinates
![]() $(X,Y)$
by the transformation
$(X,Y)$
by the transformation
where
![]() $(X,Y)=O(1)$
as
$(X,Y)=O(1)$
as
![]() $t\rightarrow 0^{+}$
in the inner region. The location of the plate in the inner region is given by
$t\rightarrow 0^{+}$
in the inner region. The location of the plate in the inner region is given by
![]() $Y=-X\tan \unicode[STIX]{x1D6FC}$
, and the contact point is denoted by
$Y=-X\tan \unicode[STIX]{x1D6FC}$
, and the contact point is denoted by
![]() $(X,Y)=(X_{p}(t),Y_{p}(t))$
, with
$(X,Y)=(X_{p}(t),Y_{p}(t))$
, with
![]() $\overline{x}_{p}(t)=t^{2}X_{p}(t)$
and
$\overline{x}_{p}(t)=t^{2}X_{p}(t)$
and
![]() $y_{p}(t)=t^{2}Y_{p}(t)$
.
$y_{p}(t)=t^{2}Y_{p}(t)$
.
We now write the free surface and velocity potential in the inner region as
where
![]() $\unicode[STIX]{x1D702}_{I}(X,t)$
,
$\unicode[STIX]{x1D702}_{I}(X,t)$
,
![]() $\unicode[STIX]{x1D719}_{I}(X,Y,t)=O(1)$
as
$\unicode[STIX]{x1D719}_{I}(X,Y,t)=O(1)$
as
![]() $t\rightarrow 0^{+}$
, after which we introduce the inner region asymptotic expansions as
$t\rightarrow 0^{+}$
, after which we introduce the inner region asymptotic expansions as
as
![]() $t\rightarrow 0^{+}$
in the inner region, where the form of the correction terms has been deduced from (4.1), together with (3.1), (3.5) and (3.8). It then follows from (4.1) and (4.2) that the free surface in the inner region is located at
$t\rightarrow 0^{+}$
in the inner region, where the form of the correction terms has been deduced from (4.1), together with (3.1), (3.5) and (3.8). It then follows from (4.1) and (4.2) that the free surface in the inner region is located at
and hence we must expand
as
![]() $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
We now write [IBVP] in terms of the inner coordinates and variables, and substitute from (4.3). The leading-order problem, when supplemented with matching conditions to the outer region (obtained through the use of Van Dyke’s matching principle (Van Dyke Reference Van Dyke1964)), has the solution (see Gallagher Reference Gallagher2015)
where
It then follows from (4.6) and (4.7), on using (4.1)–(4.3), that the regularity conditions (2.16) are satisfied at leading order in the inner region. We now formulate the problem at
![]() $O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
, where it is convenient to introduce coordinates
$O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
, where it is convenient to introduce coordinates
![]() $(\overline{X},\overline{Y})$
according to
$(\overline{X},\overline{Y})$
according to
which is simply a shift of origin from the original inner coordinates
![]() $(X,Y)$
. We then write
$(X,Y)$
. We then write
with the
![]() $A_{0}\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC}$
scaling chosen for algebraic convenience. We now obtain the problem for
$A_{0}\unicode[STIX]{x1D70E}\sin \unicode[STIX]{x1D6FC}$
scaling chosen for algebraic convenience. We now obtain the problem for
![]() $\widehat{\unicode[STIX]{x1D719}}$
,
$\widehat{\unicode[STIX]{x1D719}}$
,
![]() $\widehat{\unicode[STIX]{x1D702}}$
and
$\widehat{\unicode[STIX]{x1D702}}$
and
![]() $X_{1}$
as
$X_{1}$
as
Here,
![]() $\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
, the final conditions (4.15) and (4.16) are the matching conditions with the outer region, and we have introduced polar coordinates
$\overline{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\overline{Y})$
, the final conditions (4.15) and (4.16) are the matching conditions with the outer region, and we have introduced polar coordinates
![]() $(\overline{R},\unicode[STIX]{x1D703})$
, given by
$(\overline{R},\unicode[STIX]{x1D703})$
, given by
![]() $\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
$\overline{X}=\overline{R}\cos \unicode[STIX]{x1D703}$
,
![]() $\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
. After this, we have
$\overline{Y}=\overline{R}\sin \unicode[STIX]{x1D703}$
. After this, we have
We now notice that in the boundary value problem (4.11)–(4.17) (which is the same as that derived in Needham et al. (Reference Needham, Chamberlain and Billingham2008), where this observation was overlooked), the dimensionless acceleration
![]() $\unicode[STIX]{x1D70E}$
appears only in the dynamic boundary condition (4.14) as
$\unicode[STIX]{x1D70E}$
appears only in the dynamic boundary condition (4.14) as
![]() $(1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC})$
. Thus, we set
$(1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC})$
. Thus, we set
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
and, in the case that
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
and, in the case that
![]() $\unicode[STIX]{x1D707}\neq 0$
, we introduce the following scalings:
$\unicode[STIX]{x1D707}\neq 0$
, we introduce the following scalings:
The corresponding boundary value problem for
![]() $\unicode[STIX]{x1D6F7}(\widehat{X},\widehat{Y})$
and
$\unicode[STIX]{x1D6F7}(\widehat{X},\widehat{Y})$
and
![]() $H(\widehat{X})$
is now independent of
$H(\widehat{X})$
is now independent of
![]() $\unicode[STIX]{x1D707}$
, and is reducible to a scalar linear harmonic problem in
$\unicode[STIX]{x1D707}$
, and is reducible to a scalar linear harmonic problem in
![]() $\unicode[STIX]{x1D6F7}$
, allowing us to write, explicitly,
$\unicode[STIX]{x1D6F7}$
, allowing us to write, explicitly,
with
![]() $+$
and
$+$
and
![]() $-$
corresponding to
$-$
corresponding to
![]() $\unicode[STIX]{x1D707}>0$
and
$\unicode[STIX]{x1D707}>0$
and
![]() $\unicode[STIX]{x1D707}<0$
respectively,
$\unicode[STIX]{x1D707}<0$
respectively,
and
after which we obtain the two linear harmonic boundary value problems for
![]() $\unicode[STIX]{x1D6F7}$
alone (depending upon whether
$\unicode[STIX]{x1D6F7}$
alone (depending upon whether
![]() $\unicode[STIX]{x1D707}>0$
or
$\unicode[STIX]{x1D707}>0$
or
![]() $\unicode[STIX]{x1D707}<0$
), hereafter termed
$\unicode[STIX]{x1D707}<0$
), hereafter termed
![]() $\text{(PBVP)}^{\pm }$
, given by
$\text{(PBVP)}^{\pm }$
, given by
Here
![]() $\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{Y})$
,
$\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{X},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{Y})$
,
![]() $(\widehat{R},\unicode[STIX]{x1D703})$
are polar coordinates given by
$(\widehat{R},\unicode[STIX]{x1D703})$
are polar coordinates given by
![]() $\widehat{X}=\widehat{R}\cos \unicode[STIX]{x1D703}$
and
$\widehat{X}=\widehat{R}\cos \unicode[STIX]{x1D703}$
and
![]() $\widehat{Y}=\widehat{R}\sin \unicode[STIX]{x1D703}$
, and the
$\widehat{Y}=\widehat{R}\sin \unicode[STIX]{x1D703}$
, and the
![]() $+/-$
sign in
$+/-$
sign in
![]() $\text{(PBVP)}^{\pm }$
corresponds to the cases
$\text{(PBVP)}^{\pm }$
corresponds to the cases
![]() $\unicode[STIX]{x1D707}>0$
and
$\unicode[STIX]{x1D707}>0$
and
![]() $\unicode[STIX]{x1D707}<0$
respectively.
$\unicode[STIX]{x1D707}<0$
respectively.
4.2 Analysis of the boundary value problem (4.11)–(4.17)
The full regularity conditions (2.16) on [IBVP] require regularity conditions on each of
![]() $\text{(PBVP)}^{\pm }$
(and then on
$\text{(PBVP)}^{\pm }$
(and then on
![]() $H$
through (4.19)), namely
$H$
through (4.19)), namely
where
![]() ${\mathcal{T}}=\{(\widehat{R},\unicode[STIX]{x1D703}):\widehat{R}>0,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0\}$
. It is worth observing here that for fixed
${\mathcal{T}}=\{(\widehat{R},\unicode[STIX]{x1D703}):\widehat{R}>0,-\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D703}<0\}$
. It is worth observing here that for fixed
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, the scaling (4.10) reflects a change of sign as
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, the scaling (4.10) reflects a change of sign as
![]() $\unicode[STIX]{x1D70E}$
changes sign. However, the scaling (4.18) indicates a change in structure as
$\unicode[STIX]{x1D70E}$
changes sign. However, the scaling (4.18) indicates a change in structure as
![]() $\unicode[STIX]{x1D707}$
changes sign and the dimensionless acceleration of the plate in withdrawal has
$\unicode[STIX]{x1D707}$
changes sign and the dimensionless acceleration of the plate in withdrawal has
![]() $\unicode[STIX]{x1D70E}<-(\tan \unicode[STIX]{x1D6FC})^{-1}$
.
$\unicode[STIX]{x1D70E}<-(\tan \unicode[STIX]{x1D6FC})^{-1}$
.
We begin by examining whether
![]() $\text{(PBVP)}^{\pm }$
will admit a solution local to the tip of the wedge, as
$\text{(PBVP)}^{\pm }$
will admit a solution local to the tip of the wedge, as
![]() $\widehat{R}\rightarrow 0$
,
$\widehat{R}\rightarrow 0$
,
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, which has the regularity required by (4.26). It is readily established that any solution to
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, which has the regularity required by (4.26). It is readily established that any solution to
![]() $\text{(PBVP)}^{\pm }$
must have
$\text{(PBVP)}^{\pm }$
must have
as
![]() $\widehat{R}\rightarrow 0$
, uniformly for
$\widehat{R}\rightarrow 0$
, uniformly for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, and some globally determined real constants (which will depend upon
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, and some globally determined real constants (which will depend upon
![]() $\unicode[STIX]{x1D6FC}$
)
$\unicode[STIX]{x1D6FC}$
)
![]() $a_{0}$
,
$a_{0}$
,
![]() $b_{n}$
(
$b_{n}$
(
![]() $n=1,2,\ldots$
) not all zero, with
$n=1,2,\ldots$
) not all zero, with
![]() $\unicode[STIX]{x1D6F7}_{0}^{0}$
,
$\unicode[STIX]{x1D6F7}_{0}^{0}$
,
![]() $\unicode[STIX]{x1D6F7}_{n}\rightarrow 1$
(
$\unicode[STIX]{x1D6F7}_{n}\rightarrow 1$
(
![]() $n=1,2,\ldots$
) as
$n=1,2,\ldots$
) as
![]() $\widehat{R}\rightarrow 0$
, uniformly for
$\widehat{R}\rightarrow 0$
, uniformly for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. On substitution from (4.27) into
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. On substitution from (4.27) into
![]() $\text{(PBVP)}^{\pm }$
, we obtain
$\text{(PBVP)}^{\pm }$
, we obtain
as
![]() $\widehat{R}\rightarrow 0$
, for
$\widehat{R}\rightarrow 0$
, for
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. We then have, from (4.19) and (4.28),
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
. We then have, from (4.19) and (4.28),
 $$\begin{eqnarray}\displaystyle H(\widehat{X}) & {\sim} & \displaystyle \pm a_{0}\left[-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{0}^{0}(\widehat{X},0)+2\widehat{X}\unicode[STIX]{x1D6F7}_{0,\widehat{X}}^{0}(\widehat{X},0)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }b_{n}(-1)^{n}\left\{\left[(2n-1)\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}-1\right]\unicode[STIX]{x1D6F7}_{n}(\widehat{X},0)\widehat{X}^{n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\widehat{X}^{n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}\unicode[STIX]{x1D6F7}_{n,\widehat{X}}(\widehat{X},0)\vphantom{\left[\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right]}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H(\widehat{X}) & {\sim} & \displaystyle \pm a_{0}\left[-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{0}^{0}(\widehat{X},0)+2\widehat{X}\unicode[STIX]{x1D6F7}_{0,\widehat{X}}^{0}(\widehat{X},0)\right]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n=1}^{\infty }b_{n}(-1)^{n}\left\{\left[(2n-1)\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}-1\right]\unicode[STIX]{x1D6F7}_{n}(\widehat{X},0)\widehat{X}^{n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\widehat{X}^{n\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}\unicode[STIX]{x1D6F7}_{n,\widehat{X}}(\widehat{X},0)\vphantom{\left[\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right]}\right\},\end{eqnarray}$$
as
![]() $\widehat{X}\rightarrow 0$
. Thus, both of
$\widehat{X}\rightarrow 0$
. Thus, both of
![]() $\text{(PBVP)}^{\pm }$
will admit a solution with regularity (4.26) as
$\text{(PBVP)}^{\pm }$
will admit a solution with regularity (4.26) as
![]() $\widehat{X}$
,
$\widehat{X}$
,
![]() $\widehat{R}\rightarrow 0$
. Following Needham et al. (Reference Needham, Chamberlain and Billingham2008), we observe that both
$\widehat{R}\rightarrow 0$
. Following Needham et al. (Reference Needham, Chamberlain and Billingham2008), we observe that both
![]() $\text{(PBVP)}^{\pm }$
admit exact solution for the angles
$\text{(PBVP)}^{\pm }$
admit exact solution for the angles
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}\in (0,\unicode[STIX]{x03C0}/4]$
, where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}\in (0,\unicode[STIX]{x03C0}/4]$
, where
For
![]() $\text{(PBVP)}^{\pm }$
, we have the exact solution at
$\text{(PBVP)}^{\pm }$
, we have the exact solution at
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
![]() $(n=1,2,\ldots )$
given by
$(n=1,2,\ldots )$
given by
with, from (4.19),
where
![]() $\overline{a}_{n+1}=-1$
and
$\overline{a}_{n+1}=-1$
and
 $$\begin{eqnarray}\overline{a}_{p}=\frac{\displaystyle -(1/2)!(n+1)!\mathop{\prod }_{k=p+1}^{n+1}\sin (k\unicode[STIX]{x1D6FC}_{n})}{\displaystyle 4^{n+1-p}p!(n+1-p)!(n+3/2-p)!\mathop{\prod }_{k=p}^{n}\cos (k\unicode[STIX]{x1D6FC}_{n})},\quad p=0,1,2,\ldots ,n.\end{eqnarray}$$
$$\begin{eqnarray}\overline{a}_{p}=\frac{\displaystyle -(1/2)!(n+1)!\mathop{\prod }_{k=p+1}^{n+1}\sin (k\unicode[STIX]{x1D6FC}_{n})}{\displaystyle 4^{n+1-p}p!(n+1-p)!(n+3/2-p)!\mathop{\prod }_{k=p}^{n}\cos (k\unicode[STIX]{x1D6FC}_{n})},\quad p=0,1,2,\ldots ,n.\end{eqnarray}$$
Thus, when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
, from (4.31)–(4.33), we obtain the near-field constant
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
, from (4.31)–(4.33), we obtain the near-field constant
![]() $a_{0}$
in (4.27) as
$a_{0}$
in (4.27) as
 $$\begin{eqnarray}a_{0}=\frac{-(\pm 1)^{n+1}(1/2)!\displaystyle \mathop{\prod }_{k=1}^{n+1}\sin (k\unicode[STIX]{x1D6FC}_{n})}{4^{n+1}(n+3/2)!\displaystyle \mathop{\prod }_{k=0}^{n}\cos (k\unicode[STIX]{x1D6FC}_{n})},\end{eqnarray}$$
$$\begin{eqnarray}a_{0}=\frac{-(\pm 1)^{n+1}(1/2)!\displaystyle \mathop{\prod }_{k=1}^{n+1}\sin (k\unicode[STIX]{x1D6FC}_{n})}{4^{n+1}(n+3/2)!\displaystyle \mathop{\prod }_{k=0}^{n}\cos (k\unicode[STIX]{x1D6FC}_{n})},\end{eqnarray}$$
for
![]() $\text{(PBVP)}^{\pm }$
respectively. The simplest case occurs when
$\text{(PBVP)}^{\pm }$
respectively. The simplest case occurs when
![]() $n=1$
and
$n=1$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x03C0}/4$
, when, from (4.31)–(4.34), for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x03C0}/4$
, when, from (4.31)–(4.34), for
![]() $\text{(PBVP)}^{\pm }$
respectively,
$\text{(PBVP)}^{\pm }$
respectively,
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \!\unicode[STIX]{x1D6F7}(\widehat{R},\unicode[STIX]{x1D703})=-\frac{1}{60}-\!\left(\!\pm \frac{\sqrt{2}}{3}\right)\!\widehat{R}\cos \left(\!\unicode[STIX]{x1D703}+\frac{\unicode[STIX]{x03C0}}{4}\right)-\widehat{R}^{2}\cos 2\left(\!\unicode[STIX]{x1D703}+\frac{\unicode[STIX]{x03C0}}{4}\right),\quad \widehat{R}\geqslant 0,\;-\frac{\unicode[STIX]{x03C0}}{4}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\\ \!H(\widehat{X})=\pm {\textstyle \frac{1}{12}}+\widehat{X},\quad \widehat{X}\geqslant 0.\end{array}\!\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \!\unicode[STIX]{x1D6F7}(\widehat{R},\unicode[STIX]{x1D703})=-\frac{1}{60}-\!\left(\!\pm \frac{\sqrt{2}}{3}\right)\!\widehat{R}\cos \left(\!\unicode[STIX]{x1D703}+\frac{\unicode[STIX]{x03C0}}{4}\right)-\widehat{R}^{2}\cos 2\left(\!\unicode[STIX]{x1D703}+\frac{\unicode[STIX]{x03C0}}{4}\right),\quad \widehat{R}\geqslant 0,\;-\frac{\unicode[STIX]{x03C0}}{4}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\\ \!H(\widehat{X})=\pm {\textstyle \frac{1}{12}}+\widehat{X},\quad \widehat{X}\geqslant 0.\end{array}\!\right\}\end{eqnarray}$$
For the remaining values of
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, we must obtain a numerical solution of the two linear harmonic problems
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, we must obtain a numerical solution of the two linear harmonic problems
![]() $\text{(PBVP)}^{\pm }$
. Here, we use a finite difference method in terms of polar coordinates to discretise the wedge domain. The singularity of the coordinate system at the tip of the wedge (
$\text{(PBVP)}^{\pm }$
. Here, we use a finite difference method in terms of polar coordinates to discretise the wedge domain. The singularity of the coordinate system at the tip of the wedge (
![]() $\widehat{R}=0$
) requires that the regularity (4.26) is enforced as
$\widehat{R}=0$
) requires that the regularity (4.26) is enforced as
![]() $\widehat{R}\rightarrow 0$
, through the introduction of a near-field boundary condition given, from the near-field asymptotic form (4.27) and (4.28), as
$\widehat{R}\rightarrow 0$
, through the introduction of a near-field boundary condition given, from the near-field asymptotic form (4.27) and (4.28), as
with
![]() $\unicode[STIX]{x1D716}>0$
chosen to be sufficiently small. The near-field constant
$\unicode[STIX]{x1D716}>0$
chosen to be sufficiently small. The near-field constant
![]() $a_{0}$
in (4.27) is then approximated numerically for both of
$a_{0}$
in (4.27) is then approximated numerically for both of
![]() $\text{(PBVP)}^{\pm }$
. We now examine the results obtained from the numerical solution of
$\text{(PBVP)}^{\pm }$
. We now examine the results obtained from the numerical solution of
![]() $\text{(PBVP)}^{\pm }$
in turn.
$\text{(PBVP)}^{\pm }$
in turn.
4.3 Numerical results for
 $(PBVP)^{+}$
$(PBVP)^{+}$
We examine the results obtained from the numerical solution of
![]() $(\text{PBVP})^{+}$
. Figure 5 presents plots of the level curves of
$(\text{PBVP})^{+}$
. Figure 5 presents plots of the level curves of
![]() $\unicode[STIX]{x1D6F7}$
for
$\unicode[STIX]{x1D6F7}$
for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, computed using finite differences. Values of
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, computed using finite differences. Values of
![]() $\widehat{R}=2.5$
and
$\widehat{R}=2.5$
and
![]() $\unicode[STIX]{x1D716}=10^{-3}$
were found to be suitable for implementation of the boundary conditions (4.25) and (4.36). The cases
$\unicode[STIX]{x1D716}=10^{-3}$
were found to be suitable for implementation of the boundary conditions (4.25) and (4.36). The cases
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
permit exact solutions for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
permit exact solutions for
![]() $\unicode[STIX]{x1D6F7}$
as given in (4.31), and we plot these in figure 6. Comparisons show excellent agreement between these exact solutions and the numerical solutions at least up to the scales shown on the representative graphs. Figure 7 shows
$\unicode[STIX]{x1D6F7}$
as given in (4.31), and we plot these in figure 6. Comparisons show excellent agreement between these exact solutions and the numerical solutions at least up to the scales shown on the representative graphs. Figure 7 shows
![]() $H$
plotted against
$H$
plotted against
![]() $\widehat{X}$
for a number of angles
$\widehat{X}$
for a number of angles
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, and shows that the inner region has regularised the free surface elevation since
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, and shows that the inner region has regularised the free surface elevation since
![]() $H$
and its first derivative are bounded up to the plate.
$H$
and its first derivative are bounded up to the plate.
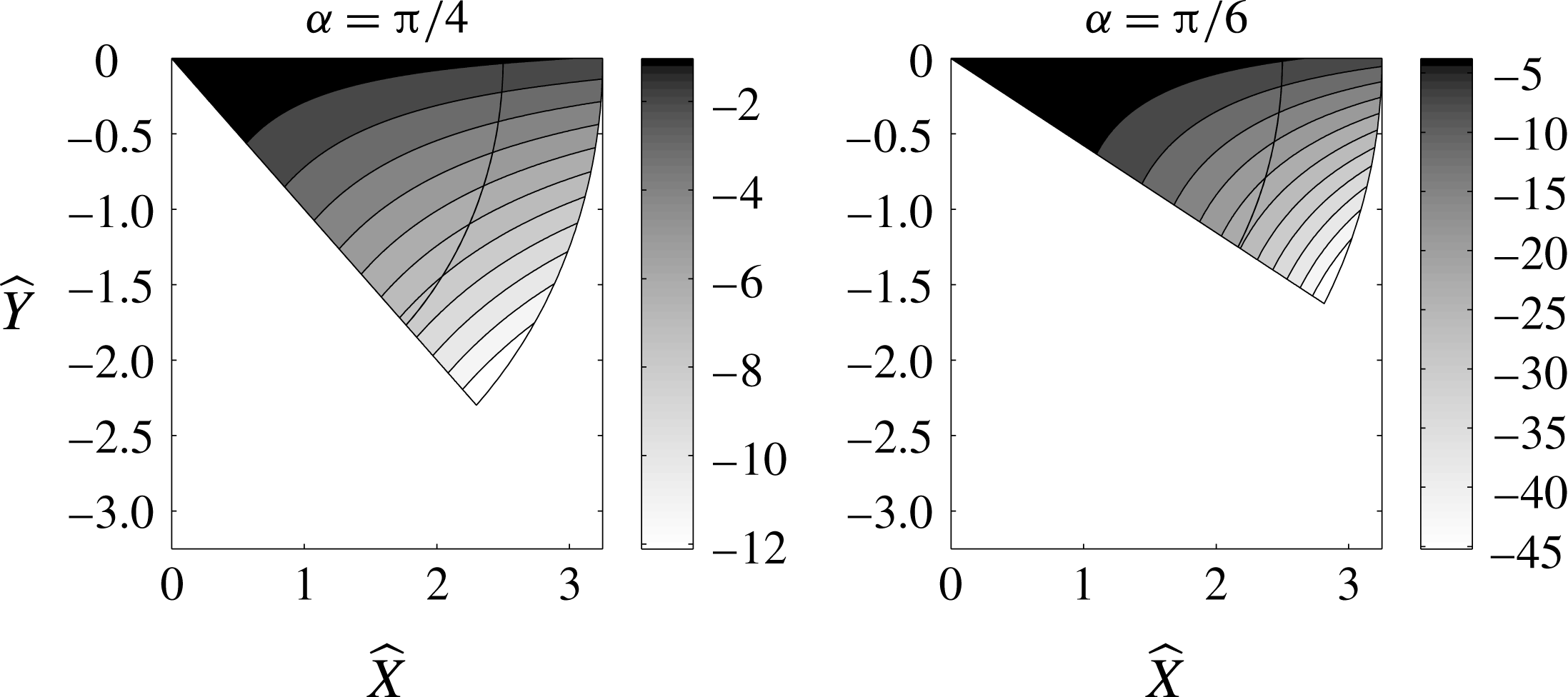
Figure 5. Contours of
![]() $\unicode[STIX]{x1D6F7}$
for the numerical solution of
$\unicode[STIX]{x1D6F7}$
for the numerical solution of
![]() $\text{(PBVP)}^{+}$
when
$\text{(PBVP)}^{+}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a black line shows
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a black line shows
![]() $\widehat{R}=2.5$
, after which the far-field asymptotic form (4.25) is plotted.
$\widehat{R}=2.5$
, after which the far-field asymptotic form (4.25) is plotted.
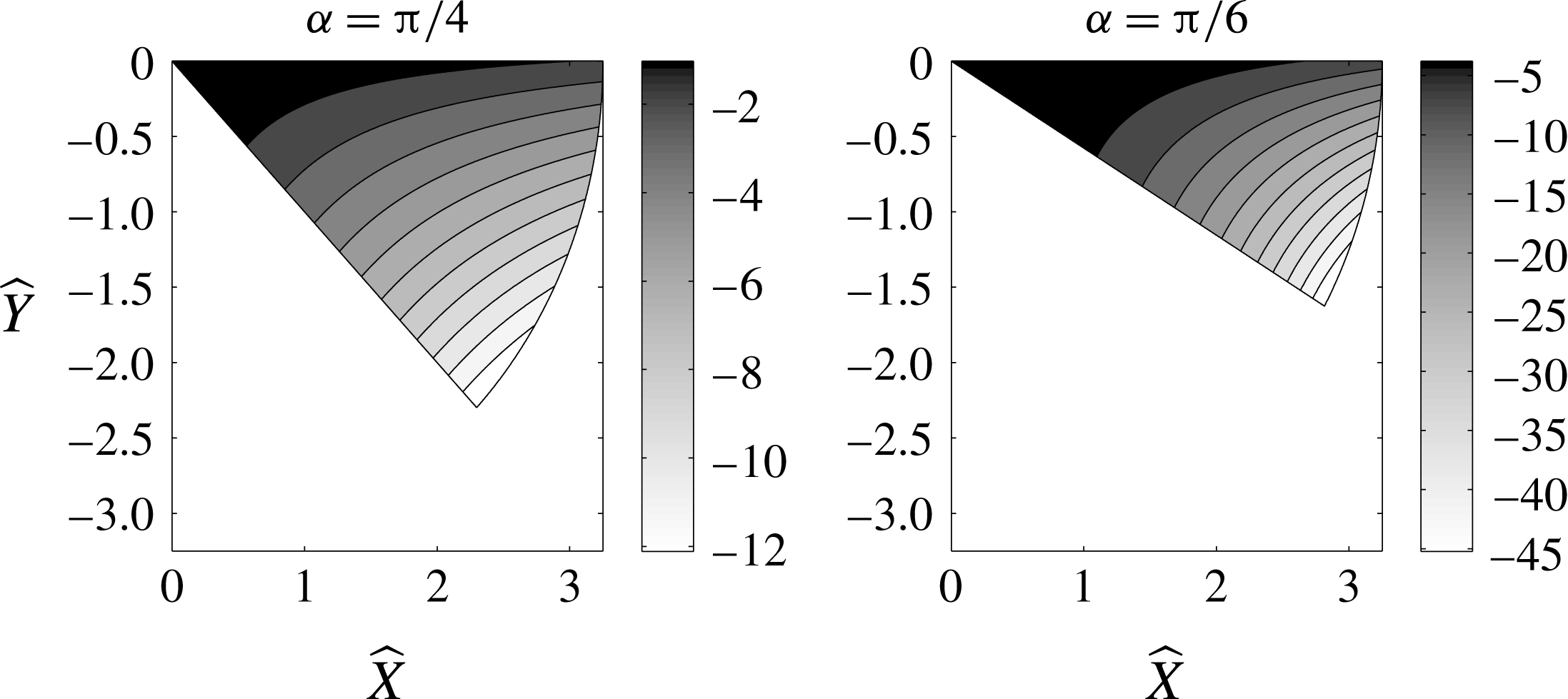
Figure 6. Contours of
![]() $\unicode[STIX]{x1D6F7}$
for the exact solution (4.31) of
$\unicode[STIX]{x1D6F7}$
for the exact solution (4.31) of
![]() $\text{(PBVP)}^{+}$
when
$\text{(PBVP)}^{+}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
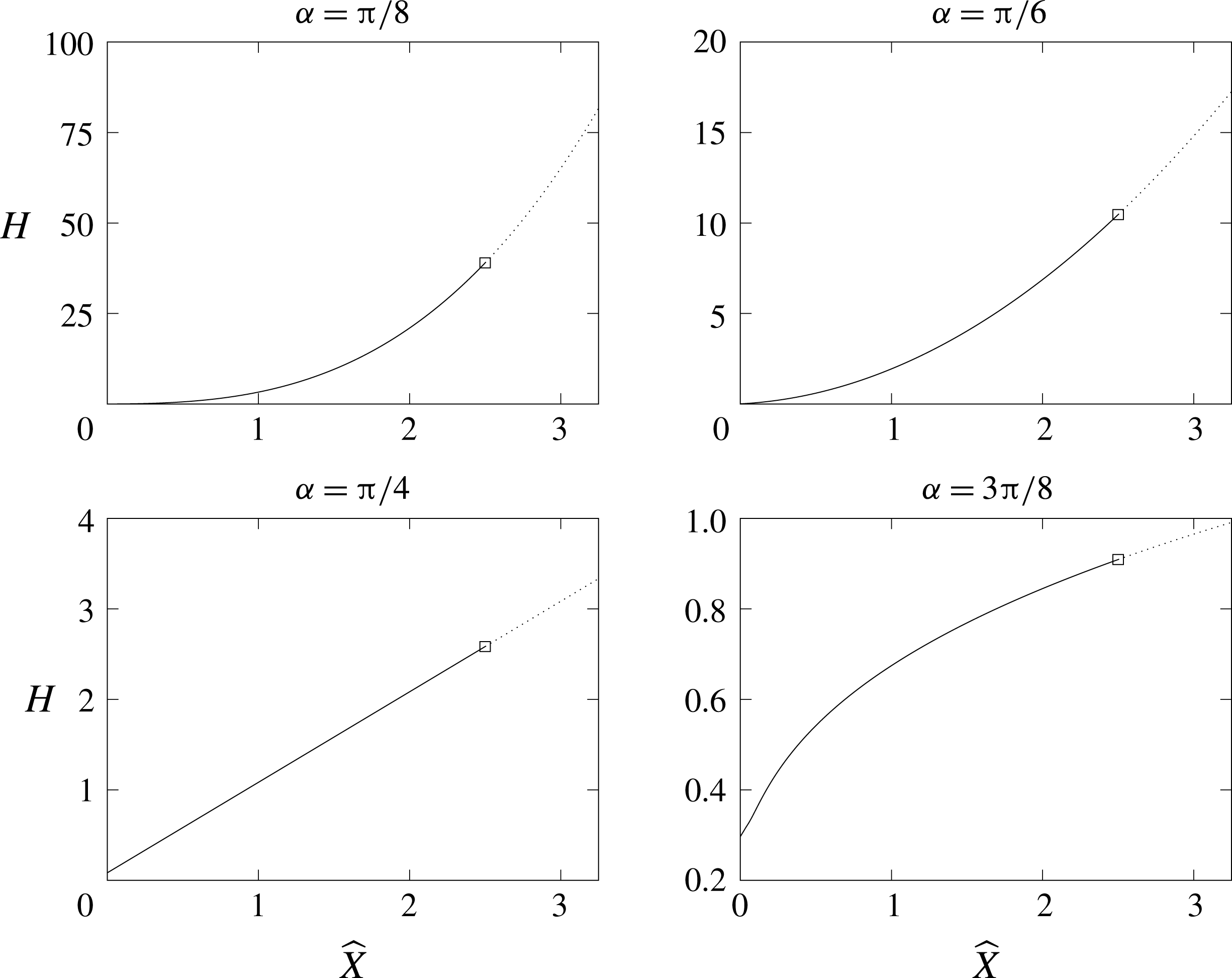
Figure 7. Graphs of
![]() $H$
for the numerical solution of
$H$
for the numerical solution of
![]() $(\text{PBVP})^{+}$
for a selection of angles
$(\text{PBVP})^{+}$
for a selection of angles
![]() $\unicode[STIX]{x1D6FC}$
. In each graph, a square shows
$\unicode[STIX]{x1D6FC}$
. In each graph, a square shows
![]() $\widehat{R}=2.5$
, after which the far-field asymptotic form (4.20) is plotted.
$\widehat{R}=2.5$
, after which the far-field asymptotic form (4.20) is plotted.
In figure 8, we show plots of
![]() $H(0)$
and
$H(0)$
and
![]() $H_{\widehat{X}}(0)$
against
$H_{\widehat{X}}(0)$
against
![]() $\unicode[STIX]{x1D6FC}$
. We see that as
$\unicode[STIX]{x1D6FC}$
. We see that as
![]() $\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
,
$\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
,
![]() $H(0)\rightarrow 0^{+}$
and
$H(0)\rightarrow 0^{+}$
and
![]() $H_{\widehat{X}}(0)\rightarrow 0^{+}$
, while as
$H_{\widehat{X}}(0)\rightarrow 0^{+}$
, while as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
,
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
,
![]() $H(0)\rightarrow 1/2$
and
$H(0)\rightarrow 1/2$
and
![]() $H_{\widehat{X}}(0)\rightarrow 0^{+}$
. We notice that
$H_{\widehat{X}}(0)\rightarrow 0^{+}$
. We notice that
![]() $H_{\widehat{X}}(0)$
has a maximum value close to
$H_{\widehat{X}}(0)$
has a maximum value close to
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
. As before, the angles that have exact solutions are shown as circles.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
. As before, the angles that have exact solutions are shown as circles.
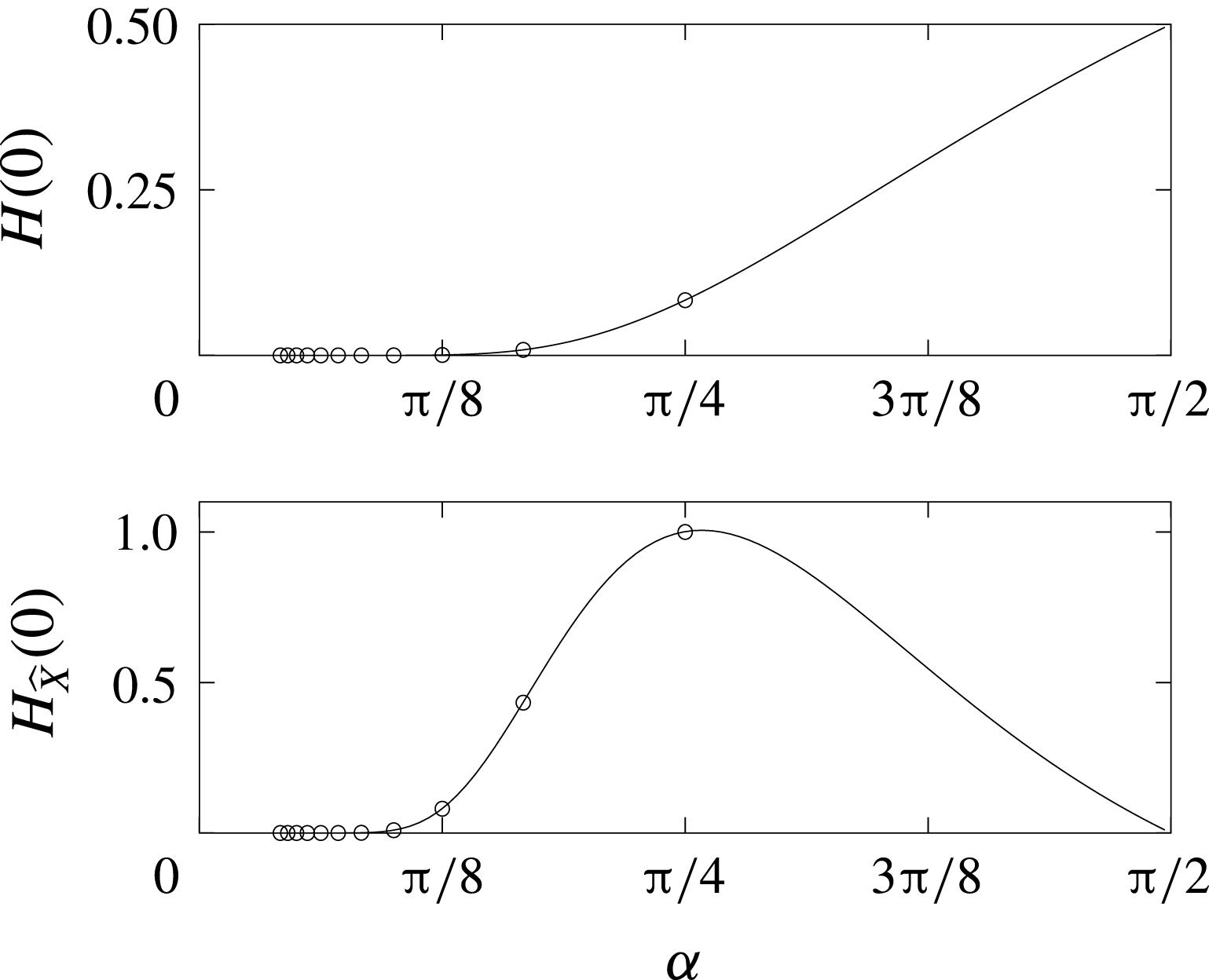
Figure 8. Numerical approximation to
![]() $H(0)$
and
$H(0)$
and
![]() $H_{\widehat{X}}(0)$
for
$H_{\widehat{X}}(0)$
for
![]() $(\text{PBVP})^{+}$
. Exact values for
$(\text{PBVP})^{+}$
. Exact values for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots ,10$
) (via (4.32)) are shown as circles.
$n=1,2,\ldots ,10$
) (via (4.32)) are shown as circles.
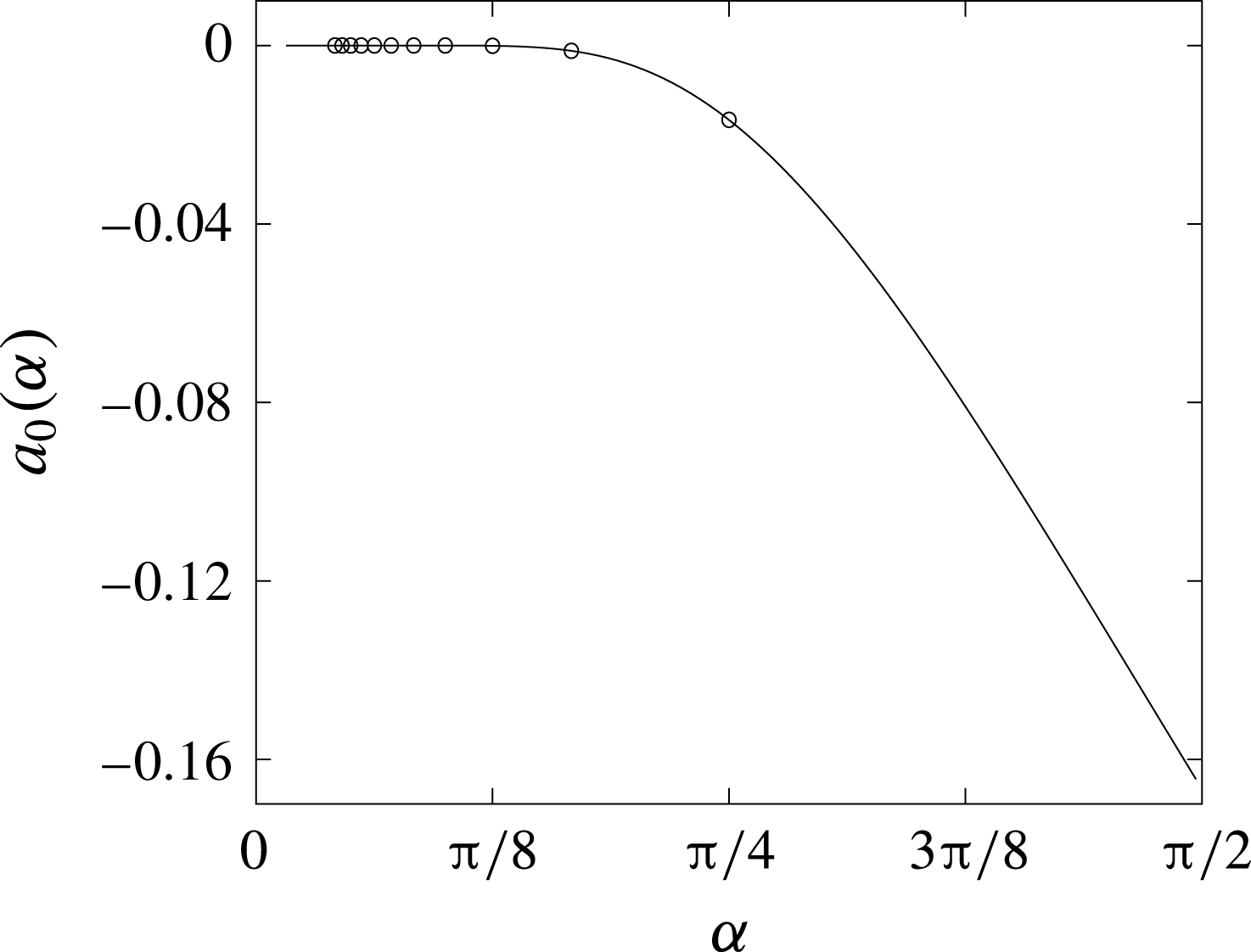
Figure 9. Numerical approximation to the near-field constant
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
for
$a_{0}(\unicode[STIX]{x1D6FC})$
for
![]() $(\text{PBVP})^{+}$
. Exact solutions for
$(\text{PBVP})^{+}$
. Exact solutions for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots ,10$
) (4.34) are shown as circles.
$n=1,2,\ldots ,10$
) (4.34) are shown as circles.
Figure 9 shows a plot of the numerically determined near-field constant
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
, as given in (4.27), for
$a_{0}(\unicode[STIX]{x1D6FC})$
, as given in (4.27), for
![]() $(\text{PBVP})^{+}$
against
$(\text{PBVP})^{+}$
against
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, where the exact values for
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, where the exact values for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
in (4.34) are shown as circles. The numerical evidence shows that
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
in (4.34) are shown as circles. The numerical evidence shows that
![]() $a_{0}(\unicode[STIX]{x1D6FC})<0$
for all
$a_{0}(\unicode[STIX]{x1D6FC})<0$
for all
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, with
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, with
![]() $a_{0}(\unicode[STIX]{x1D6FC})\rightarrow 0$
as
$a_{0}(\unicode[STIX]{x1D6FC})\rightarrow 0$
as
![]() $\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
, that
$\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
, that
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
is monotonically decreasing as
$a_{0}(\unicode[STIX]{x1D6FC})$
is monotonically decreasing as
![]() $\unicode[STIX]{x1D6FC}$
increases and that
$\unicode[STIX]{x1D6FC}$
increases and that
![]() $a_{0}(\unicode[STIX]{x1D6FC})\rightarrow -1/6$
as
$a_{0}(\unicode[STIX]{x1D6FC})\rightarrow -1/6$
as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. The numerical solution indicates that
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. The numerical solution indicates that
![]() $(\text{PBVP})^{+}$
has a unique solution, which we denote by
$(\text{PBVP})^{+}$
has a unique solution, which we denote by
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}(\widehat{R},\unicode[STIX]{x1D703})$
, with a corresponding solution for
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}(\widehat{R},\unicode[STIX]{x1D703})$
, with a corresponding solution for
![]() $H$
, given from (4.19), which we denote by
$H$
, given from (4.19), which we denote by
![]() $H=H_{\unicode[STIX]{x1D6FC}}^{+}(\widehat{X})$
. It follows from (4.27)–(4.29) that
$H=H_{\unicode[STIX]{x1D6FC}}^{+}(\widehat{X})$
. It follows from (4.27)–(4.29) that
with
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
as given in figure 9, and the regularity conditions (4.26) are satisfied in the inner region; thus, no further asymptotic regions will be required in the structure to [IBVP] as
$a_{0}(\unicode[STIX]{x1D6FC})$
as given in figure 9, and the regularity conditions (4.26) are satisfied in the inner region; thus, no further asymptotic regions will be required in the structure to [IBVP] as
![]() $t\rightarrow 0^{+}$
in this case.
$t\rightarrow 0^{+}$
in this case.
4.4 Numerical results for
 $(PBVP)^{-}$
$(PBVP)^{-}$
We now examine the results obtained by solving
![]() $\text{(PBVP)}^{-}$
numerically. The numerical solution reveals a rapidly changing character around values
$\text{(PBVP)}^{-}$
numerically. The numerical solution reveals a rapidly changing character around values
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
), with
$n=1,2,\ldots$
), with
![]() $\unicode[STIX]{x1D6FC}_{n}^{\ast }$
having been determined from the numerical solution, the values of which indicate that
$\unicode[STIX]{x1D6FC}_{n}^{\ast }$
having been determined from the numerical solution, the values of which indicate that
where
![]() $\unicode[STIX]{x1D6FC}_{0}$
is taken as
$\unicode[STIX]{x1D6FC}_{0}$
is taken as
![]() $\unicode[STIX]{x03C0}/2$
. Following the approach used to solve
$\unicode[STIX]{x03C0}/2$
. Following the approach used to solve
![]() $\text{(PBVP)}^{+}$
, we first set the numerical parameters, choosing
$\text{(PBVP)}^{+}$
, we first set the numerical parameters, choosing
![]() $\unicode[STIX]{x1D716}=10^{-4}$
. For the angles
$\unicode[STIX]{x1D716}=10^{-4}$
. For the angles
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
), where we have exact solutions, we implement the far-field asymptotic form (4.25) at
$n=1,2,\ldots$
), where we have exact solutions, we implement the far-field asymptotic form (4.25) at
![]() $\widehat{R}=10$
, which must then be increased as we approach each
$\widehat{R}=10$
, which must then be increased as we approach each
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
). As with the solution to
$n=1,2,\ldots$
). As with the solution to
![]() $\text{(PBVP)}^{+}$
, we begin by choosing angles
$\text{(PBVP)}^{+}$
, we begin by choosing angles
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, numerically solve
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, numerically solve
![]() $\text{(PBVP)}^{-}$
using a finite difference scheme for each angle, and plot the level curves of
$\text{(PBVP)}^{-}$
using a finite difference scheme for each angle, and plot the level curves of
![]() $\unicode[STIX]{x1D6F7}$
in figure 10 and
$\unicode[STIX]{x1D6F7}$
in figure 10 and
![]() $H$
in figure 11.
$H$
in figure 11.
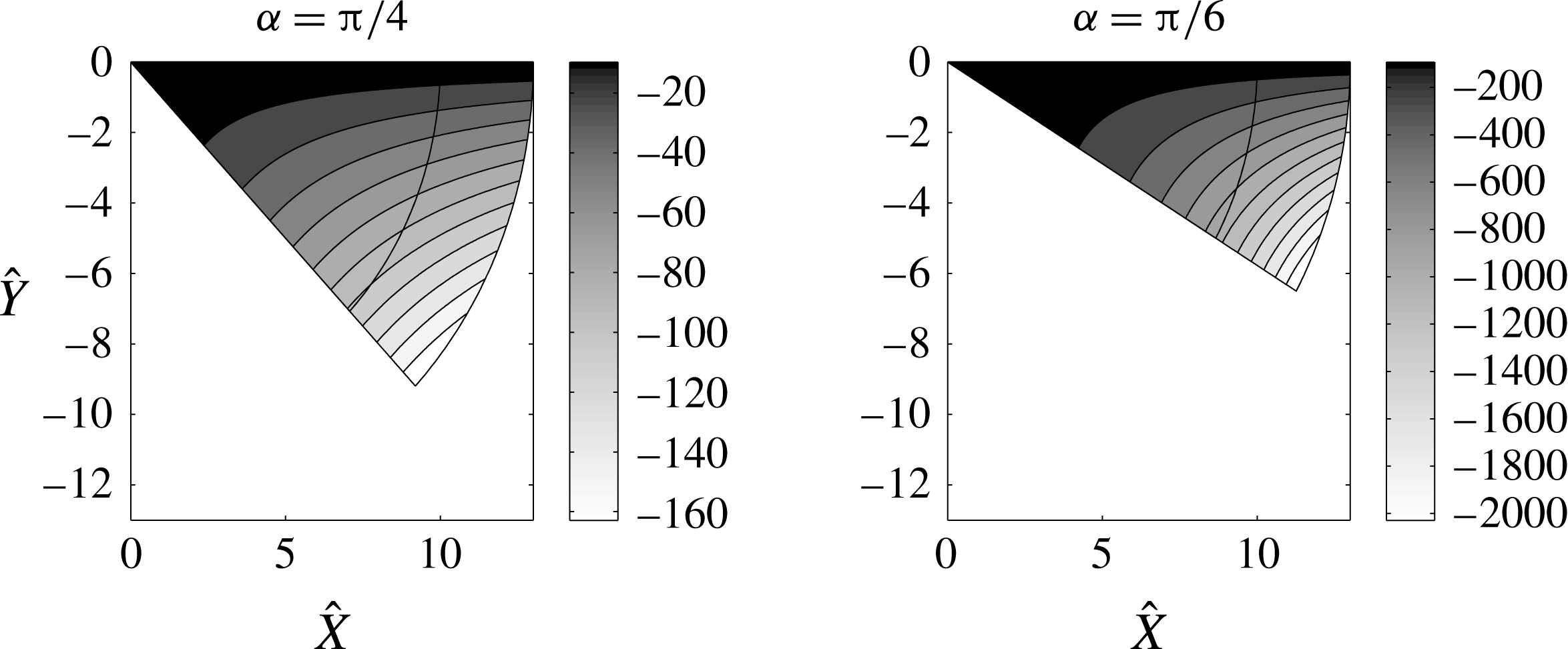
Figure 10. Contours of
![]() $\unicode[STIX]{x1D6F7}$
for the numerical solution of
$\unicode[STIX]{x1D6F7}$
for the numerical solution of
![]() $\text{(PBVP)}^{-}$
when
$\text{(PBVP)}^{-}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a line shows
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a line shows
![]() $\widehat{R}=10$
, after which the far-field asymptotic form (4.25) is plotted.
$\widehat{R}=10$
, after which the far-field asymptotic form (4.25) is plotted.
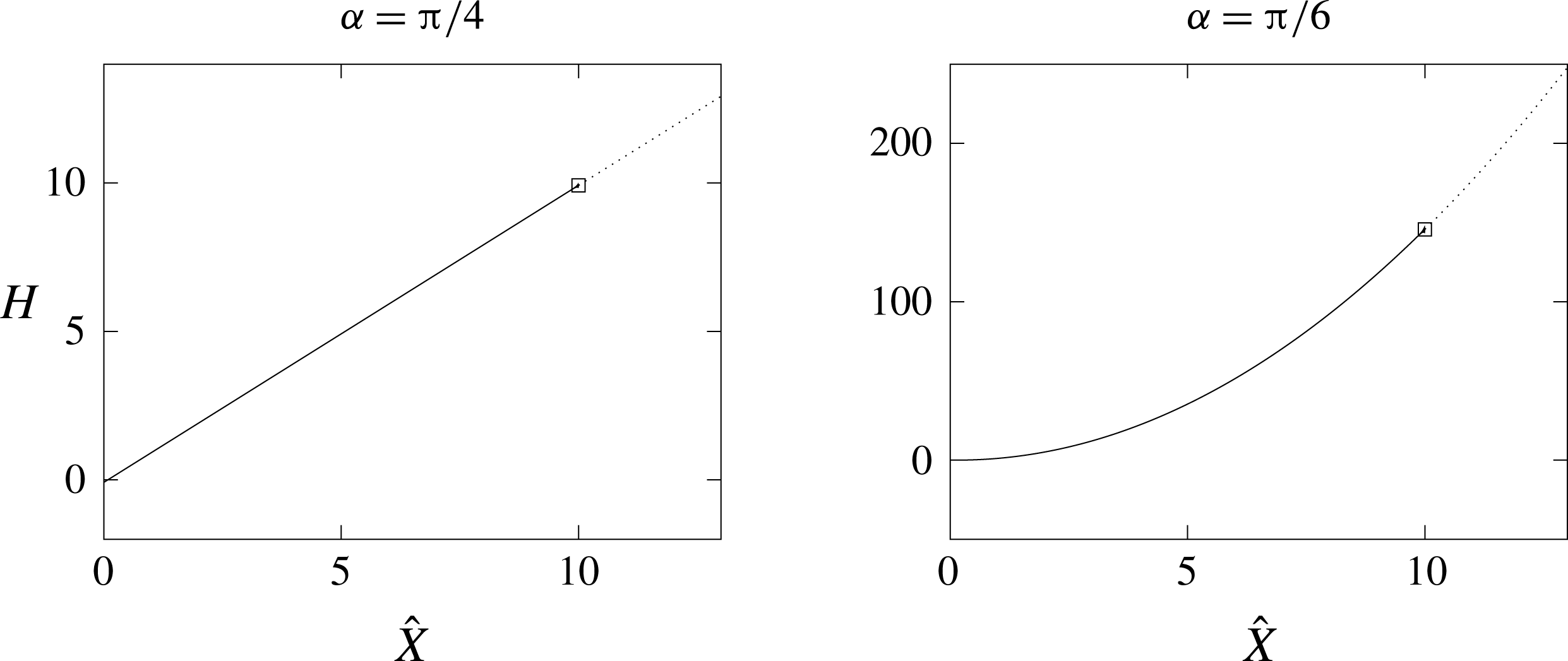
Figure 11. Graphs of
![]() $H$
for the numerical solution of
$H$
for the numerical solution of
![]() $\text{(PBVP)}^{-}$
when
$\text{(PBVP)}^{-}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a square shows
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, a square shows
![]() $\widehat{R}=10$
, after which the far-field asymptotic form (4.20) is plotted.
$\widehat{R}=10$
, after which the far-field asymptotic form (4.20) is plotted.
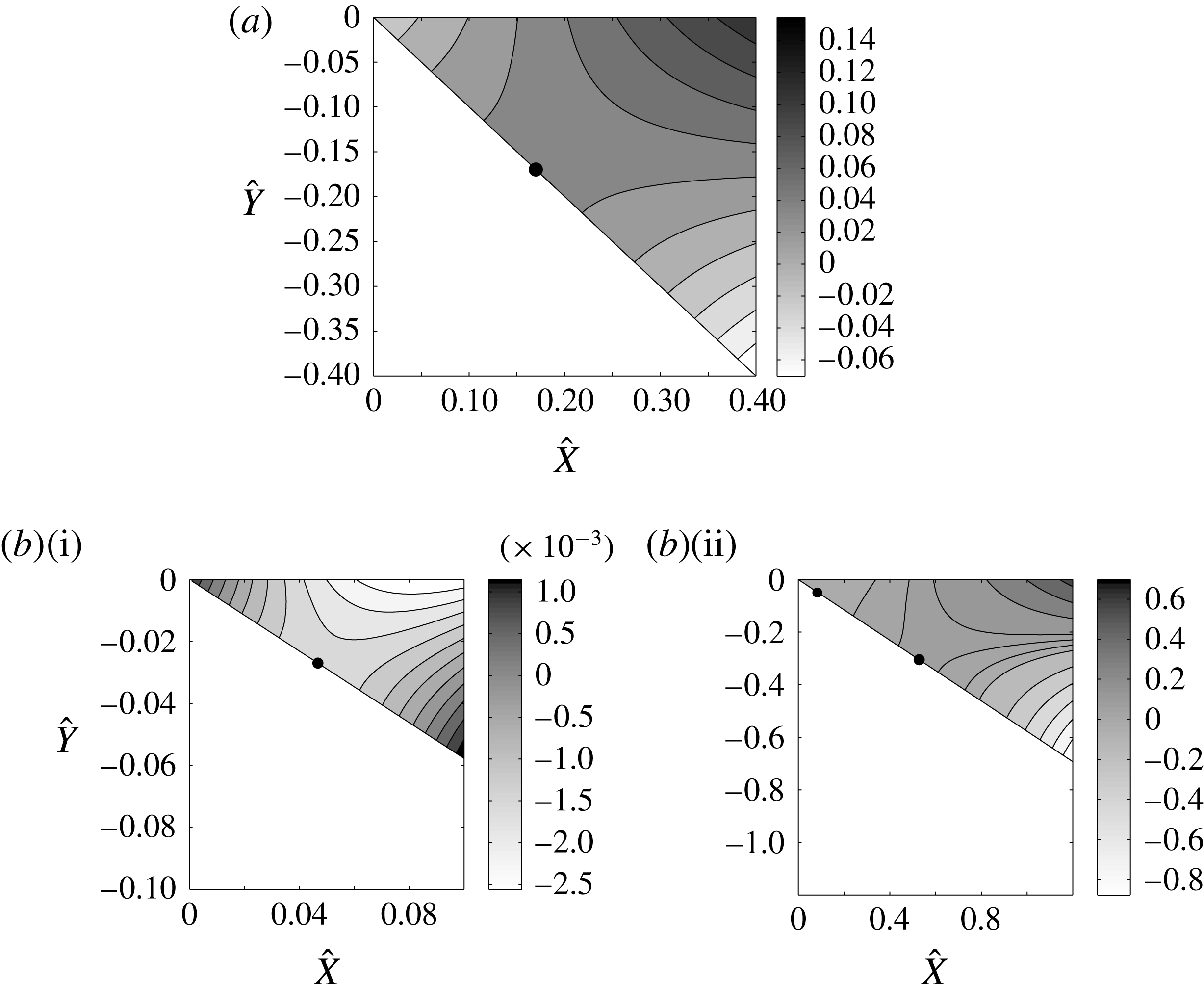
Figure 12. Contours of
![]() $\unicode[STIX]{x1D6F7}$
for the numerical solution of
$\unicode[STIX]{x1D6F7}$
for the numerical solution of
![]() $\text{(PBVP)}^{-}$
close to the tip of the wedge when (a)
$\text{(PBVP)}^{-}$
close to the tip of the wedge when (a)
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and (b)
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and (b)
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. The stationary points are marked with a dot. It should be noted that the scales in (b)(i) and (b)(ii) have been chosen to show clearly the contours of
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. The stationary points are marked with a dot. It should be noted that the scales in (b)(i) and (b)(ii) have been chosen to show clearly the contours of
![]() $\unicode[STIX]{x1D6F7}$
close to each of the stationary points.
$\unicode[STIX]{x1D6F7}$
close to each of the stationary points.
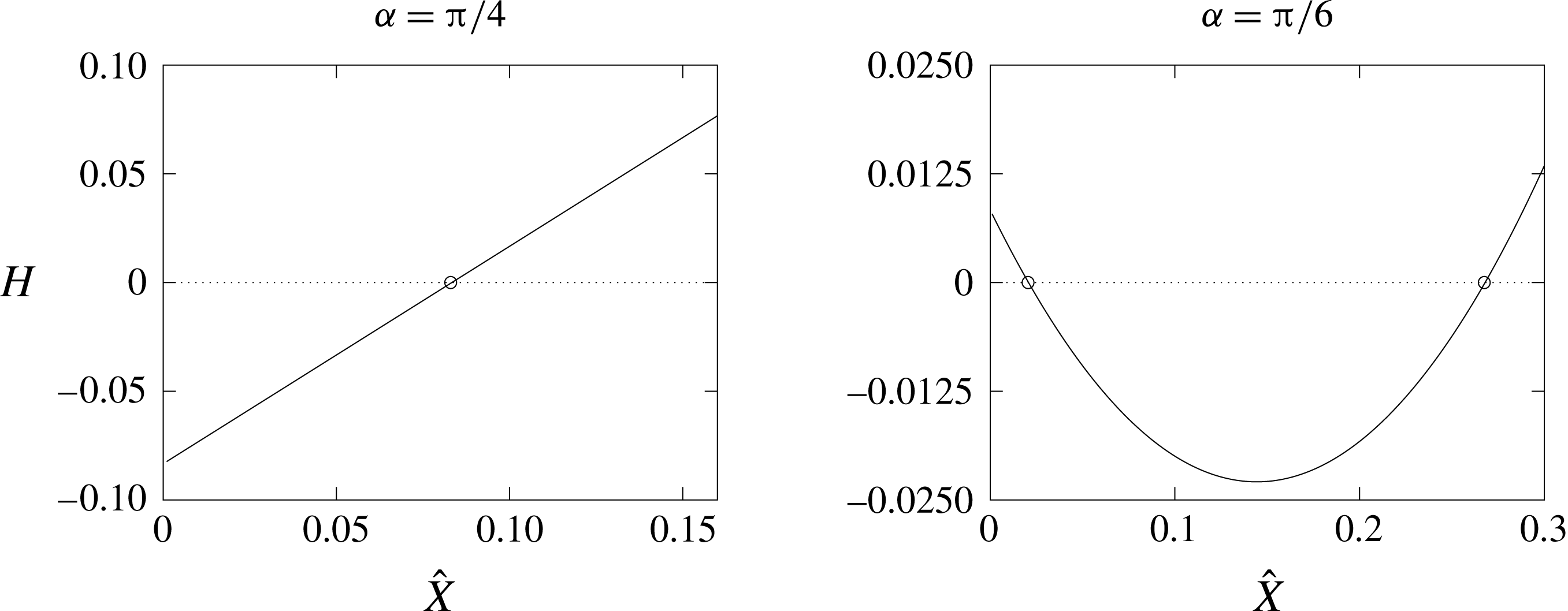
Figure 13. Graphs of
![]() $H$
close to the tip of the wedge for the numerical solution of
$H$
close to the tip of the wedge for the numerical solution of
![]() $\text{(PBVP)}^{-}$
when
$\text{(PBVP)}^{-}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, circles highlight the locations of zeros of
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. In each plot, circles highlight the locations of zeros of
![]() $H$
.
$H$
.
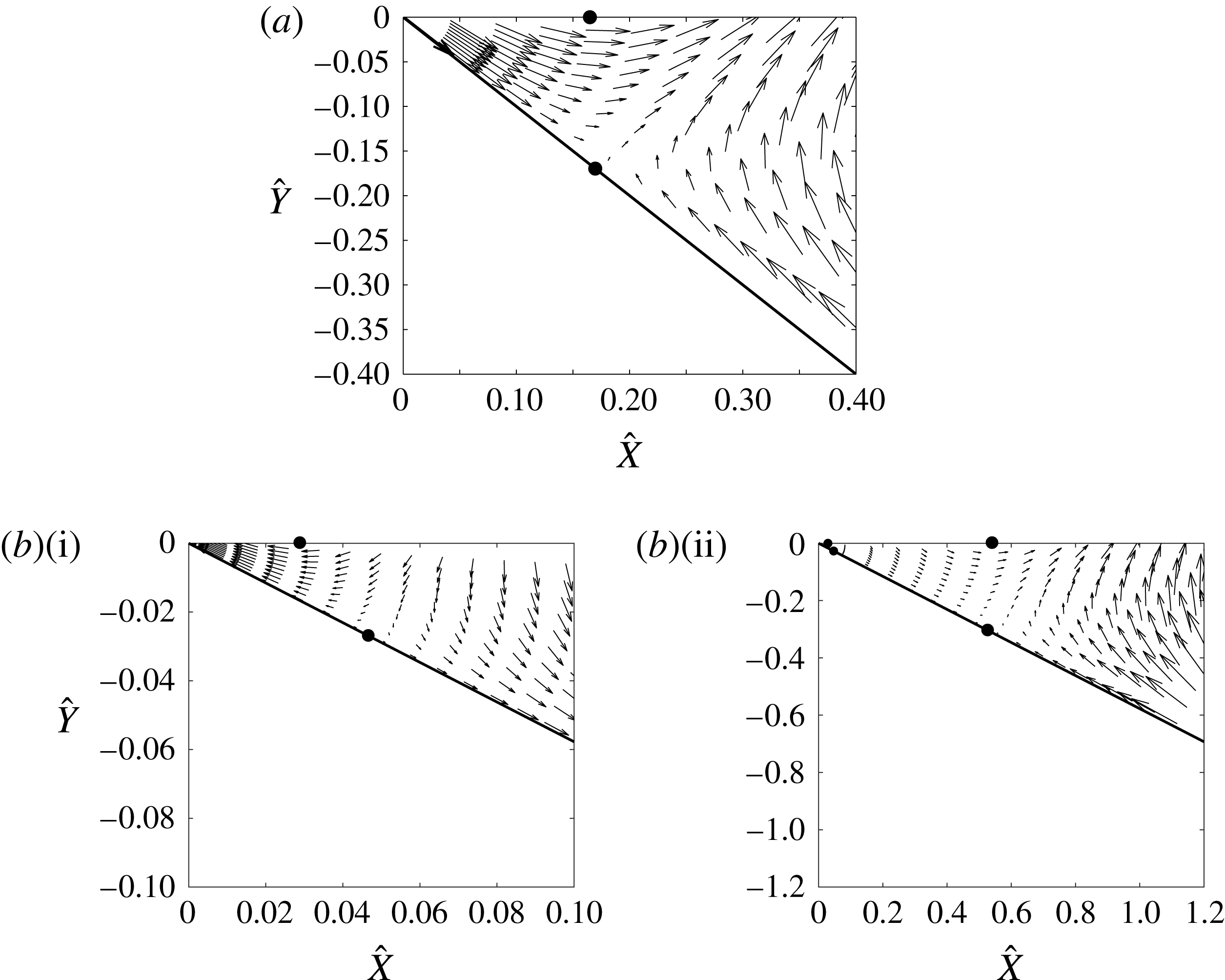
Figure 14. The vector field
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
for the numerical solution of
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
for the numerical solution of
![]() $\text{(PBVP)}^{-}$
close to the tip of the wedge when (a)
$\text{(PBVP)}^{-}$
close to the tip of the wedge when (a)
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and (b)
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and (b)
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. The reversal points are marked with a dot. It should be noted that the scales in (b) have been chosen to show clearly the vector field
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. The reversal points are marked with a dot. It should be noted that the scales in (b) have been chosen to show clearly the vector field
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
close to each of the reversal points.
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
close to each of the reversal points.
It is of interest to examine the structure of the level curves of
![]() $\unicode[STIX]{x1D6F7}$
, in both cases
$\unicode[STIX]{x1D6F7}$
, in both cases
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, closer to the tip of the wedge. These are shown in figure 12. For
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, closer to the tip of the wedge. These are shown in figure 12. For
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
, figure 12(a) reveals a stationary point (saddle) for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
, figure 12(a) reveals a stationary point (saddle) for
![]() $\unicode[STIX]{x1D6F7}$
on the boundary
$\unicode[STIX]{x1D6F7}$
on the boundary
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$
when
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$
when
![]() $\widehat{R}\approx 0.24$
. This accompanies a reversal in
$\widehat{R}\approx 0.24$
. This accompanies a reversal in
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
on
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
on
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$
when the stationary point is crossed, and a change in sign of
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$
when the stationary point is crossed, and a change in sign of
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
![]() $\unicode[STIX]{x1D703}=0$
, as can be seen in figure 14(a), where the vector field
$\unicode[STIX]{x1D703}=0$
, as can be seen in figure 14(a), where the vector field
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
is plotted for
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
is plotted for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. For
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
. For
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, figure 12(b) reveals that there are now two stationary points (both saddles) for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, figure 12(b) reveals that there are now two stationary points (both saddles) for
![]() $\unicode[STIX]{x1D6F7}$
on the boundary
$\unicode[STIX]{x1D6F7}$
on the boundary
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/6$
, when
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/6$
, when
![]() $\widehat{R}\approx 0.054$
and
$\widehat{R}\approx 0.054$
and
![]() $\widehat{R}\approx 0.61$
. Consequently, there are now two reversals in
$\widehat{R}\approx 0.61$
. Consequently, there are now two reversals in
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
on
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}$
on
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/6$
, and two associated sign changes in
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/6$
, and two associated sign changes in
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
![]() $\unicode[STIX]{x1D703}=0$
, as can be seen in figure 14(b). An investigation of each of the angles
$\unicode[STIX]{x1D703}=0$
, as can be seen in figure 14(b). An investigation of each of the angles
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
) where exact solutions are available (given in (4.31)) reveals that when
$n=1,2,\ldots$
) where exact solutions are available (given in (4.31)) reveals that when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
), then
$n=1,2,\ldots$
), then
![]() $\unicode[STIX]{x1D6F7}$
has exactly
$\unicode[STIX]{x1D6F7}$
has exactly
![]() $n$
stationary points (each a saddle point) on
$n$
stationary points (each a saddle point) on
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}_{n}$
, and, consequently, there are
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}_{n}$
, and, consequently, there are
![]() $n$
sign changes in
$n$
sign changes in
![]() $\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
$\widehat{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D6F7}\boldsymbol{\cdot }\,\boldsymbol{j}$
on
![]() $\unicode[STIX]{x1D703}=0$
. Significantly, each of these sign changes leads to a zero of
$\unicode[STIX]{x1D703}=0$
. Significantly, each of these sign changes leads to a zero of
![]() $H(\widehat{X})$
in
$H(\widehat{X})$
in
![]() $\widehat{X}>0$
. Thus, when
$\widehat{X}>0$
. Thus, when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
), then
$n=1,2,\ldots$
), then
![]() $H(\widehat{X})$
has exactly
$H(\widehat{X})$
has exactly
![]() $n$
zeros in
$n$
zeros in
![]() $\widehat{X}>0$
, and
$\widehat{X}>0$
, and
![]() $H(0)$
has sign
$H(0)$
has sign
![]() $(-1)^{n}$
, with
$(-1)^{n}$
, with
![]() $H(\widehat{X})\rightarrow \infty$
as
$H(\widehat{X})\rightarrow \infty$
as
![]() $\widehat{X}\rightarrow \infty$
. Since
$\widehat{X}\rightarrow \infty$
. Since
![]() $H(\widehat{X})$
is a polynomial of degree
$H(\widehat{X})$
is a polynomial of degree
![]() $n$
, then this establishes that
$n$
, then this establishes that
![]() $H(\widehat{X})$
has exactly
$H(\widehat{X})$
has exactly
![]() $(n-1)$
turning points in
$(n-1)$
turning points in
![]() $\widehat{X}>0$
. This is illustrated in figure 13, which plots
$\widehat{X}>0$
. This is illustrated in figure 13, which plots
![]() $H(\widehat{X})$
for
$H(\widehat{X})$
for
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, close to
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
, close to
![]() $\widehat{X}=0$
. The exact solutions to
$\widehat{X}=0$
. The exact solutions to
![]() $\text{(PBVP)}^{-}$
((4.31) and (4.32)) when
$\text{(PBVP)}^{-}$
((4.31) and (4.32)) when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
are plotted in figures 15 and 16. Comparison between figures 10 and 11, and figures 15 and 16 shows excellent agreement up to the graphical scales given in the figures.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
are plotted in figures 15 and 16. Comparison between figures 10 and 11, and figures 15 and 16 shows excellent agreement up to the graphical scales given in the figures.

Figure 15. Contours of
![]() $\unicode[STIX]{x1D6F7}$
for the exact solution (4.31) of
$\unicode[STIX]{x1D6F7}$
for the exact solution (4.31) of
![]() $\text{(PBVP)}^{-}$
when
$\text{(PBVP)}^{-}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
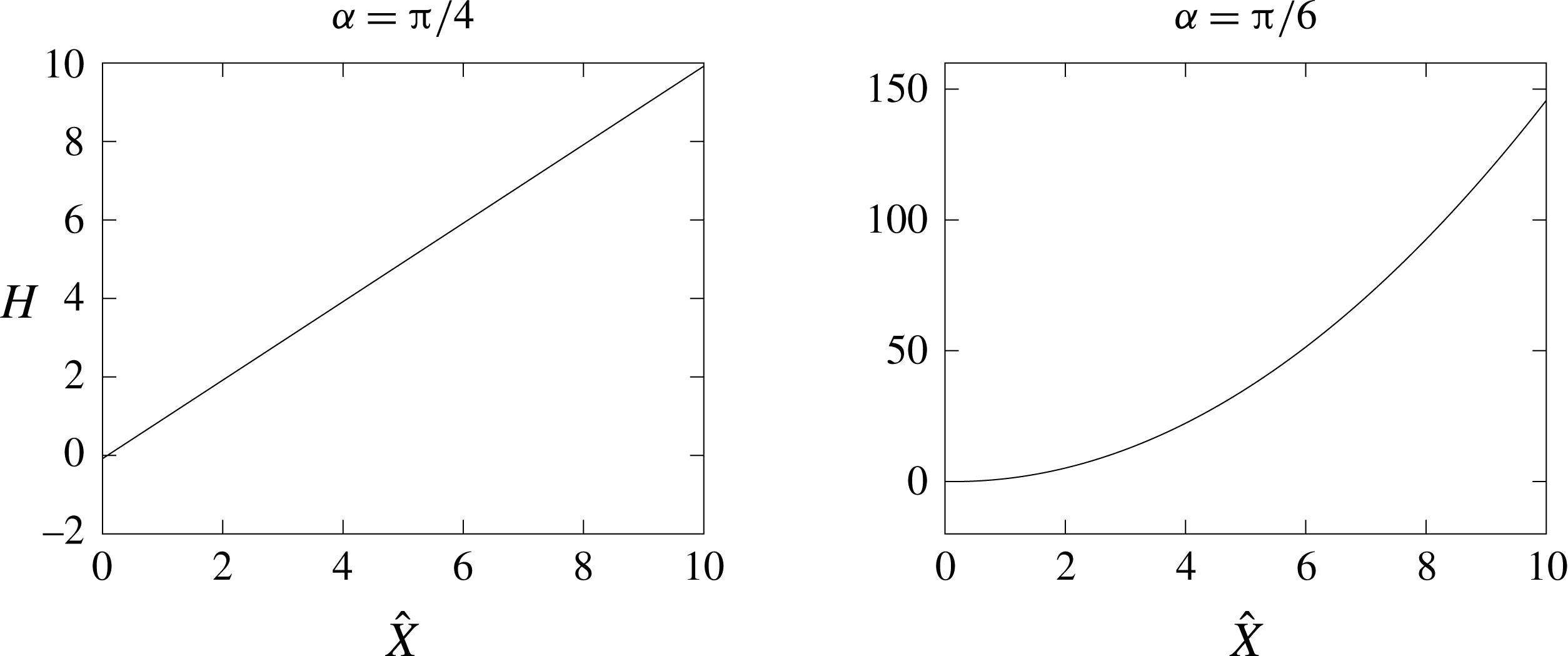
Figure 16. Graphs of
![]() $H$
for the exact solution (4.32) of
$H$
for the exact solution (4.32) of
![]() $\text{(PBVP)}^{-}$
when
$\text{(PBVP)}^{-}$
when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4$
and
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/6$
.
The near-field constant
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
, as given in (4.27) for
$a_{0}(\unicode[STIX]{x1D6FC})$
, as given in (4.27) for
![]() $\text{(PBVP)}^{-}$
, is now investigated for
$\text{(PBVP)}^{-}$
, is now investigated for
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. A careful numerical study shows, in the case of
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. A careful numerical study shows, in the case of
![]() $\text{(PBVP)}^{-}$
, that
$\text{(PBVP)}^{-}$
, that
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
has a very distinct character from that for
$a_{0}(\unicode[STIX]{x1D6FC})$
has a very distinct character from that for
![]() $\text{(PBVP)}^{+}$
, which supports our observations earlier for the cases when
$\text{(PBVP)}^{+}$
, which supports our observations earlier for the cases when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
), and the exact polynomial solution is available. Numerical agreement with the cases
$n=1,2,\ldots$
), and the exact polynomial solution is available. Numerical agreement with the cases
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=1,2,\ldots$
) is excellent up to the graphical scales given in the figures, and gives us confidence in the determination of
$n=1,2,\ldots$
) is excellent up to the graphical scales given in the figures, and gives us confidence in the determination of
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
for
$a_{0}(\unicode[STIX]{x1D6FC})$
for
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. The structure of the graph of
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. The structure of the graph of
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
for
$a_{0}(\unicode[STIX]{x1D6FC})$
for
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
is as follows.
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
is as follows.
-
(i) The constant
 $a_{0}(\unicode[STIX]{x1D6FC})$
has a sequence of pairs of near resonances, between which
$a_{0}(\unicode[STIX]{x1D6FC})$
has a sequence of pairs of near resonances, between which
 $a_{0}(\unicode[STIX]{x1D6FC})$
rapidly changes sign, vanishing at a sequence of points
$a_{0}(\unicode[STIX]{x1D6FC})$
rapidly changes sign, vanishing at a sequence of points
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
 $n=1,2,\ldots$
), which are decreasing in
$n=1,2,\ldots$
), which are decreasing in
 $n$
and approach zero as
$n$
and approach zero as
 $n\rightarrow \infty$
. Moreover,
$n\rightarrow \infty$
. Moreover,
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
 $n=1,2,\ldots$
) interlaces with
$n=1,2,\ldots$
) interlaces with
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}$
(
 $n=1,2,\ldots$
), as in (4.39), with
$n=1,2,\ldots$
), as in (4.39), with
 $\unicode[STIX]{x1D6FC}_{1}^{\ast }\approx 1.41$
. Computed values of
$\unicode[STIX]{x1D6FC}_{1}^{\ast }\approx 1.41$
. Computed values of
 $\unicode[STIX]{x1D6FC}_{n}^{\ast }$
for
$\unicode[STIX]{x1D6FC}_{n}^{\ast }$
for
 $n=2,3,\ldots ,10$
are given by
$n=2,3,\ldots ,10$
are given by
 $\unicode[STIX]{x1D6FC}_{2}^{\ast }\approx 0.739$
,
$\unicode[STIX]{x1D6FC}_{2}^{\ast }\approx 0.739$
,
 $\unicode[STIX]{x1D6FC}_{3}^{\ast }\approx 0.493$
,
$\unicode[STIX]{x1D6FC}_{3}^{\ast }\approx 0.493$
,
 $\unicode[STIX]{x1D6FC}_{4}^{\ast }\approx 0.378$
,
$\unicode[STIX]{x1D6FC}_{4}^{\ast }\approx 0.378$
,
 $\unicode[STIX]{x1D6FC}_{5}^{\ast }\approx 0.303$
,
$\unicode[STIX]{x1D6FC}_{5}^{\ast }\approx 0.303$
,
 $\unicode[STIX]{x1D6FC}_{6}^{\ast }\approx 0.251$
,
$\unicode[STIX]{x1D6FC}_{6}^{\ast }\approx 0.251$
,
 $\unicode[STIX]{x1D6FC}_{7}^{\ast }\approx 0.214$
,
$\unicode[STIX]{x1D6FC}_{7}^{\ast }\approx 0.214$
,
 $\unicode[STIX]{x1D6FC}_{8}^{\ast }\approx 0.186$
,
$\unicode[STIX]{x1D6FC}_{8}^{\ast }\approx 0.186$
,
 $\unicode[STIX]{x1D6FC}_{9}^{\ast }\approx 0.163$
,
$\unicode[STIX]{x1D6FC}_{9}^{\ast }\approx 0.163$
,
 $\unicode[STIX]{x1D6FC}_{10}^{\ast }\approx 0.146$
.
$\unicode[STIX]{x1D6FC}_{10}^{\ast }\approx 0.146$
. -
(ii) Between the near resonance pairs,
 $a_{0}(\unicode[STIX]{x1D6FC})$
is positive and monotone decreasing for
$a_{0}(\unicode[STIX]{x1D6FC})$
is positive and monotone decreasing for
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
. Subsequently,
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
. Subsequently,
 $a_{0}(\unicode[STIX]{x1D6FC})$
is positive, with a single minimum point, at values of
$a_{0}(\unicode[STIX]{x1D6FC})$
is positive, with a single minimum point, at values of
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
 $n=1,2,\ldots$
), while
$n=1,2,\ldots$
), while
 $a_{0}(\unicode[STIX]{x1D6FC})$
is negative, with a single maximum point, when
$a_{0}(\unicode[STIX]{x1D6FC})$
is negative, with a single maximum point, when
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
 $n=1,2,\ldots$
).
$n=1,2,\ldots$
).
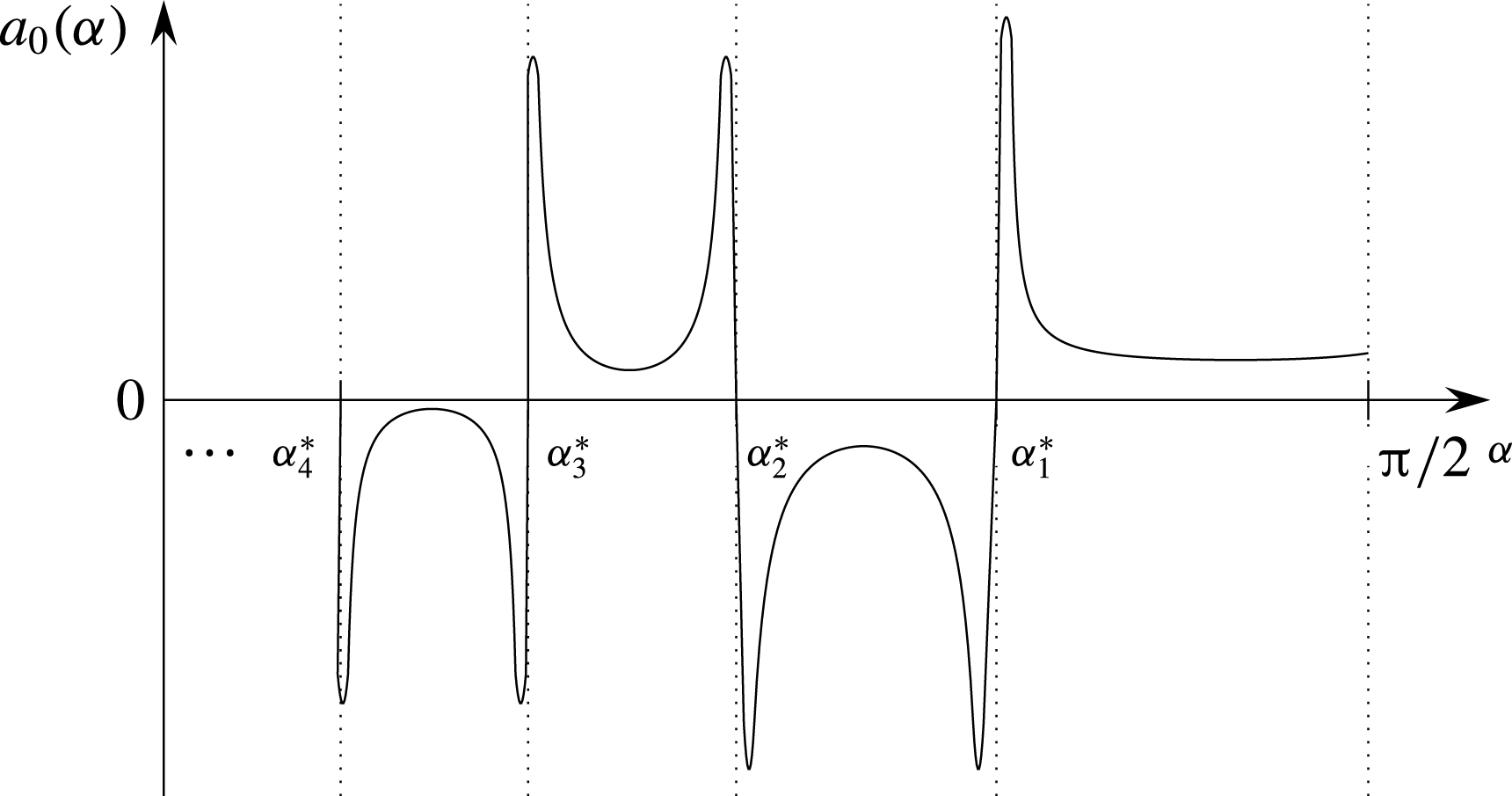
Figure 17. A qualitative sketch of the structure of
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
for
$a_{0}(\unicode[STIX]{x1D6FC})$
for
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
.
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
.
A qualitative sketch of
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
for
$a_{0}(\unicode[STIX]{x1D6FC})$
for
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
is illustrated in figure 17. Computation shows that the consecutive stationary values of
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
is illustrated in figure 17. Computation shows that the consecutive stationary values of
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
, between consecutive near resonance pairs, approach zero as
$a_{0}(\unicode[STIX]{x1D6FC})$
, between consecutive near resonance pairs, approach zero as
![]() $\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
, and
$\unicode[STIX]{x1D6FC}\rightarrow 0^{+}$
, and
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
approaches a finite positive value as
$a_{0}(\unicode[STIX]{x1D6FC})$
approaches a finite positive value as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. In addition, as each
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. In addition, as each
![]() $\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
) is crossed, with decreasing
$n=1,2,\ldots$
) is crossed, with decreasing
![]() $\unicode[STIX]{x1D6FC}$
, the number of stationary points (saddles) of
$\unicode[STIX]{x1D6FC}$
, the number of stationary points (saddles) of
![]() $\unicode[STIX]{x1D6F7}$
on
$\unicode[STIX]{x1D6F7}$
on
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}$
increases by one, and the number of zeros and turning points of
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x1D6FC}$
increases by one, and the number of zeros and turning points of
![]() $H$
in
$H$
in
![]() $\widehat{X}\geqslant 0$
increases by one. At
$\widehat{X}\geqslant 0$
increases by one. At
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
,
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
,
![]() $\unicode[STIX]{x1D6F7}$
has a stationary point (saddle) at the tip of the wedge.
$\unicode[STIX]{x1D6F7}$
has a stationary point (saddle) at the tip of the wedge.
For
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
,
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
,
![]() $\unicode[STIX]{x1D6F7}(\widehat{X},\widehat{Y})$
has no stationary points, and
$\unicode[STIX]{x1D6F7}(\widehat{X},\widehat{Y})$
has no stationary points, and
![]() $H(\widehat{X})$
has no zeros but has a single minimum point in
$H(\widehat{X})$
has no zeros but has a single minimum point in
![]() $\widehat{X}>0$
. We note that the numerical solution of
$\widehat{X}>0$
. We note that the numerical solution of
![]() $\text{(PBVP)}^{-}$
, for angles close to
$\text{(PBVP)}^{-}$
, for angles close to
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
), required increasingly large values of
$n=1,2,\ldots$
), required increasingly large values of
![]() $\widehat{R}$
to achieve suitable accuracy in the far-field boundary condition.
$\widehat{R}$
to achieve suitable accuracy in the far-field boundary condition.
Denoting the solution to
![]() $\text{(PBVP)}^{-}$
as
$\text{(PBVP)}^{-}$
as
![]() $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}(\widehat{R},\unicode[STIX]{x1D703})$
(and correspondingly
$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}(\widehat{R},\unicode[STIX]{x1D703})$
(and correspondingly
![]() $H=H_{\unicode[STIX]{x1D6FC}}^{-}(\widehat{X})$
), the behaviour close to the tip of the wedge is as follows.
$H=H_{\unicode[STIX]{x1D6FC}}^{-}(\widehat{X})$
), the behaviour close to the tip of the wedge is as follows.
For
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \}$
, it follows from (4.27)–(4.29) that
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \}$
, it follows from (4.27)–(4.29) that
For
![]() $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, it follows from (4.27)–(4.29) that
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, it follows from (4.27)–(4.29) that
with
![]() $b_{1}(\unicode[STIX]{x1D6FC}_{n}^{\ast })$
being a globally determined real constant.
$b_{1}(\unicode[STIX]{x1D6FC}_{n}^{\ast })$
being a globally determined real constant.
4.5 Summary of the solution structure to the boundary value problem (4.11)–(4.16)
We are now able to summarise the results of the previous three subsections in relation to the boundary value problem (4.11)–(4.16). We interpret these results in terms of the parameters
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
and
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
and
![]() $\unicode[STIX]{x1D707}\in \mathbb{R}$
(with
$\unicode[STIX]{x1D707}\in \mathbb{R}$
(with
![]() $\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
). We have the following.
$\unicode[STIX]{x1D707}=1+\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}$
). We have the following.
For
![]() $\unicode[STIX]{x1D707}>0$
,
$\unicode[STIX]{x1D707}>0$
,
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
![]() $(\overline{X},\overline{Y})=(0,0)$
, given by
$(\overline{X},\overline{Y})=(0,0)$
, given by
where
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}$
and
![]() $H_{\unicode[STIX]{x1D6FC}}^{+}$
have local structure given in (4.37) and (4.38) respectively.
$H_{\unicode[STIX]{x1D6FC}}^{+}$
have local structure given in (4.37) and (4.38) respectively.
For
![]() $\unicode[STIX]{x1D707}<0$
,
$\unicode[STIX]{x1D707}<0$
,
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
![]() $(\overline{X},\overline{Y})=(0,0)$
, given by
$(\overline{X},\overline{Y})=(0,0)$
, given by
where
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}$
and
![]() $H_{\unicode[STIX]{x1D6FC}}^{+}$
have local structure given in (4.40) and (4.41) respectively.
$H_{\unicode[STIX]{x1D6FC}}^{+}$
have local structure given in (4.40) and (4.41) respectively.
For
![]() $\unicode[STIX]{x1D707}<0$
,
$\unicode[STIX]{x1D707}<0$
,
![]() $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, a solution exists to the boundary value problem (4.11)–(4.16) with the required regularity (4.26) at
![]() $(\overline{X},\overline{Y})=(0,0)$
, given by
$(\overline{X},\overline{Y})=(0,0)$
, given by
where
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}$
and
![]() $H_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{+}$
have local structure given in (4.42) and (4.43) respectively.
$H_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{+}$
have local structure given in (4.42) and (4.43) respectively.
The case
![]() $\unicode[STIX]{x1D707}=0$
,
$\unicode[STIX]{x1D707}=0$
,
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
has not been treated yet. However, it is readily established (and anticipated by the coordinate scalings in (4.18)) that, in this degenerate case, the solution to the boundary value problem (4.11)–(4.16), which has the least singular behaviour at
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
has not been treated yet. However, it is readily established (and anticipated by the coordinate scalings in (4.18)) that, in this degenerate case, the solution to the boundary value problem (4.11)–(4.16), which has the least singular behaviour at
![]() $(\overline{X},\overline{Y})=(0,0)$
, is simply given by the far-field functions; that is,
$(\overline{X},\overline{Y})=(0,0)$
, is simply given by the far-field functions; that is,
4.6 Reconstructing the inner region asymptotic expansions
In this section, we reconstruct the inner region asymptotic expansions for the contact point, fluid velocity potential
![]() $\unicode[STIX]{x1D719}$
and free surface elevation
$\unicode[STIX]{x1D719}$
and free surface elevation
![]() $\unicode[STIX]{x1D702}$
in terms of the inner region coordinates
$\unicode[STIX]{x1D702}$
in terms of the inner region coordinates
![]() $\overline{X}$
,
$\overline{X}$
,
![]() $\overline{Y}$
, and then consider the behaviour close to the intersection point of the fluid free surface and the inclined accelerating plate. The corresponding details of the inner region asymptotic expansions for the dynamic fluid pressure field and the fluid velocity field are given in the appendix A. We must consider the four cases
$\overline{Y}$
, and then consider the behaviour close to the intersection point of the fluid free surface and the inclined accelerating plate. The corresponding details of the inner region asymptotic expansions for the dynamic fluid pressure field and the fluid velocity field are given in the appendix A. We must consider the four cases
![]() $\unicode[STIX]{x1D707}>0$
with
$\unicode[STIX]{x1D707}>0$
with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
,
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
,
![]() $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
,
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
,
![]() $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
![]() $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
and
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
and
![]() $\unicode[STIX]{x1D707}=0$
with
$\unicode[STIX]{x1D707}=0$
with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
separately.
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
separately.
4.6.1 The case
 $\unicode[STIX]{x1D707}>0$
with
$\unicode[STIX]{x1D707}>0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
It follows from (4.5), (4.8), (4.9), (4.17) and (4.18) that the intersection point of the plate and the fluid free surface is located at
![]() $(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(\unicode[STIX]{x1D70E}/2),Y_{p}(t)-(\unicode[STIX]{x1D70E}/2)\tan \unicode[STIX]{x1D6FC})$
, where
$(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(\unicode[STIX]{x1D70E}/2),Y_{p}(t)-(\unicode[STIX]{x1D70E}/2)\tan \unicode[STIX]{x1D6FC})$
, where
as
![]() $t\rightarrow 0^{+}$
. We then have, from (4.2), (4.3), (4.7), (4.9), (4.10) and (4.18), that
$t\rightarrow 0^{+}$
. We then have, from (4.2), (4.3), (4.7), (4.9), (4.10) and (4.18), that
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
, as
$\overline{X}\geqslant \overline{X}_{p}(t)$
, as
![]() $t\rightarrow 0^{+}$
. We recall that, in the inner region, the fluid free surface is located at
$t\rightarrow 0^{+}$
. We recall that, in the inner region, the fluid free surface is located at
![]() $Y=\unicode[STIX]{x1D702}_{I}(X,t)$
, so that in the shifted coordinates
$Y=\unicode[STIX]{x1D702}_{I}(X,t)$
, so that in the shifted coordinates
![]() $(\overline{X},\overline{Y})$
, the free surface is located at
$(\overline{X},\overline{Y})$
, the free surface is located at
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
. Then, from (4.54), the free surface in the inner region is located at
$\overline{X}\geqslant \overline{X}_{p}(t)$
. Then, from (4.54), the free surface in the inner region is located at
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
, as
$\overline{X}\geqslant \overline{X}_{p}(t)$
, as
![]() $t\rightarrow 0^{+}$
. We next have, from (4.2), (4.3), (4.6), (4.9), (4.10) and (4.18), that
$t\rightarrow 0^{+}$
. We next have, from (4.2), (4.3), (4.6), (4.9), (4.10) and (4.18), that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{Y}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{Y}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
, as
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
, as
![]() $t\rightarrow 0^{+}$
. We now consider the structure of the inner region asymptotic expansions close to the intersection point of the inclined plate and the fluid free surface when
$t\rightarrow 0^{+}$
. We now consider the structure of the inner region asymptotic expansions close to the intersection point of the inclined plate and the fluid free surface when
![]() $(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
$(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
![]() $t\rightarrow 0^{+}$
. We have, from (4.37), (4.38), (4.44) and (4.45), together with (4.52)–(4.57), that
$t\rightarrow 0^{+}$
. We have, from (4.37), (4.38), (4.44) and (4.45), together with (4.52)–(4.57), that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \times \left(1+\frac{\unicode[STIX]{x03C0}(1+\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}\overline{R}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O(\overline{R}^{2})\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{R}\ll \min (1,\unicode[STIX]{x1D707}),\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \times \left(1+\frac{\unicode[STIX]{x03C0}(1+\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}\overline{R}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O(\overline{R}^{2})\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{R}\ll \min (1,\unicode[STIX]{x1D707}),\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{I}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{(\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC})-1}\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{\unicode[STIX]{x03C0}(1-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\tan \unicode[STIX]{x1D6FC}}\overline{X}+O(\overline{X}^{2})\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{X}\ll \min (1,\unicode[STIX]{x1D707}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{I}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{(\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC})-1}\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{\unicode[STIX]{x03C0}(1-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\tan \unicode[STIX]{x1D6FC}}\overline{X}+O(\overline{X}^{2})\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{X}\ll \min (1,\unicode[STIX]{x1D707}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
in the inner asymptotic region, with
$t\rightarrow 0^{+}$
in the inner asymptotic region, with
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
and
$A_{0}(\unicode[STIX]{x1D6FC})$
and
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
as given in figures 4 and 9 respectively. We observe from (4.60) and (4.61) that, in this case, each of the inner region asymptotic expansions remain uniform up to the contact point, where
$a_{0}(\unicode[STIX]{x1D6FC})$
as given in figures 4 and 9 respectively. We observe from (4.60) and (4.61) that, in this case, each of the inner region asymptotic expansions remain uniform up to the contact point, where
![]() $(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
. Thus, the asymptotic structure as
$(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
. Thus, the asymptotic structure as
![]() $t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
$t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
We can now draw the following conclusions concerning the free surface in the inner asymptotic region.
-
(i) The contact point is located at
(4.62)as $$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
$t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
-
(ii) The free surface slope at the contact point is given by
(4.63)as $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t) & = & \displaystyle \unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)\nonumber\\ \displaystyle & = & \displaystyle t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\left(1-\frac{\unicode[STIX]{x03C0}^{2}}{\unicode[STIX]{x1D6FC}^{2}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cot \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-2}\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t) & = & \displaystyle \unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)\nonumber\\ \displaystyle & = & \displaystyle t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\left(1-\frac{\unicode[STIX]{x03C0}^{2}}{\unicode[STIX]{x1D6FC}^{2}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cot \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-2}\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.45) and (4.54)). We see that the free surface slope is positive when
$t\rightarrow 0^{+}$
(see (4.45) and (4.54)). We see that the free surface slope is positive when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$
and negative when
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$
and negative when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (1,\infty )$
. A contour plot of
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (1,\infty )$
. A contour plot of
 $\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}$
, as
$\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}$
, as
 $t\rightarrow 0^{+}$
, in the
$t\rightarrow 0^{+}$
, in the
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane (with
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane (with
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,\infty )$
), is shown in figure 18.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,\infty )$
), is shown in figure 18.
-
(iii) The free surface
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.64)as
$\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.64)as $$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=\frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\cos \unicode[STIX]{x1D6FC}H_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=\frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\cos \unicode[STIX]{x1D6FC}H_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
, for
$t\rightarrow 0^{+}$
, for
 $\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.54)). It follows from (4.64) that
$\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.54)). It follows from (4.64) that
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone increasing in
$\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone increasing in
 $\overline{X}\geqslant \overline{X}_{p}(t)$
when
$\overline{X}\geqslant \overline{X}_{p}(t)$
when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$
, while
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,1)$
, while
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone decreasing in
$\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone decreasing in
 $\overline{X}\geqslant \overline{X}_{p}(t)$
when
$\overline{X}\geqslant \overline{X}_{p}(t)$
when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (1,\infty )$
.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (1,\infty )$
.
When
![]() $\unicode[STIX]{x1D707}>1$
(
$\unicode[STIX]{x1D707}>1$
(
![]() $\unicode[STIX]{x1D70E}>0$
), examination of (A 1), (A 2) and (4.64) reveals that, to leading order in the inner asymptotic region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
$\unicode[STIX]{x1D70E}>0$
), examination of (A 1), (A 2) and (4.64) reveals that, to leading order in the inner asymptotic region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
![]() $(1-\unicode[STIX]{x1D707})\,\boldsymbol{j}$
, which drives a vertical jet close to the intersection point of the free surface and the plate of height
$(1-\unicode[STIX]{x1D707})\,\boldsymbol{j}$
, which drives a vertical jet close to the intersection point of the free surface and the plate of height
![]() $(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
. When
$(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
. When
![]() $0<\unicode[STIX]{x1D707}<1$
(
$0<\unicode[STIX]{x1D707}<1$
(
![]() $-\cot \unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D70E}<0$
), we see from (A 1), (A 2) and (4.64) that, to leading order in the inner asymptotic region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
$-\cot \unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D70E}<0$
), we see from (A 1), (A 2) and (4.64) that, to leading order in the inner asymptotic region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
![]() $(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
$(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
![]() $(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
$(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
Figure 18. Contour plot of
![]() $t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)$
as
$t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)$
as
![]() $t\rightarrow 0^{+}$
on the
$t\rightarrow 0^{+}$
on the
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane, in the case
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane, in the case
![]() $\unicode[STIX]{x1D707}>0$
.
$\unicode[STIX]{x1D707}>0$
.
4.6.2 The case
 $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
It follows from (4.5), (4.8), (4.9), (4.17) and (4.18) that the intersection point of the plate and the fluid free surface is located at
![]() $(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(1/2)\unicode[STIX]{x1D70E},Y_{p}(t)-(1/2)\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC})$
, with
$(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(1/2)\unicode[STIX]{x1D70E},Y_{p}(t)-(1/2)\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC})$
, with
as
![]() $t\rightarrow 0^{+}$
. We then have, from (4.2), (4.3), (4.7), (4.9), (4.10) and (4.18), that
$t\rightarrow 0^{+}$
. We then have, from (4.2), (4.3), (4.7), (4.9), (4.10) and (4.18), that
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
, as
$\overline{X}\geqslant \overline{X}_{p}(t)$
, as
![]() $t\rightarrow 0^{+}$
. We now have, from (4.55) and (4.67), that in the shifted coordinates
$t\rightarrow 0^{+}$
. We now have, from (4.55) and (4.67), that in the shifted coordinates
![]() $(\overline{X},\overline{Y})$
, the free surface in the inner region is located at
$(\overline{X},\overline{Y})$
, the free surface in the inner region is located at
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
, as
$\overline{X}\geqslant \overline{X}_{p}(t)$
, as
![]() $t\rightarrow 0^{+}$
. We next have, from (4.2), (4.3), (4.6), (4.9), (4.10) and (4.18), that
$t\rightarrow 0^{+}$
. We next have, from (4.2), (4.3), (4.6), (4.9), (4.10) and (4.18), that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{Y}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\nonumber\\ \displaystyle & & \displaystyle \times \cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{Y}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\nonumber\\ \displaystyle & & \displaystyle \times \cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
for
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
, as
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
, as
![]() $t\rightarrow 0^{+}$
. We now consider the structure of the inner region asymptotic expansions close to the intersection point of the inclined plate and the fluid free surface when
$t\rightarrow 0^{+}$
. We now consider the structure of the inner region asymptotic expansions close to the intersection point of the inclined plate and the fluid free surface when
![]() $(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
$(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
as
![]() $t\rightarrow 0^{+}$
. We have, from (4.40), (4.41), (4.46) and (4.47), together with (4.65)–(4.69), that
$t\rightarrow 0^{+}$
. We have, from (4.40), (4.41), (4.46) and (4.47), together with (4.65)–(4.69), that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \times \left(1+\frac{\unicode[STIX]{x03C0}(1+\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}\overline{R}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O(\overline{R}^{2})\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{R}\ll \min (1,\unicode[STIX]{x1D707}),\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle (\unicode[STIX]{x1D707}-1)\left[\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{6}(2-\unicode[STIX]{x1D707})\right]+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \times \left(1+\frac{\unicode[STIX]{x03C0}(1+\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\sin \unicode[STIX]{x1D6FC}}\overline{R}\cos (\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+O(\overline{R}^{2})\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{R}\ll \min (1,\unicode[STIX]{x1D707}),\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{I}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{(\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC})-1}\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{\unicode[STIX]{x03C0}(1-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\tan \unicode[STIX]{x1D6FC}}\overline{X}+O(\overline{X}^{2})\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{X}\ll \min (1,\unicode[STIX]{x1D707}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{I}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{(\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC})-1}\nonumber\\ \displaystyle & & \displaystyle \times \left(1-\frac{\unicode[STIX]{x03C0}(1-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})}{\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}\tan \unicode[STIX]{x1D6FC}}\overline{X}+O(\overline{X}^{2})\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\quad \text{for}~0<\overline{X}\ll \min (1,\unicode[STIX]{x1D707}),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
in the inner asymptotic region, with
$t\rightarrow 0^{+}$
in the inner asymptotic region, with
![]() $A_{0}(\unicode[STIX]{x1D6FC})$
and
$A_{0}(\unicode[STIX]{x1D6FC})$
and
![]() $a_{0}(\unicode[STIX]{x1D6FC})$
as given in figures 4 and 9 respectively. We observe from (4.72) and (4.73) that, in this case, each of the inner region asymptotic expansions remains uniform up to the contact point, where
$a_{0}(\unicode[STIX]{x1D6FC})$
as given in figures 4 and 9 respectively. We observe from (4.72) and (4.73) that, in this case, each of the inner region asymptotic expansions remains uniform up to the contact point, where
![]() $(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
. Thus, the asymptotic structure as
$(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
. Thus, the asymptotic structure as
![]() $t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
$t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
We can now draw the following conclusions concerning the free surface in the inner asymptotic region.
-
(i) The contact point is located at
(4.74)as $$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
$t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
-
(ii) The free surface slope at the contact point is given by
(4.75)as $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t) & = & \displaystyle \unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)\nonumber\\ \displaystyle & = & \displaystyle t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\left(1-\frac{\unicode[STIX]{x03C0}^{2}}{\unicode[STIX]{x1D6FC}^{2}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cot \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-2}\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t) & = & \displaystyle \unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)\nonumber\\ \displaystyle & = & \displaystyle t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\left(1-\frac{\unicode[STIX]{x03C0}^{2}}{\unicode[STIX]{x1D6FC}^{2}}\right)A_{0}(\unicode[STIX]{x1D6FC})a_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cot \unicode[STIX]{x1D6FC}\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-2}\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.47) and (4.67)). We see that the free surface slope is positive when
$t\rightarrow 0^{+}$
(see (4.47) and (4.67)). We see that the free surface slope is positive when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })\times (-\infty ,0)$
(
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })\times (-\infty ,0)$
(
 $n=1,2,\ldots$
) and negative when
$n=1,2,\ldots$
) and negative when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })\times (-\infty ,0)$
(
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })\times (-\infty ,0)$
(
 $n=1,2,\ldots$
) and
$n=1,2,\ldots$
) and
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)\times (-\infty ,0)$
. A contour plot of
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)\times (-\infty ,0)$
. A contour plot of
 $\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}$
, as
$\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}$
, as
 $t\rightarrow 0^{+}$
, in the
$t\rightarrow 0^{+}$
, in the
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane (with
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane (with
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (-\infty ,0)$
), is shown in figure 19.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (-\infty ,0)$
), is shown in figure 19.
-
(iii) The free surface
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.76)as
$\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.76)as $$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=\frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2/\unicode[STIX]{x1D6FC}-1}\cos \unicode[STIX]{x1D6FC}H_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=\frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2/\unicode[STIX]{x1D6FC}-1}\cos \unicode[STIX]{x1D6FC}H_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
, for
$t\rightarrow 0^{+}$
, for
 $\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.67)). It follows from (4.76) that
$\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.67)). It follows from (4.76) that
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is initially decreasing, with a single turning point for
$\unicode[STIX]{x1D702}(\overline{X},t)$
is initially decreasing, with a single turning point for
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
. For
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
. For
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{c}^{\ast },\unicode[STIX]{x1D6FC}_{1}^{\ast })$
,
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{c}^{\ast },\unicode[STIX]{x1D6FC}_{1}^{\ast })$
,
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is initially increasing, with two turning points. For
$\unicode[STIX]{x1D702}(\overline{X},t)$
is initially increasing, with two turning points. For
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{c}^{\ast }]$
,
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{c}^{\ast }]$
,
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone increasing. For
$\unicode[STIX]{x1D702}(\overline{X},t)$
is monotone increasing. For
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
 $n=1,2,\ldots$
),
$n=1,2,\ldots$
),
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is initially decreasing and has
$\unicode[STIX]{x1D702}(\overline{X},t)$
is initially decreasing and has
 $(2n-1)$
turning points. Lastly, for
$(2n-1)$
turning points. Lastly, for
 $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
 $n=2,3,\ldots$
),
$n=2,3,\ldots$
),
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is initially increasing and has
$\unicode[STIX]{x1D702}(\overline{X},t)$
is initially increasing and has
 $(2n-2)$
turning points.
$(2n-2)$
turning points.
When
![]() $\unicode[STIX]{x1D707}<0$
(
$\unicode[STIX]{x1D707}<0$
(
![]() $\unicode[STIX]{x1D70E}<-\cot \unicode[STIX]{x1D6FC}$
) with
$\unicode[STIX]{x1D70E}<-\cot \unicode[STIX]{x1D6FC}$
) with
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, examination of (A 1), (A 4) and (4.76) reveals that, to leading order in the inner region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, examination of (A 1), (A 4) and (4.76) reveals that, to leading order in the inner region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
![]() $(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
$(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
![]() $(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
$(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
Figure 19. Contour plots of
![]() $t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)$
as
$t^{2-\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)$
as
![]() $t\rightarrow 0^{+}$
on the
$t\rightarrow 0^{+}$
on the
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane in the case
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})$
plane in the case
![]() $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC})$
and
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{n+1}^{\ast },\unicode[STIX]{x1D6FC}_{n}^{\ast })$
(
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{n+1}^{\ast },\unicode[STIX]{x1D6FC}_{n}^{\ast })$
(
![]() $n=1,2,\ldots ,5$
).
$n=1,2,\ldots ,5$
).
4.6.3 The case
 $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
 $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
It follows from (4.5), (4.8), (4.9), (4.17) and (4.18) that the intersection point of the plate and the fluid free surface is located at
![]() $(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(1/2)\unicode[STIX]{x1D70E},Y_{p}(t)-(1/2)\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast })$
, with the expressions for
$(\overline{X},\overline{Y})=(\overline{X}_{p}(t),\overline{Y}_{p}(t))=(X_{p}(t)+(1/2)\unicode[STIX]{x1D70E},Y_{p}(t)-(1/2)\unicode[STIX]{x1D70E}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast })$
, with the expressions for
![]() $\overline{X}_{p}(t)$
,
$\overline{X}_{p}(t)$
,
![]() $\overline{Y}_{p}(t)$
following precisely those in (4.65) and (4.66), with
$\overline{Y}_{p}(t)$
following precisely those in (4.65) and (4.66), with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
. Similarly, the expressions for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
. Similarly, the expressions for
![]() $\unicode[STIX]{x1D702}_{I}(\overline{X},t)$
,
$\unicode[STIX]{x1D702}_{I}(\overline{X},t)$
,
![]() $\overline{Y}_{I}(\overline{X},t)$
and
$\overline{Y}_{I}(\overline{X},t)$
and
![]() $\unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t)$
follow from (4.67)–(4.69), with
$\unicode[STIX]{x1D719}_{I}(\overline{X},\overline{Y},t)$
follow from (4.67)–(4.69), with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
.
We now consider the structure of the inner region asymptotic expansions close to the intersection point of the inclined plate and the fluid free surface when
![]() $(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2})$
as
$(\overline{X},\overline{Y})=O((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2})$
as
![]() $t\rightarrow 0^{+}$
. We have, from (4.42), (4.43), (4.48) and (4.49) (recalling that
$t\rightarrow 0^{+}$
. We have, from (4.42), (4.43), (4.48) and (4.49) (recalling that
![]() $a_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })=0$
),
$a_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })=0$
),
as
![]() $t\rightarrow 0^{+}$
in the inner asymptotic region. We observe from (4.78) and (4.79) that, in this case, each of the inner region asymptotic expansions remains uniform up to the contact point, where
$t\rightarrow 0^{+}$
in the inner asymptotic region. We observe from (4.78) and (4.79) that, in this case, each of the inner region asymptotic expansions remains uniform up to the contact point, where
![]() $(\overline{X},\overline{Y})=o((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2})$
. Thus, the asymptotic structure as
$(\overline{X},\overline{Y})=o((-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2})$
. Thus, the asymptotic structure as
![]() $t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
$t\rightarrow 0^{+}$
, of the solution to [IBVP], is complete in this case.
We can now draw the following conclusions concerning the free surface in the inner asymptotic region.
-
(i) The contact point is located at
(4.80)as $$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC}_{n}^{\ast },1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}),\end{eqnarray}$$
$$\begin{eqnarray}(\overline{x},y)={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D707}-1)t^{2}(-\cot \unicode[STIX]{x1D6FC}_{n}^{\ast },1)+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
$t\rightarrow 0^{+}$
(see (4.1), (4.5) and (4.8)).
-
(ii) The free surface slope at the contact point is given by
(4.81)as $$\begin{eqnarray}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)=\unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)=o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)=\unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)=o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
(see (4.49) and (4.67)).
$t\rightarrow 0^{+}$
(see (4.49) and (4.67)).
-
(iii) The free surface
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.82)as
$\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.82)as $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2/\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }H_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D702}(\overline{X},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)t^{2}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2/\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }H_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
, for
$t\rightarrow 0^{+}$
, for
 $\overline{X}\geqslant \overline{X}_{p}(t)$
.
$\overline{X}\geqslant \overline{X}_{p}(t)$
.
When
![]() $\unicode[STIX]{x1D707}<0$
(
$\unicode[STIX]{x1D707}<0$
(
![]() $\unicode[STIX]{x1D70E}<-\cot \unicode[STIX]{x1D6FC}_{n}^{\ast }$
) with
$\unicode[STIX]{x1D70E}<-\cot \unicode[STIX]{x1D6FC}_{n}^{\ast }$
) with
![]() $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, examination of (A 1), (A 6) and (4.82) reveals that, to leading order in the inner region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
, examination of (A 1), (A 6) and (4.82) reveals that, to leading order in the inner region, the acceleration of the inclined plate induces a constant vertical dynamic pressure gradient of
![]() $(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
$(1-\unicode[STIX]{x1D707})\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
![]() $(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
$(1/2)t^{2}(\unicode[STIX]{x1D707}-1)$
.
4.6.4 The case
 $\unicode[STIX]{x1D707}=0$
with
$\unicode[STIX]{x1D707}=0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
As discussed in § 4.5, it is readily established that in this degenerate case, the solution to the boundary value problem (4.11)–(4.16), which has the least singular behaviour at
![]() $(\overline{X},\overline{Y})=(0,0)$
, is simply given by the far-field functions. In this case we have, from (4.50) and (4.51), that
$(\overline{X},\overline{Y})=(0,0)$
, is simply given by the far-field functions. In this case we have, from (4.50) and (4.51), that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle -\left(\overline{R}\sin \unicode[STIX]{x1D703}-{\textstyle \frac{1}{3}}\right)+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\nonumber\\ \displaystyle & & \displaystyle \text{for}~\overline{R}>0,\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle -\left(\overline{R}\sin \unicode[STIX]{x1D703}-{\textstyle \frac{1}{3}}\right)+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\nonumber\\ \displaystyle & & \displaystyle \text{for}~\overline{R}>0,\;-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0,\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
in the inner asymptotic region. In this case we observe, from (4.84) and (4.85), that each of the inner region asymptotic expansions remains uniform up to the contact point, when
$t\rightarrow 0^{+}$
in the inner asymptotic region. In this case we observe, from (4.84) and (4.85), that each of the inner region asymptotic expansions remains uniform up to the contact point, when
![]() $(\overline{X},\overline{Y})=o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
, provided that
$(\overline{X},\overline{Y})=o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2})$
, provided that
![]() $0<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/4$
. However, for
$0<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/4$
. However, for
![]() $\unicode[STIX]{x03C0}/4<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$
, a weak non-uniformity in derivatives
$\unicode[STIX]{x03C0}/4<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$
, a weak non-uniformity in derivatives
![]() $(\unicode[STIX]{x1D702}_{I,\overline{X}},\overline{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D719}_{I})$
persists close to the contact point and, in particular, when
$(\unicode[STIX]{x1D702}_{I,\overline{X}},\overline{\unicode[STIX]{x1D735}}\unicode[STIX]{x1D719}_{I})$
persists close to the contact point and, in particular, when
![]() $\overline{X}$
,
$\overline{X}$
,
![]() $\overline{Y}=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
$\overline{Y}=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
![]() $t\rightarrow 0^{+}$
. In this case, an inner–inner asymptotic region will be required when
$t\rightarrow 0^{+}$
. In this case, an inner–inner asymptotic region will be required when
![]() $\overline{X}$
,
$\overline{X}$
,
![]() $\overline{Y}=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
$\overline{Y}=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
![]() $t\rightarrow 0^{+}$
in order to correctly capture the behaviour of the free surface at the contact point.
$t\rightarrow 0^{+}$
in order to correctly capture the behaviour of the free surface at the contact point.
When
![]() $0<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/4$
, we can draw the following conclusions concerning the free surface in the inner asymptotic region.
$0<\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x03C0}/4$
, we can draw the following conclusions concerning the free surface in the inner asymptotic region.
-
(i) The contact point is located at
(4.86)as $$\begin{eqnarray}(\overline{x},y)=-{\textstyle \frac{1}{2}}t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}(\overline{x},y)=-{\textstyle \frac{1}{2}}t^{2}(-\cot \unicode[STIX]{x1D6FC},1)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
-
(ii) The free surface slope at the contact point is given by
(4.87)as $$\begin{eqnarray}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)=\unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)=\left\{\begin{array}{@{}ll@{}}o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}), & 0<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/4,\\ \displaystyle -\frac{A_{0}(\unicode[STIX]{x03C0}/4)}{\sqrt{2}}t^{2}+o(t^{2}), & \unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{\overline{x}}(\overline{X}_{p}(t),t)=\unicode[STIX]{x1D702}_{I,\overline{X}}(\overline{X}_{p}(t),t)=\left\{\begin{array}{@{}ll@{}}o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}), & 0<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/4,\\ \displaystyle -\frac{A_{0}(\unicode[STIX]{x03C0}/4)}{\sqrt{2}}t^{2}+o(t^{2}), & \unicode[STIX]{x1D6FC}=\unicode[STIX]{x03C0}/4,\end{array}\right.\end{eqnarray}$$
 $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
-
(iii) The free surface
 $\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.88)as
$\unicode[STIX]{x1D702}(\overline{X},t)$
is given by (4.88)as $$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=-\frac{1}{2}t^{2}-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x03C0}}{4\unicode[STIX]{x1D6FC}}\overline{X}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}(\overline{X},t)=-\frac{1}{2}t^{2}-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x03C0}}{4\unicode[STIX]{x1D6FC}}\overline{X}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}}),\end{eqnarray}$$
 $t\rightarrow 0^{+}$
, for
$t\rightarrow 0^{+}$
, for
 $\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.85)).
$\overline{X}\geqslant \overline{X}_{p}(t)$
(see (4.2) and (4.85)).
When
![]() $\unicode[STIX]{x03C0}/4<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$
, we consider the inner–inner asymptotic region, where
$\unicode[STIX]{x03C0}/4<\unicode[STIX]{x1D6FC}<\unicode[STIX]{x03C0}/2$
, we consider the inner–inner asymptotic region, where
![]() $(\overline{X},\overline{Y})=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
$(\overline{X},\overline{Y})=O(t^{(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC})})$
as
![]() $t\rightarrow 0^{+}$
, in the next section.
$t\rightarrow 0^{+}$
, in the next section.
5 Inner–inner region as
 $t\rightarrow 0^{+}$
when
$t\rightarrow 0^{+}$
when
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
With
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
, we set
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
, we set
![]() $(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D6E5}(t))$
, with
$(\overline{X},\overline{Y})=O(\unicode[STIX]{x1D6E5}(t))$
, with
![]() $\unicode[STIX]{x1D6E5}(t)=o(1)$
as
$\unicode[STIX]{x1D6E5}(t)=o(1)$
as
![]() $t\rightarrow 0^{+}$
in the inner–inner region. It then follows from (4.85) that
$t\rightarrow 0^{+}$
in the inner–inner region. It then follows from (4.85) that
![]() $\overline{Y}_{I}=(1/2)+\unicode[STIX]{x1D702}_{I}=O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\unicode[STIX]{x1D6E5}(t)^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
as
$\overline{Y}_{I}=(1/2)+\unicode[STIX]{x1D702}_{I}=O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}\unicode[STIX]{x1D6E5}(t)^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1})$
as
![]() $t\rightarrow 0^{+}$
in the inner–inner region. The free surface must be captured in the inner–inner region, and so we require
$t\rightarrow 0^{+}$
in the inner–inner region. The free surface must be captured in the inner–inner region, and so we require
![]() $\unicode[STIX]{x1D6E5}(t)=O(t^{\unicode[STIX]{x1D6E4}})$
, with
$\unicode[STIX]{x1D6E5}(t)=O(t^{\unicode[STIX]{x1D6E4}})$
, with
as
![]() $t\rightarrow 0^{+}$
. Thus, we introduce scaled inner–inner region coordinates
$t\rightarrow 0^{+}$
. Thus, we introduce scaled inner–inner region coordinates
![]() $(\widetilde{x},\widetilde{y})$
by the transformation
$(\widetilde{x},\widetilde{y})$
by the transformation
where
![]() $(\widetilde{x},\widetilde{y})=O(1)$
as
$(\widetilde{x},\widetilde{y})=O(1)$
as
![]() $t\rightarrow 0^{+}$
in the inner–inner region. The location of the plate in the inner–inner region is given by
$t\rightarrow 0^{+}$
in the inner–inner region. The location of the plate in the inner–inner region is given by
![]() $\widetilde{y}=-\widetilde{x}\tan \unicode[STIX]{x1D6FC}$
and the contact point is denoted by
$\widetilde{y}=-\widetilde{x}\tan \unicode[STIX]{x1D6FC}$
and the contact point is denoted by
![]() $(\widetilde{x},\widetilde{y})=(\widetilde{x}_{p}(t),\widetilde{y}_{p}(t))$
, with
$(\widetilde{x},\widetilde{y})=(\widetilde{x}_{p}(t),\widetilde{y}_{p}(t))$
, with
![]() $\overline{X}_{p}(t)=t^{\unicode[STIX]{x1D6E4}}\widetilde{x}_{p}(t)$
and
$\overline{X}_{p}(t)=t^{\unicode[STIX]{x1D6E4}}\widetilde{x}_{p}(t)$
and
![]() $\widetilde{y}_{p}(t)=-\widetilde{x}_{p}(t)\tan \unicode[STIX]{x1D6FC}$
. An examination of (4.84) and (4.85) reveals that
$\widetilde{y}_{p}(t)=-\widetilde{x}_{p}(t)\tan \unicode[STIX]{x1D6FC}$
. An examination of (4.84) and (4.85) reveals that
![]() $\unicode[STIX]{x1D702}_{I}=-1/2+O(t^{\unicode[STIX]{x1D6E4}})$
and
$\unicode[STIX]{x1D702}_{I}=-1/2+O(t^{\unicode[STIX]{x1D6E4}})$
and
![]() $\unicode[STIX]{x1D719}_{I}=1/3-t^{\unicode[STIX]{x1D6E4}}\widetilde{y}+O(t^{2\unicode[STIX]{x1D6E4}})$
as
$\unicode[STIX]{x1D719}_{I}=1/3-t^{\unicode[STIX]{x1D6E4}}\widetilde{y}+O(t^{2\unicode[STIX]{x1D6E4}})$
as
![]() $t\rightarrow 0^{+}$
in the inner–inner region. We now write the free surface and velocity potential in the inner–inner region as the expansions
$t\rightarrow 0^{+}$
in the inner–inner region. We now write the free surface and velocity potential in the inner–inner region as the expansions
where
![]() $\unicode[STIX]{x1D702}_{II}$
,
$\unicode[STIX]{x1D702}_{II}$
,
![]() $\unicode[STIX]{x1D719}_{II}=O(1)$
as
$\unicode[STIX]{x1D719}_{II}=O(1)$
as
![]() $t\rightarrow 0^{+}$
. The inner–inner region asymptotic expansions are then introduced as
$t\rightarrow 0^{+}$
. The inner–inner region asymptotic expansions are then introduced as
where
![]() $\widetilde{\unicode[STIX]{x1D702}}_{0}$
,
$\widetilde{\unicode[STIX]{x1D702}}_{0}$
,
![]() $\widetilde{\unicode[STIX]{x1D719}}_{0}=O(1)$
as
$\widetilde{\unicode[STIX]{x1D719}}_{0}=O(1)$
as
![]() $t\rightarrow 0^{+}$
. It then follows from (5.2)–(5.6) that we expand
$t\rightarrow 0^{+}$
. It then follows from (5.2)–(5.6) that we expand
![]() $\widetilde{x}_{p}(t)$
as
$\widetilde{x}_{p}(t)$
as
as
![]() $t\rightarrow 0^{+}$
. We now write [IBVP] in terms of the inner–inner region variables to obtain, at leading order, a nonlinear harmonic free boundary problem. It is convenient to introduce the following simple transformations into this problem:
$t\rightarrow 0^{+}$
. We now write [IBVP] in terms of the inner–inner region variables to obtain, at leading order, a nonlinear harmonic free boundary problem. It is convenient to introduce the following simple transformations into this problem:
where
with
The resulting boundary value problem for
![]() $\widehat{\unicode[STIX]{x1D6F7}}$
and
$\widehat{\unicode[STIX]{x1D6F7}}$
and
![]() $\widehat{H}$
is dependent only upon
$\widehat{H}$
is dependent only upon
![]() $\unicode[STIX]{x1D6FC}$
and is given by
$\unicode[STIX]{x1D6FC}$
and is given by
where
![]() $\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{y})$
and
$\widehat{\unicode[STIX]{x1D735}}=(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{x},\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\widehat{y})$
and
![]() $(\widehat{r},\unicode[STIX]{x1D703})$
are polar coordinates given by
$(\widehat{r},\unicode[STIX]{x1D703})$
are polar coordinates given by
![]() $\widehat{x}=\widehat{r}\cos \unicode[STIX]{x1D703}$
,
$\widehat{x}=\widehat{r}\cos \unicode[STIX]{x1D703}$
,
![]() $\widehat{y}=\widehat{r}\sin \unicode[STIX]{x1D703}$
. The above problem (5.11)–(5.17), hereafter termed (RBVP), is similar to that studied by Needham et al. (Reference Needham, Chamberlain and Billingham2008) for
$\widehat{y}=\widehat{r}\sin \unicode[STIX]{x1D703}$
. The above problem (5.11)–(5.17), hereafter termed (RBVP), is similar to that studied by Needham et al. (Reference Needham, Chamberlain and Billingham2008) for
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0})$
. Thus, we use the same boundary integral method to solve (RBVP) numerically and as such do not reproduce further details here. It is useful at this stage to obtain the form of quantities of interest in the inner–inner region, up to numerical constants that will be fixed by the numerical solution of (RBVP). From (5.7) and (5.8), we have
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0})$
. Thus, we use the same boundary integral method to solve (RBVP) numerically and as such do not reproduce further details here. It is useful at this stage to obtain the form of quantities of interest in the inner–inner region, up to numerical constants that will be fixed by the numerical solution of (RBVP). From (5.7) and (5.8), we have
as
![]() $t\rightarrow 0^{+}$
. From (5.2), (5.3) (5.5) and (5.8), the free surface slope at the intersection point of the free surface and the plate is given by
$t\rightarrow 0^{+}$
. From (5.2), (5.3) (5.5) and (5.8), the free surface slope at the intersection point of the free surface and the plate is given by
as
![]() $t\rightarrow 0^{+}$
. From (5.2), (5.4) (5.6) and (5.8), the fluid velocity at the contact point becomes
$t\rightarrow 0^{+}$
. From (5.2), (5.4) (5.6) and (5.8), the fluid velocity at the contact point becomes
as
![]() $t\rightarrow 0^{+}$
.
$t\rightarrow 0^{+}$
.
Numerical solutions to (RBVP) are plotted in figures 20–24. The numerical solution indicates that the free surface
![]() $\widehat{y}=\widehat{H}(\widehat{x})$
is monotone increasing in
$\widehat{y}=\widehat{H}(\widehat{x})$
is monotone increasing in
![]() $\widehat{x}\geqslant \widehat{x}_{0}$
, for all angles
$\widehat{x}\geqslant \widehat{x}_{0}$
, for all angles
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, with the gradient of the free surface at the contact point decreasing with increasing
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, with the gradient of the free surface at the contact point decreasing with increasing
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
and approaching zero as
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
and approaching zero as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2$
. In figure 20, we demonstrate the agreement of the numerical solution with the far-field asymptotic form (5.16) in (RBVP). In figure 21, we present the free surface function
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2$
. In figure 20, we demonstrate the agreement of the numerical solution with the far-field asymptotic form (5.16) in (RBVP). In figure 21, we present the free surface function
![]() $\widehat{H}(\widehat{x})$
against
$\widehat{H}(\widehat{x})$
against
![]() $\widehat{x}$
for the numerical solution of (RBVP), for a selection of angles
$\widehat{x}$
for the numerical solution of (RBVP), for a selection of angles
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Figure 23 shows plots of
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Figure 23 shows plots of
![]() $|\widehat{H}(\widehat{x}_{0})|\text{cosec}\,\unicode[STIX]{x1D6FC}$
, the distance from the origin of the
$|\widehat{H}(\widehat{x}_{0})|\text{cosec}\,\unicode[STIX]{x1D6FC}$
, the distance from the origin of the
![]() $(\widehat{x},\widehat{y})$
coordinate system to the contact point of the free surface and the plate, against
$(\widehat{x},\widehat{y})$
coordinate system to the contact point of the free surface and the plate, against
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
and figure 22 shows the numerical approximations to
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
and figure 22 shows the numerical approximations to
![]() $\widehat{x}_{0}$
,
$\widehat{x}_{0}$
,
![]() $\widehat{H}(\widehat{x}_{0})$
and
$\widehat{H}(\widehat{x}_{0})$
and
![]() $\widehat{H}_{\widehat{x}}(\widehat{x}_{0})$
against
$\widehat{H}_{\widehat{x}}(\widehat{x}_{0})$
against
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Figure 24 shows the behaviour of the free surface function very close to the plate, presented in a rotated
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Figure 24 shows the behaviour of the free surface function very close to the plate, presented in a rotated
![]() $(x,y)$
coordinate system, oriented so that the plate lies along the
$(x,y)$
coordinate system, oriented so that the plate lies along the
![]() $y$
-axis, for a typical angle
$y$
-axis, for a typical angle
![]() $\unicode[STIX]{x1D6FC}=1.56$
. The presence of very localised oscillations is revealed.
$\unicode[STIX]{x1D6FC}=1.56$
. The presence of very localised oscillations is revealed.

Figure 20. Graph of the free surface function
![]() $\widehat{H}(\widehat{x})$
against
$\widehat{H}(\widehat{x})$
against
![]() $\widehat{x}$
, showing agreement with the far-field asymptotic form (5.16), for the numerical solution of (RBVP) with
$\widehat{x}$
, showing agreement with the far-field asymptotic form (5.16), for the numerical solution of (RBVP) with
![]() $\unicode[STIX]{x1D6FC}=0.9$
, 1, 1.1, 1.2, 1.3, 1.4, 1.5 and 1.56. For each angle, a square shows
$\unicode[STIX]{x1D6FC}=0.9$
, 1, 1.1, 1.2, 1.3, 1.4, 1.5 and 1.56. For each angle, a square shows
![]() $s=250$
, after which the far-field asymptotic form (5.16) is plotted, and a dashed line shows the location of the plate.
$s=250$
, after which the far-field asymptotic form (5.16) is plotted, and a dashed line shows the location of the plate.
Figure 21. Graphs of
![]() $\widehat{H}(\widehat{x})$
against
$\widehat{H}(\widehat{x})$
against
![]() $\widehat{x}$
for the numerical solution of (RBVP). (a) Solutions with
$\widehat{x}$
for the numerical solution of (RBVP). (a) Solutions with
![]() $\unicode[STIX]{x1D6FC}=0.9$
, 1, 1.1, 1.2, 1.3, 1.4, 1.5 and 1.56; (b) solutions close to the plate with
$\unicode[STIX]{x1D6FC}=0.9$
, 1, 1.1, 1.2, 1.3, 1.4, 1.5 and 1.56; (b) solutions close to the plate with
![]() $\unicode[STIX]{x1D6FC}=1.1$
, 1.2, 1.3, 1.4, 1.5 and 1.56 for clarity. For each angle, a dashed line shows the location of the plate.
$\unicode[STIX]{x1D6FC}=1.1$
, 1.2, 1.3, 1.4, 1.5 and 1.56 for clarity. For each angle, a dashed line shows the location of the plate.
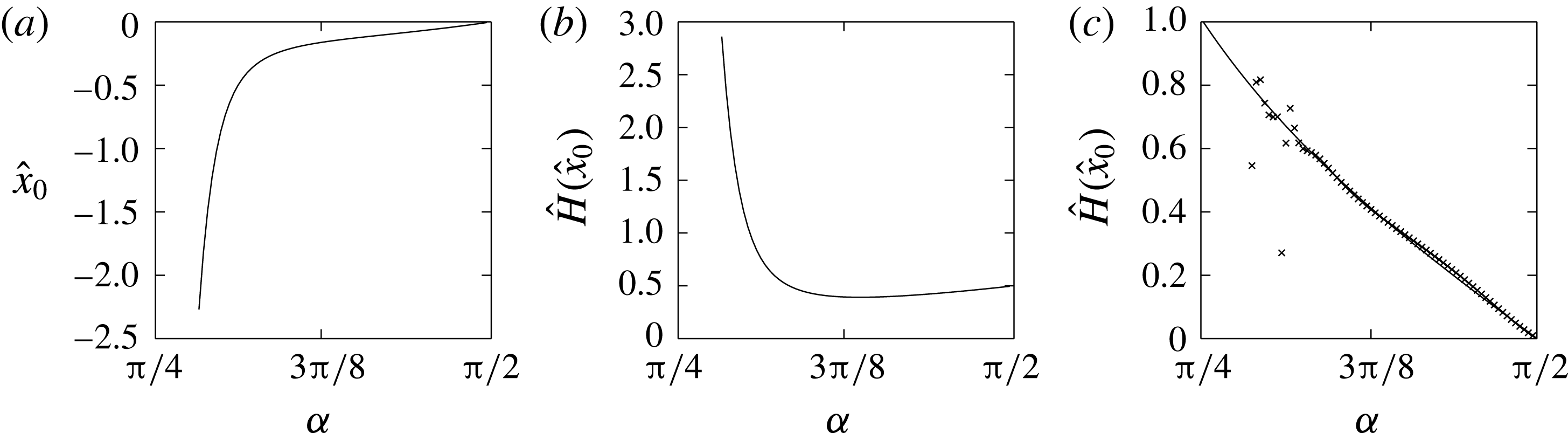
Figure 22. Numerical approximations to
![]() $\widehat{x}_{0}(\unicode[STIX]{x1D6FC})$
,
$\widehat{x}_{0}(\unicode[STIX]{x1D6FC})$
,
![]() $\widehat{H}(\widehat{x}_{0}(\unicode[STIX]{x1D6FC}))$
and
$\widehat{H}(\widehat{x}_{0}(\unicode[STIX]{x1D6FC}))$
and
![]() $\widehat{H}_{\widehat{x}}(\widehat{x}_{0}(\unicode[STIX]{x1D6FC}))$
for (RBVP). In (c), the curve
$\widehat{H}_{\widehat{x}}(\widehat{x}_{0}(\unicode[STIX]{x1D6FC}))$
for (RBVP). In (c), the curve
![]() $\tan (\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC})$
is plotted as a solid line, with numerical approximations shown as crosses.
$\tan (\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC})$
is plotted as a solid line, with numerical approximations shown as crosses.
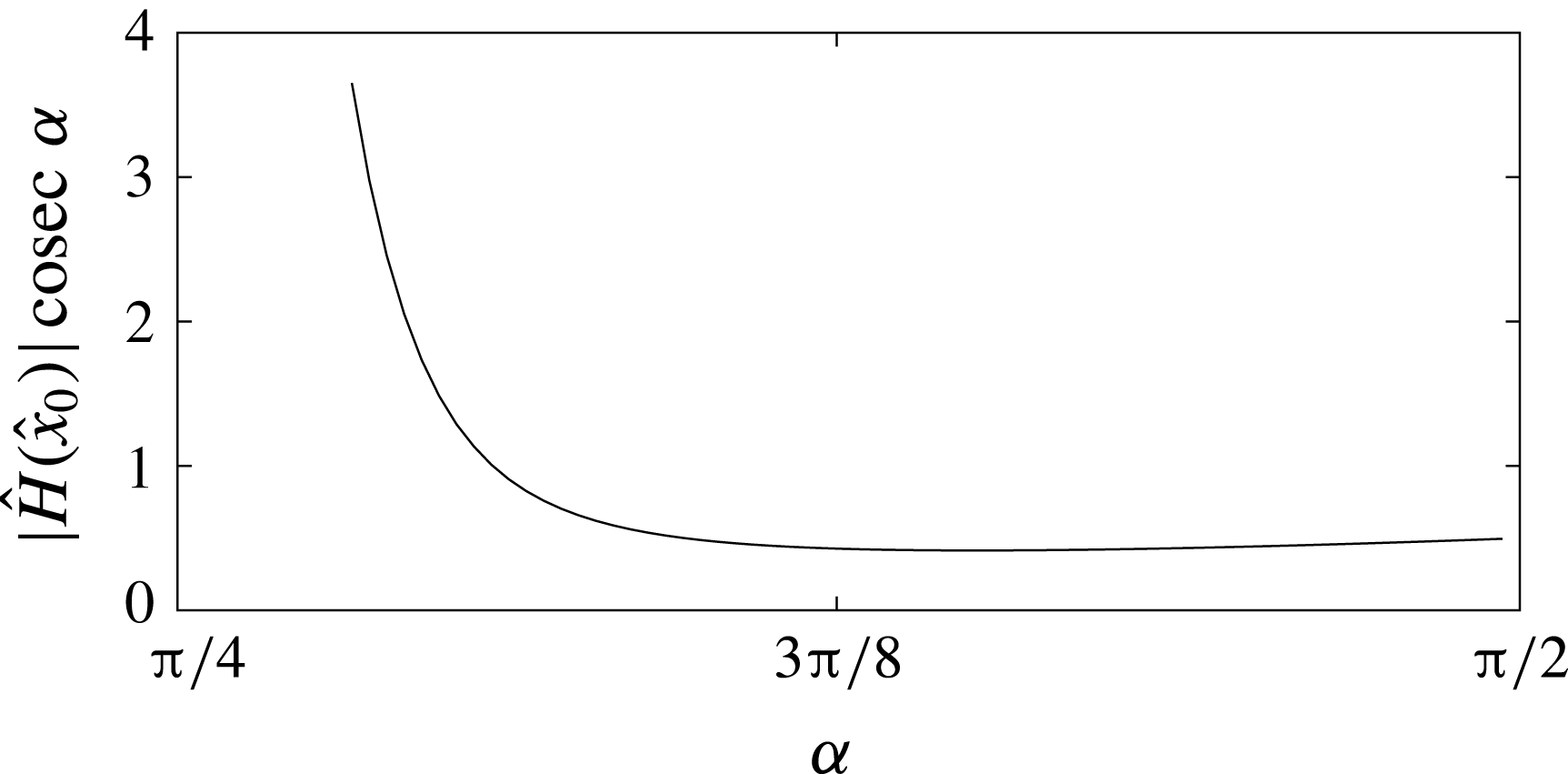
Figure 23. Graph showing the distance in the
![]() $(\widehat{x},\widehat{y})$
coordinate system from the origin of the
$(\widehat{x},\widehat{y})$
coordinate system from the origin of the
![]() $(\widehat{x},\widehat{y})$
coordinate system to the contact point of the free surface and the plate against
$(\widehat{x},\widehat{y})$
coordinate system to the contact point of the free surface and the plate against
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, as determined by the numerical solution of (RBVP).
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, as determined by the numerical solution of (RBVP).
Figure 24. The free surface close to the plate when
![]() $\unicode[STIX]{x1D6FC}=1.56$
. It should be noted that the axes have been rotated so that the plate lies along the
$\unicode[STIX]{x1D6FC}=1.56$
. It should be noted that the axes have been rotated so that the plate lies along the
![]() $y$
-axis.
$y$
-axis.
We see in figure 22(b) that
![]() $\widehat{H}(\widehat{x}_{0})$
has a minimum at
$\widehat{H}(\widehat{x}_{0})$
has a minimum at
![]() $\unicode[STIX]{x1D6FC}\approx 1.22$
, where
$\unicode[STIX]{x1D6FC}\approx 1.22$
, where
![]() $\widehat{H}(\widehat{x}_{0})\approx 0.392$
, and that
$\widehat{H}(\widehat{x}_{0})\approx 0.392$
, and that
![]() $\widehat{H}(\widehat{x}_{0})\rightarrow 1/2$
as
$\widehat{H}(\widehat{x}_{0})\rightarrow 1/2$
as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. We notice that figure 22(c) indicates that the free surface meets the plate with angle
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/2^{-}$
. We notice that figure 22(c) indicates that the free surface meets the plate with angle
![]() $\unicode[STIX]{x03C0}/2$
, for all
$\unicode[STIX]{x03C0}/2$
, for all
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. This is confirmed by the local analysis of (RBVP) in Gallagher (Reference Gallagher2015). It follows from this that the gradient of the free surface at the contact point must be given by
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. This is confirmed by the local analysis of (RBVP) in Gallagher (Reference Gallagher2015). It follows from this that the gradient of the free surface at the contact point must be given by
In figure 22(c), we plot the numerical approximation to the gradient of the free surface
![]() $\widehat{H}_{\widehat{x}}(\widehat{x}_{0})$
at the contact point against
$\widehat{H}_{\widehat{x}}(\widehat{x}_{0})$
at the contact point against
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, and compare this with
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
, and compare this with
![]() $\tan (\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC})$
. We notice the introduction of some noise into the solutions as
$\tan (\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D6FC})$
. We notice the introduction of some noise into the solutions as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/4$
; this is due to the increasing difficulty in obtaining converging solutions as
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/4$
; this is due to the increasing difficulty in obtaining converging solutions as
![]() $\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/4$
. As mentioned above, and as shown in figure 24, the numerical solution indicates that
$\unicode[STIX]{x1D6FC}\rightarrow \unicode[STIX]{x03C0}/4$
. As mentioned above, and as shown in figure 24, the numerical solution indicates that
![]() $\widehat{H}(\widehat{x})$
oscillates very rapidly very close to the contact point
$\widehat{H}(\widehat{x})$
oscillates very rapidly very close to the contact point
![]() $\widehat{x}=\widehat{x}_{0}$
. The amplitude of the oscillations is very small, decreasing to zero at the contact point, and the frequency of the oscillations increases, becoming unbounded as the contact point is approached. This local structure is entirely analogous to that reported in Needham et al. (Reference Needham, Chamberlain and Billingham2008) and can be analysed in exactly the same way. This has been performed in Gallagher (Reference Gallagher2015) and is not repeated here.
$\widehat{x}=\widehat{x}_{0}$
. The amplitude of the oscillations is very small, decreasing to zero at the contact point, and the frequency of the oscillations increases, becoming unbounded as the contact point is approached. This local structure is entirely analogous to that reported in Needham et al. (Reference Needham, Chamberlain and Billingham2008) and can be analysed in exactly the same way. This has been performed in Gallagher (Reference Gallagher2015) and is not repeated here.
Indeed, following Gallagher (Reference Gallagher2015), we can verify that the regularity conditions (2.16) are now satisfied at the contact point, and the asymptotic structure is complete. We see that the acceleration of the inclined plate induces a vertical dynamic pressure gradient of
![]() $t^{\unicode[STIX]{x1D6FE}}\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
$t^{\unicode[STIX]{x1D6FE}}\boldsymbol{j}$
, which causes the free surface, close to the intersection point of the free surface and the plate, to collapse to a height of
![]() $-t^{2}/2$
. The details in the inner–inner asymptotic region are now complete for all pairs
$-t^{2}/2$
. The details in the inner–inner asymptotic region are now complete for all pairs
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)\times \{0\}$
.
6 Conclusions
In this paper, we have studied the problem of a rigid plate, inclined at an angle
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, accelerating uniformly from rest, into or away from a semi-infinite strip of inviscid incompressible fluid, via the method of matched asymptotic expansions. We began in an outer asymptotic region in which
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
to the horizontal, accelerating uniformly from rest, into or away from a semi-infinite strip of inviscid incompressible fluid, via the method of matched asymptotic expansions. We began in an outer asymptotic region in which
![]() $(\overline{x},y)=O(1)$
as
$(\overline{x},y)=O(1)$
as
![]() $t\rightarrow 0^{+}$
. Here, we established that the leading-order terms in the outer region asymptotic expansions (3.1) for the velocity potential and the free surface elevation,
$t\rightarrow 0^{+}$
. Here, we established that the leading-order terms in the outer region asymptotic expansions (3.1) for the velocity potential and the free surface elevation,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D702}$
, satisfy the required regularity (2.16), except in a neighbourhood of the initial location of the intersection point of the free surface and the plate, at
$\unicode[STIX]{x1D702}$
, satisfy the required regularity (2.16), except in a neighbourhood of the initial location of the intersection point of the free surface and the plate, at
![]() $(\overline{x},y)=(0,0)$
. This motivated the introduction of an inner asymptotic region, in which
$(\overline{x},y)=(0,0)$
. This motivated the introduction of an inner asymptotic region, in which
![]() $(\overline{x},y)=o(1)$
as
$(\overline{x},y)=o(1)$
as
![]() $t\rightarrow 0^{+}$
, in order to capture the full regularity in this neighbourhood. It is the structure of the solution in the inner asymptotic region that reveals the interesting detail of the initial development of the flow as
$t\rightarrow 0^{+}$
, in order to capture the full regularity in this neighbourhood. It is the structure of the solution in the inner asymptotic region that reveals the interesting detail of the initial development of the flow as
![]() $t\rightarrow 0^{+}$
. We found that the structure of the solution to the problem [IBVP] in the inner region is characterised in terms of the parameters
$t\rightarrow 0^{+}$
. We found that the structure of the solution to the problem [IBVP] in the inner region is characterised in terms of the parameters
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D6FC}$
, with the results for the solution of [IBVP] in the inner asymptotic region falling into five distinct cases.
$\unicode[STIX]{x1D6FC}$
, with the results for the solution of [IBVP] in the inner asymptotic region falling into five distinct cases.
(1) The case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,\infty )$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,\unicode[STIX]{x03C0}/2)\times (0,\infty )$
Here, we solved
![]() $\text{(PBVP)}^{+}$
numerically for each
$\text{(PBVP)}^{+}$
numerically for each
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. We established that, when
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
. We established that, when
![]() $\unicode[STIX]{x1D707}>1$
, the free surface in the inner asymptotic region is monotone decreasing and rising as a local jet up the plate with height
$\unicode[STIX]{x1D707}>1$
, the free surface in the inner asymptotic region is monotone decreasing and rising as a local jet up the plate with height
![]() $(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. For
$(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. For
![]() $0<\unicode[STIX]{x1D707}<1$
, the free surface in the inner asymptotic region is monotone increasing and falling as a local plunging collapse down the plate with drop
$0<\unicode[STIX]{x1D707}<1$
, the free surface in the inner asymptotic region is monotone increasing and falling as a local plunging collapse down the plate with drop
![]() $(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. In terms of the inner region coordinates
$(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. In terms of the inner region coordinates
![]() $(\overline{X},\overline{Y})$
, it follows from (A 1) and (4.52) that on the plate in the inner region, the leading-order dynamic pressure is given by
$(\overline{X},\overline{Y})$
, it follows from (A 1) and (4.52) that on the plate in the inner region, the leading-order dynamic pressure is given by
as
![]() $t\rightarrow 0^{+}$
when
$t\rightarrow 0^{+}$
when
![]() $\overline{X}=O(1)$
. Thus, when the plate is advancing
$\overline{X}=O(1)$
. Thus, when the plate is advancing
![]() $(\unicode[STIX]{x1D707}>1)$
, the dynamic pressure on the plate increases locally to the contact point. However, when the plate is retreating
$(\unicode[STIX]{x1D707}>1)$
, the dynamic pressure on the plate increases locally to the contact point. However, when the plate is retreating
![]() $(0<\unicode[STIX]{x1D707}<1)$
, the dynamic pressure on the plate decreases locally to the contact point.
$(0<\unicode[STIX]{x1D707}<1)$
, the dynamic pressure on the plate decreases locally to the contact point.
(2) The case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{(0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}\}\times (-\infty ,0)$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{(0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}\}\times (-\infty ,0)$
Here, we solved
![]() $\text{(PBVP)}^{-}$
numerically for each
$\text{(PBVP)}^{-}$
numerically for each
![]() $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
. Pairs of near resonances occur in a small neighbourhood of
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
. Pairs of near resonances occur in a small neighbourhood of
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
). Away from the near resonance pairs, for those
$n=1,2,\ldots$
). Away from the near resonance pairs, for those
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
, the free surface has one turning point and is initially decreasing. For angles
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{1}^{\ast },\unicode[STIX]{x03C0}/2)$
, the free surface has one turning point and is initially decreasing. For angles
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{c}^{\ast },\unicode[STIX]{x1D6FC}_{1}^{\ast })$
, the free surface has two turning points and is initially increasing. For angles
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{c}^{\ast },\unicode[STIX]{x1D6FC}_{1}^{\ast })$
, the free surface has two turning points and is initially increasing. For angles
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{c}^{\ast }]$
, the free surface is monotone increasing. For angles
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x1D6FC}_{2}^{\ast },\unicode[STIX]{x1D6FC}_{c}^{\ast }]$
, the free surface is monotone increasing. For angles
![]() $(\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
$(\unicode[STIX]{x1D6FC}_{2n+1}^{\ast },\unicode[STIX]{x1D6FC}_{2n}^{\ast })$
(
![]() $n=1,2,\ldots$
), the free surface has
$n=1,2,\ldots$
), the free surface has
![]() $(2n-1)$
turning points and is initially decreasing. For angles
$(2n-1)$
turning points and is initially decreasing. For angles
![]() $(\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
$(\unicode[STIX]{x1D6FC}_{2n}^{\ast },\unicode[STIX]{x1D6FC}_{2n-1}^{\ast })$
(
![]() $n=2,3,\ldots$
), the free surface has
$n=2,3,\ldots$
), the free surface has
![]() $(2n-2)$
turning points and is initially increasing. In this case, the plate is always retreating and the free surface is falling as a local plunging collapse down the plate, with drop
$(2n-2)$
turning points and is initially increasing. In this case, the plate is always retreating and the free surface is falling as a local plunging collapse down the plate, with drop
![]() $(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. The dynamic pressure in the inner region, on the plate, is again given by (6.1) at leading order as
$(1/2)(\unicode[STIX]{x1D707}-1)t^{2}+O(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}})$
. The dynamic pressure in the inner region, on the plate, is again given by (6.1) at leading order as
![]() $t\rightarrow 0^{+}$
when
$t\rightarrow 0^{+}$
when
![]() $\overline{X}=O(1)$
. We see that the dynamic pressure on the plate decreases locally to the contact point.
$\overline{X}=O(1)$
. We see that the dynamic pressure on the plate decreases locally to the contact point.
(3) The case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}\times (-\infty ,0)$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}\times (-\infty ,0)$
Here,
![]() $\text{(PBVP)}^{-}$
has a stationary point at the intersection point of the free surface and the inclined plate. Each angle
$\text{(PBVP)}^{-}$
has a stationary point at the intersection point of the free surface and the inclined plate. Each angle
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{n}^{\ast }$
(
![]() $n=1,2,\ldots$
) separates the two near resonances in each near resonance pair. The plate is retreating and the free surface drop, and dynamic pressure on the plate, are as in case (2) above.
$n=1,2,\ldots$
) separates the two near resonances in each near resonance pair. The plate is retreating and the free surface drop, and dynamic pressure on the plate, are as in case (2) above.
(4) The case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,(1/4)\unicode[STIX]{x03C0})\times \{0\}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in (0,(1/4)\unicode[STIX]{x03C0})\times \{0\}$
In this degenerate case, the solution to the boundary value problem (4.11)–(4.14) in the inner asymptotic region is simply given by the far-field forms (4.15) and (4.16), which remain uniform up to the intersection point of the free surface and the inclined accelerating plate. The details follow those in case (1) for
![]() $0<\unicode[STIX]{x1D707}<1$
.
$0<\unicode[STIX]{x1D707}<1$
.
(5) The case
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in ((1/4)\unicode[STIX]{x03C0},(1/2)\unicode[STIX]{x03C0})\times \{0\}$
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D707})\in ((1/4)\unicode[STIX]{x03C0},(1/2)\unicode[STIX]{x03C0})\times \{0\}$
In this degenerate case, the solution to the boundary value problem (4.11)–(4.14) in the inner asymptotic region that has the least singular behaviour at the contact point is simply given by the far-field forms (4.15) and (4.16). This required the introduction of an inner–inner asymptotic region, in which
![]() $(\overline{X},\overline{Y})=o(t^{\unicode[STIX]{x1D6E4}})$
, with
$(\overline{X},\overline{Y})=o(t^{\unicode[STIX]{x1D6E4}})$
, with
![]() $\unicode[STIX]{x1D6E4}=(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/(2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC}))$
as
$\unicode[STIX]{x1D6E4}=(\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2)/(2(1-\unicode[STIX]{x03C0}/4\unicode[STIX]{x1D6FC}))$
as
![]() $t\rightarrow 0^{+}$
, in order to capture the full regularity at the contact point. Here, we solved (RBVP) numerically for each
$t\rightarrow 0^{+}$
, in order to capture the full regularity at the contact point. Here, we solved (RBVP) numerically for each
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. We established that the free surface in the inner–inner asymptotic region is monotone increasing and meets the plate with a constant angle of
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. We established that the free surface in the inner–inner asymptotic region is monotone increasing and meets the plate with a constant angle of
![]() $\unicode[STIX]{x03C0}/2$
for all
$\unicode[STIX]{x03C0}/2$
for all
![]() $\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Oscillations are present on the free surface in the inner–inner region. The overall details follow those for case (2).
$\unicode[STIX]{x1D6FC}\in (\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2)$
. Oscillations are present on the free surface in the inner–inner region. The overall details follow those for case (2).
The complex structure in the inner region, particularly when
![]() $\unicode[STIX]{x1D707}\leqslant 0$
, leads us to pose the following two related questions. Is the problem [IBVP] well-posed with respect to perturbations in initial data in the inner asymptotic region? When the problem [IBVP] is well-posed, is it stable with respect to perturbations in initial data in the inner asymptotic region? We shall consider these two questions in detail in the companion paper Gallagher et al. (Reference Gallagher, Needham and Billingham2018). In anticipation of the analysis in this companion paper, we make the following observations relating to the present results, and, in particular, relating to the emergence of a more complex structure in
$\unicode[STIX]{x1D707}\leqslant 0$
, leads us to pose the following two related questions. Is the problem [IBVP] well-posed with respect to perturbations in initial data in the inner asymptotic region? When the problem [IBVP] is well-posed, is it stable with respect to perturbations in initial data in the inner asymptotic region? We shall consider these two questions in detail in the companion paper Gallagher et al. (Reference Gallagher, Needham and Billingham2018). In anticipation of the analysis in this companion paper, we make the following observations relating to the present results, and, in particular, relating to the emergence of a more complex structure in
![]() $\unicode[STIX]{x1D707}\leqslant 0$
than that when
$\unicode[STIX]{x1D707}\leqslant 0$
than that when
![]() $\unicode[STIX]{x1D707}>0$
: from a physical point of view, when
$\unicode[STIX]{x1D707}>0$
: from a physical point of view, when
![]() $\unicode[STIX]{x1D707}<1$
, then cases (1)–(5) reveal that in the inner (or inner–inner) region, at leading order, the free surface plunges downwards locally with dimensionless acceleration
$\unicode[STIX]{x1D707}<1$
, then cases (1)–(5) reveal that in the inner (or inner–inner) region, at leading order, the free surface plunges downwards locally with dimensionless acceleration
![]() $(\unicode[STIX]{x1D707}-1)$
; when this acceleration is less than that due to gravity (unity in dimensionless variables), then
$(\unicode[STIX]{x1D707}-1)$
; when this acceleration is less than that due to gravity (unity in dimensionless variables), then
![]() $\unicode[STIX]{x1D707}>0$
, while when this acceleration exceeds that due to gravity, then
$\unicode[STIX]{x1D707}>0$
, while when this acceleration exceeds that due to gravity, then
![]() $\unicode[STIX]{x1D707}<0$
; this indicates that well-posedness and temporal stability may be expected when
$\unicode[STIX]{x1D707}<0$
; this indicates that well-posedness and temporal stability may be expected when
![]() $\unicode[STIX]{x1D707}>0$
, while a rapidly developing instability, and even ill-posedness, may be expected close to the contact point when
$\unicode[STIX]{x1D707}>0$
, while a rapidly developing instability, and even ill-posedness, may be expected close to the contact point when
![]() $\unicode[STIX]{x1D707}<0$
. Indeed, experimental work on this problem by S. Thoroddsen, which remains unpublished, has indicated that the initial flow close to the contact point is regular and well-resolved when
$\unicode[STIX]{x1D707}<0$
. Indeed, experimental work on this problem by S. Thoroddsen, which remains unpublished, has indicated that the initial flow close to the contact point is regular and well-resolved when
![]() $\unicode[STIX]{x1D707}>0$
, but becomes very rapidly complex and finely structured when
$\unicode[STIX]{x1D707}>0$
, but becomes very rapidly complex and finely structured when
![]() $\unicode[STIX]{x1D707}<0$
, which gives support to this conjecture, and, in particular, to the conclusions of the companion paper.
$\unicode[STIX]{x1D707}<0$
, which gives support to this conjecture, and, in particular, to the conclusions of the companion paper.
Acknowledgements
M.T.G. gratefully acknowledges financial support from EPSRC Grant EP/H007830/1. We would like to thank all of the referees for their detailed reading of the paper. Their comments have enabled us to significantly improve the paper.
Appendix A. Reconstructing the dynamic pressure and fluid velocity fields in the inner region
A.1 The case
 $\unicode[STIX]{x1D707}>0$
with
$\unicode[STIX]{x1D707}>0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
An examination of (2.15) and (4.2) requires that we write in the inner asymptotic region
after which we have, from (2.15), (4.2) and (4.57), the inner region asymptotic expansion for the dynamic fluid pressure field as
 $$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.57), as
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.57), as
 $$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719} & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\boldsymbol{j}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t)=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719} & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D707}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{+}\left(\frac{\overline{X}}{\unicode[STIX]{x1D707}},\frac{\overline{Y}}{\unicode[STIX]{x1D707}}\right)\boldsymbol{j}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
A.2 The case
 $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)\backslash \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
The inner region asymptotic expansion for the dynamic fluid pressure field is given, from (2.15), (4.2), (A 1) and (4.69), as
 $$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.69), as
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.69), as
 $$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t) & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{j}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t) & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}A_{0}(\unicode[STIX]{x1D6FC})(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC},\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{j}\right)+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
$-\overline{X}\tan \unicode[STIX]{x1D6FC}\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
A.3 The case
 $\unicode[STIX]{x1D707}<0$
with
$\unicode[STIX]{x1D707}<0$
with
 $\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
$\unicode[STIX]{x1D6FC}\in \{\unicode[STIX]{x1D6FC}_{n}^{\ast }:n=1,2,\ldots \,\}$
The inner region asymptotic expansion for the dynamic fluid pressure field is given, from (2.15), (4.2), (A 1) and (4.69), as
 $$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}_{n}^{\ast }}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{I}(\overline{X},\overline{Y},t) & = & \displaystyle \frac{1}{2}(\unicode[STIX]{x1D707}-1)(1-2\overline{Y})\nonumber\\ \displaystyle & & \displaystyle +\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }}\left(2\overline{X}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right.\nonumber\\ \displaystyle & & \displaystyle +\left.2\overline{Y}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)-\left(1+\frac{\unicode[STIX]{x03C0}}{\unicode[STIX]{x1D6FC}_{n}^{\ast }}\right)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast }}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast }\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.69), as
$-\overline{X}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast }\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
. In the inner region, the fluid velocity field is given, from (4.2) and (4.69), as
 $$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t) & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }}\nonumber\\ \displaystyle & & \displaystyle \times \left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{i}+\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{j}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{X},\overline{Y},t) & = & \displaystyle t(\unicode[STIX]{x1D707}-1)\boldsymbol{j}+t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-1}A_{0}(\unicode[STIX]{x1D6FC}_{n}^{\ast })(\unicode[STIX]{x1D707}-1)\cos \unicode[STIX]{x1D6FC}_{n}^{\ast }(-\unicode[STIX]{x1D707})^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}_{n}^{\ast }}\nonumber\\ \displaystyle & & \displaystyle \times \left(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{X}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{i}+\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}_{n}^{\ast },\overline{Y}}^{-}\left(\frac{\overline{X}}{(-\unicode[STIX]{x1D707})},\frac{\overline{Y}}{(-\unicode[STIX]{x1D707})}\right)\boldsymbol{j}\right)\nonumber\\ \displaystyle & & \displaystyle +\,o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}_{n}^{\ast }-2}),\end{eqnarray}$$
as
![]() $t\rightarrow 0^{+}$
, with
$t\rightarrow 0^{+}$
, with
![]() $\overline{X}\geqslant \overline{X}_{p}(t)$
,
$\overline{X}\geqslant \overline{X}_{p}(t)$
,
![]() $-\overline{X}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast }\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
$-\overline{X}\tan \unicode[STIX]{x1D6FC}_{n}^{\ast }\leqslant \overline{Y}\leqslant \overline{Y}_{I}(\overline{X},t)$
.
A.4 The case
 $\unicode[STIX]{x1D707}=0$
with
$\unicode[STIX]{x1D707}=0$
with
 $\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
$\unicode[STIX]{x1D6FC}\in (0,\unicode[STIX]{x03C0}/2)$
The inner region asymptotic expansion for the dynamic fluid pressure field is given, from (2.15), (4.2), (A 1) and (4.84), as
 $$\begin{eqnarray}\displaystyle p_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle \left(\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{2}\right)\nonumber\\ \displaystyle & & \displaystyle -\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p_{I}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle \left(\overline{R}\sin \unicode[STIX]{x1D703}-\frac{1}{2}\right)\nonumber\\ \displaystyle & & \displaystyle -\,t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}}\cos \frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC})+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-2}),\end{eqnarray}$$
for
![]() $\overline{R}>0$
, with
$\overline{R}>0$
, with
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, as
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, as
![]() $t\rightarrow 0^{+}$
in the inner region. In the inner region, the fluid velocity field is given, from (4.2) and (4.84), as
$t\rightarrow 0^{+}$
in the inner region. In the inner region, the fluid velocity field is given, from (4.2) and (4.84), as
 $$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle -t\boldsymbol{j}-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\left(\sin \left(1-\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D703}\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\cos \left(1-\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D703}\boldsymbol{j}\right)(1+O(\overline{R}))+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{q}(\overline{R},\unicode[STIX]{x1D703},t) & = & \displaystyle -t\boldsymbol{j}-t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}-1}\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}A_{0}(\unicode[STIX]{x1D6FC})\cos \unicode[STIX]{x1D6FC}\overline{R}^{\unicode[STIX]{x03C0}/2\unicode[STIX]{x1D6FC}-1}\left(\sin \left(1-\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D703}\boldsymbol{i}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\cos \left(1-\frac{\unicode[STIX]{x03C0}}{2\unicode[STIX]{x1D6FC}}\right)\unicode[STIX]{x1D703}\boldsymbol{j}\right)(1+O(\overline{R}))+o(t^{\unicode[STIX]{x03C0}/\unicode[STIX]{x1D6FC}+1}),\end{eqnarray}$$
for
![]() $\overline{R}>0$
, with
$\overline{R}>0$
, with
![]() $-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, as
$-\unicode[STIX]{x1D6FC}\leqslant \unicode[STIX]{x1D703}\leqslant 0$
, as
![]() $t\rightarrow 0^{+}$
in the inner region.
$t\rightarrow 0^{+}$
in the inner region.