Published online by Cambridge University Press: 28 April 2011
We calculate the rheological properties of a dilute emulsion of neutrally buoyant nearly spherical drops at O(φRe3/2) in a simple shear flow(u∞ = 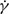 x211,
x211, 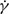 being the shear rate) as a function of the ratio of the dispersed- and continuous-phase viscosities (λ =
being the shear rate) as a function of the ratio of the dispersed- and continuous-phase viscosities (λ = 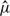 /μ). Here, φ is the volume fraction of the dispersed phase and Re is the micro-scale Reynolds number. The latter parameter is a dimensionless measure of inertial effects on the scale of the dispersed-phase constituents and is defined as Re =
/μ). Here, φ is the volume fraction of the dispersed phase and Re is the micro-scale Reynolds number. The latter parameter is a dimensionless measure of inertial effects on the scale of the dispersed-phase constituents and is defined as Re = 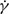 a2ρ/μ, a being the drop radius and ρ the common density of the two phases. The analysis is restricted to the limit φ, Re ≪ 1, when hydrodynamic interactions between drops may be neglected, and the velocity field in a region around the drop of the order of its own size is governed by the Stokes equations at leading order. The dominant contribution to the rheology at O(φRe3/2), however, arises from the so-called outer region where the leading-order Stokes approximation ceases to be valid. The relevant length scale in this outer region, the inertial screening length, results from a balance of convection and viscous diffusion, and is O(aRe−1/2) for simple shear flow in the limit Re ≪ 1. The neutrally buoyant drop appears as a point-force dipole on this scale. The rheological calculation at O(φRe3/2) is therefore based on a solution of the linearized Navier–Stokes equations forced by a point dipole. The principal contributions to the bulk rheological properties at this order arise from inertial corrections to the drop stresslet and Reynolds stress integrals. The theoretical calculations for the stresslet components are validated via finite volume simulations of a spherical drop at finite Re; the latter extend up to Re ≈ 10.
a2ρ/μ, a being the drop radius and ρ the common density of the two phases. The analysis is restricted to the limit φ, Re ≪ 1, when hydrodynamic interactions between drops may be neglected, and the velocity field in a region around the drop of the order of its own size is governed by the Stokes equations at leading order. The dominant contribution to the rheology at O(φRe3/2), however, arises from the so-called outer region where the leading-order Stokes approximation ceases to be valid. The relevant length scale in this outer region, the inertial screening length, results from a balance of convection and viscous diffusion, and is O(aRe−1/2) for simple shear flow in the limit Re ≪ 1. The neutrally buoyant drop appears as a point-force dipole on this scale. The rheological calculation at O(φRe3/2) is therefore based on a solution of the linearized Navier–Stokes equations forced by a point dipole. The principal contributions to the bulk rheological properties at this order arise from inertial corrections to the drop stresslet and Reynolds stress integrals. The theoretical calculations for the stresslet components are validated via finite volume simulations of a spherical drop at finite Re; the latter extend up to Re ≈ 10.
Combining the results of our O(φRe3/2) analysis with the known rheology of a dilute emulsion to O(φRe) leads to the following expressions for the relative viscosity (μe), and the non-dimensional first (N1) and second normal stress differences (N2) to O(φRe3/2): μe = 1 + φ[(5λ+2)/(2(λ+1))+0.024Re3/2(5λ+2)2/(λ+1)2]; N1=φ[−Re4(3λ2+3λ+1)/(9(λ+1)2)+0.066Re3/2(5λ+2)2/(λ+1)2] and N2 = φ[Re2(105λ2+96λ+35)/(315(λ+1)2)−0.085Re3/2(5λ+2)2/(λ+1)2].
Thus, for small but finite Re, inertia endows an emulsion with a non-Newtonian rheology even in the infinitely dilute limit, and in particular, our calculations show that, aside from normal stress differences, such an emulsion also exhibits a shear-thickening behaviour. The results for a suspension of rigid spherical particles are obtained in the limit λ → ∞.