Hostname: page-component-5cf477f64f-tx7qf Total loading time: 0 Render date: 2025-04-05T08:22:55.540Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of shear-dependent rheology on turbulent pipe flow

Published online by Cambridge University Press:  08 June 2017

J. Singh Open the ORCID record for J. Singh [Opens in a new window] ,
M. Rudman  and
H. M. Blackburn
J. Singh
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
M. Rudman*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

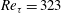Direct numerical simulations of turbulent pipe flow of power-law fluids at $Re_{\unicode[STIX]{x1D70F}}=323$ are analysed in order to understand the way in which shear thinning or thickening affects first- and second-order flow statistics including turbulent kinetic energy production, transport and dissipation in such flows. The results show that with shear thinning, near-wall streaks become weaker and the axial and azimuthal correlation lengths of axial velocity fluctuations increase. Viscosity fluctuations give rise to an additional shear stress term in the mean momentum equation which is negative for shear-thinning fluids and which increases in magnitude as the fluid becomes more shear thinning: for an equal mean wall shear stress, this term increases the mean velocity gradient in shear-thinning fluids when compared to a Newtonian fluid. Consequently, the mean velocity profile in power-law fluids deviates from the law of the wall 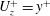$U_{z}^{+}=y^{+}$ in the viscous sublayer when traditional near-wall scaling is used. Consideration is briefly given to an alternative scaling that allows the law of wall to be recovered but which results in loss of a common mean stress profile. With shear thinning, the mean viscosity increases slightly at the wall and its profile appears to be approximately logarithmic in the velocity log layer. Through analysis of the turbulent kinetic energy budget, undertaken here for the first time for generalised Newtonian fluids, it is shown that shear thinning decreases the overall turbulent kinetic energy production but widens the wall-normal region where it is generated. Additional dissipation terms in the mean flow and turbulent kinetic energy budget equations arise from viscosity fluctuations; with shear thinning, these result in a net decrease in the total viscous dissipation. The overall effect of shear thinning on the turbulent kinetic energy budget is found to be largely confined to the inner layers, 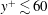$y^{+}\lesssim 60$.

JFM classification

Non-Newtonian Flows: Non-Newtonian Flows Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 822 , 10 July 2017 , pp. 848 - 879
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackburn, H. M. & Sherwin, S. J. 2004 Formulation of a Galerkin spectral element–Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Chhabra, R. P. & Richardson, J. F. 2008 Non-Newtonian Flow and Applied Rheology, 2nd edn. Elsevier.Google Scholar
Chilton, R. & Stainsby, R. 1998 Pressure loss equations for laminar and turbulent non-Newtonian pipe flow. J. Hydraul. Engng ASCE 124 (5), 522–529.Google Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014 Reynolds number effects in dns of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.Google Scholar
Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22 (11), 115107.Google Scholar
Clapp, R. M. 1961 Turbulent heat transfer in pseudoplastic non-Newtonian fluids. Intl Developments in Heat Transfer, ASME, Part III, Sec. A 652–661.Google Scholar
Cruz, D. O. A. & Pinho, F. T. 2003 Turbulent pipe flow predictions with a low Reynolds number k-𝜀 model for drag reducing fluids. J. Non-Newtonian Fluid Mech. 114 (2), 109–148.CrossRefGoogle Scholar
Dodge, D. W. & Metzner, A. B. 1959 Turbulent flow of non-Newtonian systems. AIChE J. 5, 189–204.Google Scholar
Eggels, J. G., Unger, F., Wiess, M. H., Westerweel, J., Adrian, R. J., Friedrich, R. & Nieuwstadt, F. T. M. 1994 Fully developed turbulent pipe flow: a comparison between direct numerical simulation and experiment. J. Fluid Mech. 268, 175–209.Google Scholar
Gavrilov, A. A. & Rudyak, V. Ya. 2016 Direct numerical simulation of the turbulent flows of power-law fluids in a circular pipe. Thermophys. Aeromech. 23 (4), 473–486.Google Scholar
Gnambode, P. S., Orlandi, P., Ould-Rouiss, M. & Nicolas, X. 2015 Large-eddy simulation of turbulent pipe flow of power-law fluids. Intl J. Heat Fluid Flow 54, 196–210.Google Scholar
Guermond, J. L., Minev, P. & Shen, J. 2006 An overview of projection methods for incompressible flows. Comput. Meth. Appl. Mech. Engng 195, 6011–6045.Google Scholar
Guzel, B., Frigaard, I. & Martinez, D. M. 2009 Predicting laminar turbulent transition in Poiseuille pipe flow for non-Newtonian fluids. Chem. Engng Sci. 64 (2), 254–264.CrossRefGoogle Scholar
Hartnett, J. P. & Kostic, M. 1990 Turbulent friction factor correlations for power law fluids in circular and non-circular channels. Intl Commun. Heat Mass Transfer 17 (1), 59–65.Google Scholar
Hutchins, N & Marusic, Ivan 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
Leslie, D. C. & Gao, S. 1988 The stability of spectral schemes for the large eddy simulation of channel flows. Intl J. Numer. Meth. Fluids 8 (9), 1107–1116.Google Scholar
Madlener, K., Frey, B. & Ciezki, H. K. 2009 Generalized Reynolds number for non-Newtonian fluids. Progr. Propul. Phys. 1, 237–250.CrossRefGoogle Scholar
Malin, M. R. 1997 Turbulent pipe flow of power-law fluids. Intl Commun. Heat Mass Transfer 24, 977–988.Google Scholar
Metzner, A. B. & Reed, J. C. 1955 Flow of non-Newtonian fluids – correlations for laminar, transition and turbulent flow regimes. AIChE J. 1, 434–444.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Ohta, T. & Miyashita, M. 2014 DNS and LES with an extended Smagorinsky model for wall turbulence in non-Newtonian viscous fluids. J. Non-Newtonian Fluid Mech. 206, 29–39.CrossRefGoogle Scholar
Pinho, F. T. 2003 A GNF framework for turbulent flow models of drag-reducing fluids and a proposal for a k–𝜀 type closure. J. Non-Newtonian Fluid Mech. 114, 149–184.Google Scholar
Pinho, F. T. & Whitelaw, J. H. 1990 Flow of non-Newtonian fluids in a pipe. J. Non-Newtonian Fluid Mech. 34, 129–144.Google Scholar
Piomelli, U. 1997 Large-eddy simulations: where we stand. In Advances in DNS/LES (ed. Liu, C. & Liu, Z.), pp. 93–104. AFOSR.Google Scholar
Pope, S. B 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Ptasinski, P. K., Boersma, B. J., Nieuwstadt, F. T. M., Hulsen, M. A., Van den Brule, B. H. A. A. & Hunt, J. C. R. 2003 Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms. J. Fluid Mech. 490, 251–291.Google Scholar
Ptasinski, P. K., Nieuwstadt, F. T. M., Van den Brule, B. H. A. A. & Hulsen, M. A. 2001 Experiments in turbulent pipe flow with polymer additives at maximum drag reduction. Flow Turbul. Combust. 66, 159–182.Google Scholar
Rudman, M. & Blackburn, H. M. 2006 Direct numerical simulation of turbulent non-Newtonian flow using a spectral element method. Appl. Math. Model 30, 1229–1248.Google Scholar
Rudman, M., Blackburn, H. M., Graham, L. J. W. & Pullum, L. 2004 Turbulent pipe flow of non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 118 (1), 33–48.CrossRefGoogle Scholar
Rudman, M., Graham, L. J. W., Blackburn, H. M. & Pullum, L. 2002 Non-Newtonian turbulent and transitional pipe flow. In 15th Int. Conf. Hydrotransport, pp. 271–286. BHR Group.Google Scholar
Singh, J., Rudman, M., Blackburn, H. M., Chryss, A., Pullum, L. & Grahah, L. J. W. 2016 The importance of rheology characterization in predicting turbulent pipe flow of generalized Newtonian fluids. J. Non-Newtonian Fluid Mech. 232, 11–21.Google Scholar
Slatter, P. T. & Lazarus, J. H. 1993 Critical flow in slurry pipeline. In 12th Int. Conf. on Slurry Handling and Pipeline Transport, Hydrotransport 12, pp. 639–658. BHRG Fluid Engineering, Cranfield.Google Scholar
Thais, L., Gatski, T. B. & Mompean, G. 2013 Analysis of polymer drag reduction mechanisms from energy budgets. Intl J. Heat Fluid Flow 43, 52–61.Google Scholar
Tomita, Y. 1959 A study of non-Newtonian flow in pipe lines. Bull. JSME 2 (5), 10–16.Google Scholar
den Toonder, J. M. J. & Nieuwstadt, F. T. M. 1997 Reynolds number effects in a turbulent pipe flow for low to moderate Re . Phys. Fluids 9 (11), 3398–3409.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48 (1), 131–158.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (01), 39–48.Google Scholar
Wilson, K. C. & Thomas, A. D. 1985 A new analysis of the turbulent flow of non-Newtonian fluids. Can. J. Chem. Engng 63, 539–546.CrossRefGoogle Scholar