Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-24T17:25:37.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of lock aspect ratio upon the evolution of an axisymmetric intrusion

Published online by Cambridge University Press:  21 October 2013

Amber M. Holdsworth  and
Bruce R. Sutherland
Amber M. Holdsworth
Affiliation:
Departments of Physics and of Earth & Atmospheric Sciences, University of Alberta, Edmonton, AB, Canada T6G 2E1
Bruce R. Sutherland*
Affiliation:
Departments of Physics and of Earth & Atmospheric Sciences, University of Alberta, Edmonton, AB, Canada T6G 2E1
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Through theory and numerical simulations in an axisymmetric geometry, we examine evolution of a symmetric intrusion released from a cylindrical lock in stratified fluid as it depends upon the ambient interface thickness, 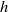$h$, and the lock aspect ratio 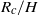${R}_{c} / H$, in which ${R}_{c} $ is the lock radius and 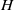$H$ is the ambient depth. Whereas self-similarity and shallow-water theory predicts that intrusions, once established, should decelerate shortly after release from the lock, we find that the intrusions rapidly accelerate and then enter a constant-speed regime that extend between 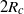$2{R}_{c} $ and 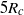$5{R}_{c} $ from the gate, depending upon the relative interface thickness 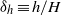${\delta }_{h} \equiv h/ H$. This result is consistent with previously performed laboratory experiments. Scaling arguments predict that the distance, 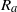${R}_{a} $, over which the lock fluid first accelerates increases linearly with 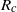${R}_{c} $ if 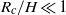${R}_{c} / H\ll 1$ and 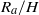${R}_{a} / H$ approaches a constant for high aspect ratios. Likewise in the constant-speed regime, the speed relative to the rectilinear speed, 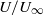$U/ {U}_{\infty } $, increases linearly with 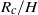${R}_{c} / H$ if the aspect ratio is small and is of order unity if 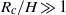${R}_{c} / H\gg 1$. Beyond the constant-speed regime, the intrusion front decelerates rapidly, with power-law exponent as large as 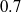$0. 7$ if the relative ambient interface thickness, 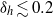${\delta }_{h} \lesssim 0. 2$. For intrusions in uniformly stratified fluid (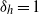${\delta }_{h} = 1$), the power-law exponent is close to 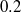$0. 2$. Except in special cases, the exponents differ significantly from the 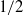$1/ 2$ power predicted from self-similarity and the $1/ 3$ power predicted for intrusions from partial-depth lock releases.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 735 , 25 November 2013 , R3
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. & Sparks, R. S. J. 2005 Dynamics of giant volcanic ash clouds from supervolcanic eruptions. Geophys. Rev. Lett. 32, L24808.CrossRefGoogle Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Bolster, D., Hang, A. & Linden, P. F. 2008 The front speed of intrusions into a continuously stratified medium. J. Fluid Mech. 594, 369–377.CrossRefGoogle Scholar
Cheong, H., Kuenen, J. J. P. & Linden, P. F. 2006 The front speed of intrusive gravity currents. J. Fluid Mech. 552, 1–11.CrossRefGoogle Scholar
Flynn, M. R. & Linden, P. F. 2006 Intrusive gravity currents. J. Fluid Mech. 568, 193–202.CrossRefGoogle Scholar
Flynn, M. R. & Sutherland, B. R. 2004 Intrusive gravity currents and internal wave generation in stratified fluid. J. Fluid Mech. 514, 355–383.CrossRefGoogle Scholar
Hallworth, M. A., Huppert, H. E. & Ungarish, M. 2001 Axisymmetric gravity currents in a rotating system: experimental and numerical investigations. J. Fluid Mech. 447, 1–29.CrossRefGoogle Scholar
Holdsworth, A. M., Barrett, K. J. & Sutherland, B. R. 2012 Axisymmetric intrusions in two-layer and uniformly stratified environments with and without rotation. Phys. Fluids 24, 036603.CrossRefGoogle Scholar
Holyer, J. Y. & Huppert, H. E. 1980 Gravity currents entering a two-layer fluid. J. Fluid Mech. 100, 739–767.CrossRefGoogle Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.CrossRefGoogle Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.CrossRefGoogle Scholar
Maxworthy, T., Leilich, J., Simpson, J. & Meiburg, E. H. 2002 The propagation of a gravity current in a linearly stratified fluid. J. Fluid Mech. 453, 371–394.CrossRefGoogle Scholar
McMillan, J. M. & Sutherland, B. R. 2010 The lifecycle of axisymmetric internal solitary waves. Nonlinear Process. Geophys. 17, 443–453.CrossRefGoogle Scholar
Munroe, J. R., Voegeli, C., Sutherland, B. R., Birman, V. & Meiburg, E. H. 2009 Intrusive gravity currents from finite-length locks in a uniformly stratified fluid. J. Fluid Mech. 635, 245–273.CrossRefGoogle Scholar
Nash, J. D. & Moum, J. N. 2005 River plumes as a source of large-amplitude internal waves in the coastal ocean. Nature 437, 400–403.CrossRefGoogle ScholarPubMed
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Shin, J., Dalziel, S. & Linden, P. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Sutherland, B. R., Chow, A. N. F. & Pittman, T. P. 2007 The collapse of a mixed patch in stratified fluid. Phys. Fluids 19, 116602.CrossRefGoogle Scholar
Sutherland, B. R. & Nault, J. T. 2007 Intrusive gravity currents propagating along thin and thick interfaces. J. Fluid Mech. 586, 109–118.CrossRefGoogle Scholar
Ungarish, M. 2005 Intrusive gravity currents in a stratified ambient: shallow-water theory and numerical results. J. Fluid Mech. 535, 287–323.CrossRefGoogle Scholar
Ungarish, M. 2006 On gravity currents in a linearly stratified ambient: a generalization of Benjamin’s steady-state propagation results. J. Fluid Mech. 548, 49–68.CrossRefGoogle Scholar
Ungarish, M. & Zemach, T. 2007 On axisymmetric gravity currents in a stratified ambient – shallow-water theory and numerical results. Eur. J. Mech. (B/Fluids) 26, 220–235.CrossRefGoogle Scholar
Wu, J. 1969 Mixed region collapse with internal wave generation in a density stratified medium. J. Fluid Mech. 35, 531–544.CrossRefGoogle Scholar
Zemach, T. & Ungarish, M. 2007 On axisymmetric intrusive gravity currents: the approach to self-similarity solutions of the shallow-water equations in a linearly stratified ambient. Proc. R. Soc.Lond. A 463, 2085–2165.Google Scholar