Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T23:33:28.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of large-scale accelerating motions on turbulent pipe and channel flows

Published online by Cambridge University Press:  09 September 2016

Jinyul Hwang ,
Jin Lee  and
Hyung Jin Sung
Jinyul Hwang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
Jin Lee
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation data from turbulent pipe and channel flows at $\mathit{Re}_{\unicode[STIX]{x1D70F}}\approx 930$ are used to investigate their statistical difference by focusing on large-scale motions (LSMs). The contribution to the bulk production of turbulent kinetic energy shows marked differences in the overlap and core regions. These discrepancies arise from the dominant contributions of the LSMs (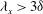$\unicode[STIX]{x1D706}_{x}>3\unicode[STIX]{x1D6FF}$) to the Reynolds shear stress in the channel flow. The spectrum of the net Reynolds shear force reveals that the LSMs accelerate the mean flow in the overlap region. The net force spectrum is further decomposed into the spectra of velocity–vorticity correlations, 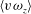$\langle v\unicode[STIX]{x1D714}_{z}\rangle$ and 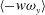$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$, which are related to the advective vorticity transport and the change-of-scale effect, respectively. The dominance of large-scale accelerating motions (LSAMs) in the overlap region of the channel flow is due to the contribution of 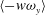$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ at longer wavelengths ($\unicode[STIX]{x1D706}_{x}>3\unicode[STIX]{x1D6FF}$), The LSAMs are related to the long low-speed regions, and these regions are longer and wider in the channel flow than in the pipe flow. Due to the pipe curvature, the spanwise size of the LSMs is restricted by neighbouring LSMs and the spanwise velocity fluctuations are reduced. The contribution of 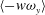$\langle -w\unicode[STIX]{x1D714}_{y}\rangle$ to the acceleration is prominent in the channel flow, leading to the dominance of the LSAMs associated with the change-of-scale effect.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 420 - 441
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.CrossRefGoogle Scholar
Afzal, N. 1982 Fully developed turbulent flow in a pipe: an intermediate layer. Ing-Arch. 52, 355–377.Google Scholar
Ahn, J., Lee, J. H., Jang, S. J. & Sung, H. J. 2013 Direct numerical simulations of fully developed turbulent pipe flows for Re 𝜏 = 180, 544 and 934. Intl J. Heat Fluid Flow 44, 222–228.CrossRefGoogle Scholar
Ahn, J., Lee, J. H., Lee, J., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27 (6), 065110.CrossRefGoogle Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google ScholarPubMed
Bailey, S. C. C. & Smits, A. J. 2010 Experimental investigation of structure of large- and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 651, 339–356.Google Scholar
Buschmann, M. H. & Gad-el Hak, M. 2010 Normal and cross-flow Reynolds stresses: differences between confined and semi-confined flows. Exp. Fluids 49 (1), 213–223.Google Scholar
Chin, C., Monty, J. P. & Ooi, A. 2014a Reynolds number effects in DNS of pipe flow and comparison with channels and boundary layers. Intl J. Heat Fluid Flow 45, 33–40.CrossRefGoogle Scholar
Chin, C., Philip, J., Klewicki, J., Ooi, A. & Marusic, I. 2014b Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows. J. Fluid Mech. 757, 747–769.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Chung, D., Marusic, I., Monty, J. P., Vallikivi, M. & Smits, A. J. 2015 On the universality of inertial energy in the log layer of turbulent boundary layer and pipe flows. Exp. Fluids 56 (7), 1–10.Google Scholar
El Khoury, G. K., Schlatter, P., Brethouwer, G. & Johansson, A. V. 2014 Turbulent pipe flow: statistics, Re-dependence, structures and similarities with channel and boundary layer flows. J. Phys.: Conf. Ser. 506, 012010.Google Scholar
Ganapathisubramani, B. 2008 Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech. 606, 225–237.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google ScholarPubMed
Hwang, J., Lee, J., Sung, H. J. & Zaki, T. A. 2016 Inner–outer interactions of large-scale structures in turbulent channel flow. J. Fluid Mech. 790, 128–157.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.CrossRefGoogle Scholar
Lee, J., Ahn, J. & Sung, H. J. 2015 Comparison of large-and very-large-scale motions in turbulent pipe and channel flows. Phys. Fluids 27 (2), 025101.CrossRefGoogle Scholar
Lee, J., Lee, J. H., Choi, J.-I. & Sung, H. J. 2014 Spatial organization of large-and very- large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.CrossRefGoogle Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lu, S. S. & Willmarth, W. W. 1973 Measurements of the structure of the Reynolds stress in a turbulent boundary layer. J. Fluid Mech. 60, 481–511.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31 (3), 418–428.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Morrill-Winter, C. & Klewicki, J. 2013 Influences of boundary layer scale separation on the vorticity transport contribution to turbulent inertia. Phys. Fluids 25 (1), 015108.Google Scholar
Nieuwstadt, F. T. M. & Bradshaw, P. 1997 Similarities and differences of turbulent boundary-layer, pipe and channel flow. In Boundary-Layer Separation in Aircraft Aerodynamics (ed. Henkes, R. A. W. M. & Bakker, P. G.), Delft University Press.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Theodorsen, T. 1952 Mechanism of turbulence. In Proceedings of the Second Midwestern Conference on Fluid Mechanics, pp. 1–18. Ohio State University.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54, 39–48.Google Scholar
Wei, T., Fife, P., Klewicki, J. & Mcmurtry, P. 2005 Properties of the mean momentum balance in turbulent boundary layer, pipe and channel flows. J. Fluid Mech. 522, 303–327.Google Scholar
Willmarth, W. W. & Lu, S. S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55, 65–92.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a 30R long turbulent pipe flow at R + = 685: large- and very large-scale motions. J. Fluid Mech. 698, 235–281.CrossRefGoogle Scholar