Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T02:03:06.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of Langmuir circulations on turbulence in the bottom boundary layer of shallow water

Published online by Cambridge University Press:  19 December 2018

Bing-Qing Deng Open the ORCID record for Bing-Qing Deng [Opens in a new window] ,
Zixuan Yang Open the ORCID record for Zixuan Yang [Opens in a new window] ,
Anqing Xuan  and
Lian Shen Open the ORCID record for Lian Shen [Opens in a new window]
Bing-Qing Deng
Affiliation:
St. Anthony Falls Laboratory and Department of Mechanical Engineering, University of Minnesota, Minneapolis, Minnesota 55455, USA
Zixuan Yang
Affiliation:
St. Anthony Falls Laboratory and Department of Mechanical Engineering, University of Minnesota, Minneapolis, Minnesota 55455, USA State Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, PR China
Anqing Xuan
Affiliation:
St. Anthony Falls Laboratory and Department of Mechanical Engineering, University of Minnesota, Minneapolis, Minnesota 55455, USA
Lian Shen*
Affiliation:
St. Anthony Falls Laboratory and Department of Mechanical Engineering, University of Minnesota, Minneapolis, Minnesota 55455, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Langmuir circulations (LCs) generated by the interaction between wind-driven currents and surface waves can engulf the whole water column in neutrally stratified shallow water and interact with the turbulence in the bottom boundary layer. In this study, we perform a mechanistic study using wall-resolved large-eddy simulations (LES) based on the Craik–Leibovich equations to investigate the effects of LCs on turbulence statistics in the bottom half of shallow water. The highest Reynolds number considered in this paper, 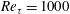$Re_{\unicode[STIX]{x1D70F}}=1000$, is larger than the values considered in wall-resolved LES studies of shallow-water Langmuir turbulence reported in literature. The logarithmic layer is diagnosed based on a plateau region in the profile of a diagnostic function. It is found that the logarithmic layer disrupted at 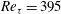$Re_{\unicode[STIX]{x1D70F}}=395$ reappears at 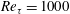$Re_{\unicode[STIX]{x1D70F}}=1000$, but the von Kármán constant is slightly different from the traditional value 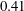$0.41$. To study the effects of LCs on turbulence statistics, LCs are extracted using streamwise averaging. The velocity fluctuations 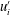$u_{i}^{\prime }$ are decomposed into a LC-coherent part 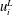$u_{i}^{L}$ and a residual turbulence part 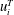$u_{i}^{T}$. It is found that the profiles of LC-coherent Reynolds shear stress 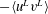$-\langle u^{L}v^{L}\rangle$ obtained at various Reynolds numbers are close to each other in the water-column coordinate 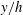$y/h$, with 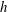$h$ being the half-water depth. As the Reynolds number (or, by definition, the ratio between the outer and inner length scales) increases, the influence of LCs on the near-bottom momentum transfer is reduced, which is responsible for the reappearance of the logarithmic layer. At all of the Reynolds numbers under investigation, the peaks of 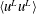$\langle u^{L}u^{L}\rangle$ are collocated in the water-column coordinate 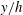$y/h$, while those of 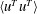$\langle u^{T}u^{T}\rangle$ are collocated in the inner-scale coordinate 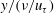$y/(\unicode[STIX]{x1D708}/u_{\unicode[STIX]{x1D70F}})$. Due to the increase in the distance between the peaks of 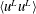$\langle u^{L}u^{L}\rangle$ and 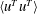$\langle u^{T}u^{T}\rangle$ with the Reynolds number, the profile of $\langle u^{\prime }u^{\prime }\rangle$ forms a bimodal shape at 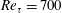$Re_{\unicode[STIX]{x1D70F}}=700$ and 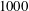$1000$.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 861 , 25 February 2019 , pp. 275 - 308
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afzal, N. & Yajnik, K. 1973 Analysis of turbulent pipe and channel flows at moderately large Reynolds number. J. Fluid Mech. 61, 23–31.Google Scholar
Akan, C., Tejada-Martínez, A. E., Grosch, C. E. & Martinat, G. 2013 Scalar transport in large-eddy simulation of Langmuir turbulence in shallow water. Cont. Shelf Res. 55, 1–16.Google Scholar
Alfredsson, P. H., Segalini, A. & Örlü, R. 2011 A new scaling for the streamwise turbulence intensity in wall-bounded turbulent flows and what it tells us about the ‘outer’ peak. Phys. Fluids 23, 041702.Google Scholar
Andrews, D. G. & McIntyre, M. E. 1978 An exact theory of nonlinear waves on a Lagrangian-mean flow. J. Fluid Mech. 89, 609–646.Google Scholar
Assaf, G., Gerard, R. & Gordon, A. L. 1971 Some mechanisms of oceanic mixing revealed in aerial photographs. J. Geophys. Res. Oceans 76, 6550–6572.Google Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & Garcia-Galache, J. P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1.Google Scholar
Bernardini, M., Pirozzoli, S. & Orlandi, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Blackwelder, R. F. & Eckelmann, H. 1979 Streamwise vortices associated with the bursting phenomenon. J. Fluid Mech. 94, 577–594.Google Scholar
Cabot, W. & Moin, P. 2000 Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow Turbul. Combust. 63, 269–291.Google Scholar
Chapman, D. R. 1979 Computational aerodynamics development and outlook. AIAA J. 17, 1293–1313.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24, 011702.Google Scholar
Craik, A. D. D. 1977 The generation of Langmuir circulations by an instability mechanism. J. Fluid Mech. 81, 209–223.Google Scholar
Craik, A. D. D. & Leibovich, S. 1976 A rational model for Langmuir circulations. J. Fluid Mech. 73, 401–426.Google Scholar
D’Asaro, E. A. 2014 Turbulence in the upper-ocean mixed layer. Annu. Rev. Mar. Sci 6, 101–115.Google Scholar
Dethleff, D. & Kemepema, E. W. 2007 Langmuir circulation driving sediment entrainment into newly formed ice: tank experiment results with application to nature (Lake Hattie, United States; Kara Sea, Siberia). J. Geophys. Res. Oceans 112, C02004.Google Scholar
Dierssen, H. M., Zimmerman, R. C., Drake, L. A. & Burdige, D. J. 2009 Potential export of unattached benthic macroalgae to the deep sea through wind-driven Langmuir circulation. Geophys. Res. Lett. 36, L04602.Google Scholar
Faller, A. J. & Caponi, E. A. 1978 Laboratory studies of wind-driven Langmuir circulations. J. Geophys. Res. Oceans 83, 3617–3633.Google Scholar
Farmer, D. & Li, M. 1995 Patterns of bubble clouds organized by Langmuir circulation. J. Phys. Oceanogr. 25, 1426–1440.Google Scholar
Gargett, A., Wells, J., Tejada-Martínez, A. E. & Grosch, C. E. 2004 Langmuir supercells: a mechanism for sediment resuspension and transport in shallow seas. Science 306, 1925–1928.Google Scholar
Gargett, A. E. & Grosch, C. E. 2014 Turbulence process domination under the combined forcings of wind stress, the Langmuir vortex force, and surface cooling. J. Phys. Oceanogr. 44 (1), 44–67.Google Scholar
Gargett, A. E., Savidge, D. K. & Wells, J. R. 2014 Anatomy of a Langmuir supercell event. J. Mar. Res. 72 (3), 127–163.Google Scholar
Gargett, A. E. & Wells, J. R. 2007 Langmuir turbulence in shallow water. Part 1. Observations. J. Fluid Mech. 576, 27–61.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 3, 1760–1765.Google Scholar
Golshan, R., Tejada-Martínez, A. E., Juha, M. J. & Bazilevs, Y. 2017 LES and RANS simulation of wind-and wave-forced oceanic turbulent boundary layers in shallow water with wall modeling. Comput. Fluids 142, 96–108.Google Scholar
Grosch, C. E. & Gargett, A. E. 2016 Why do LES of Langmuir supercells not include rotation? J. Phys. Oceanogr. 46 (12), 3595–3597.Google Scholar
Harcourt, R. R. 2013 A second-moment closure model of Langmuir turbulence. J. Phys. Oceanogr. 43 (4), 675–697.Google Scholar
Harcourt, R. R. & D’Asaro, E. A. 2008 Large-eddy simulation of Langmuir turbulence in pure wind seas. J. Phys. Oceanogr. 38, 1542–1562.Google Scholar
Holm, D. D. 1996 The ideal Craik–Leibovich equations. Physica D 98, 415–441.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to Re 𝜏 = 2003. Phys. Fluids 18, 011702.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. & Moser, R. D. 2007 What are we learning from simulating wall turbulence? Proc. R. Soc. Lond. A 365, 715–732.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kemp, P. H. & Simons, R. R. 1982 The interaction between waves and a turbulent current: waves propagating with the current. J. Fluid Mech. 116, 227–250.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59, 308–323.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Klewicki, J., Fife, P. & Wei, T. 2009 On the logarithmic mean profile. J. Fluid Mech. 638, 73–93.Google Scholar
Kukulka, T., Plueddemann, A. J. & Sullivan, P. P. 2012 Nonlocal transport due to Langmuir circulation in a coastal ocean. J. Geophys. Res. Oceans 117, C12007.Google Scholar
Kukulka, T., Plueddemann, A. J., Trowbridge, J. H. & Sullivan, P. P. 2010 Rapid mixed layer deepening by the combination of Langmuir and shear instabilities: a case study. J. Phys. Oceanogr. 40, 2381–2400.Google Scholar
Kukulka, T., Plueddemann, A. J., Trowbridge, J. H. & Sullivan, P. P. 2011 The influence of crosswind tidal currents on Langmuir circulation in a shallow ocean. J. Geophys. Res. Oceans 116, C08005.Google Scholar
Langmuir, I. 1938 Surface motion of water induced by wind. Science 87, 119–123.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Leibovich, S. 1977 On the evolution of the system of wind drift currents and Langmuir circulations in the ocean. Part 1. Theory and averaged current. J. Fluid Mech. 79, 715–743.Google Scholar
Leibovich, S. 1980 On wave–current interaction theories of Langmuir circulations. J. Fluid Mech. 99, 715–724.Google Scholar
Leibovich, S. 1983 The form and dynamics of Langmuir circulations. Annu. Rev. Fluid Mech. 15, 391–427.Google Scholar
Li, M., Garrett, C. & Skyllingstad, E. 2005 A regime diagram for classifying turbulent large eddies in the upper ocean. Deep Sea Res. I 52, 259–278.Google Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids 4, 633–635.Google Scholar
Longuet-Higgins, M. S. 1953 Mass transport in water waves. Proc. R. Soc. Lond. A 245, 535–581.Google Scholar
Luchini, P. 2017 Universality of the turbulent velocity profile. Phys. Rev. Lett. 118, 224501.Google Scholar
Manna, M., Vacca, A. & Verzicco, R. 2012 Pulsating pipe flow with large-amplitude oscillations in the very high frequency regime. Part 1. Time-averaged analysis. J. Fluid Mech. 700, 246–282.Google Scholar
Martinat, G., Grosch, C. E. & Gatski, T. B. 2014 Modeling of Langmuir circulation: triple decomposition of the Craik–Leibovich model. Flow Turbul. Combust. 92, 395–411.Google Scholar
Martinat, G., Xu, Y., Grosch, C. E. & Tejada-Martínez, A. E. 2011 LES of turbulent surface shear stress and pressure-gradient-driven flow on shallow continental shelves. Ocean Dyn. 61 (9), 1369–1390.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smiths, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
McWilliams, J. C., Huckle, E., Liang, J. & Sullivan, P. P. 2014 Langmuir turbulence in swell. J. Phys. Oceanogr. 44, 870–890.Google Scholar
McWilliams, J. C., Restrepo, J. M. & Lane, E. M. 2004 An asymptotic theory for the interaction of waves and currents in coastal waters. J. Fluid Mech. 511, 135–178.Google Scholar
McWilliams, J. C., Sullivan, P. P. & Moeng, C. H. 1997 Langmuir turbulence in the ocean. J. Fluid Mech. 334, 1–30.Google Scholar
Millikan, C. B. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the 5th International Congress on Applied Mechanics, Wiley.Google Scholar
Mizuno, Y. & Jiménez, J. 2011 Mean velocity and length-scales in the overlap region of wall-bounded turbulent flows. Phys. Fluids 23, 085112.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Nagib, H. M. & Chauhan, K. A. 2008 Variations of von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Nepf, H. M.1992 The production and mixing effects of Langmuir circulations. PhD thesis, Department of Civil Engineering, Stanford University.Google Scholar
Noh, Y., Min, H. S. & Raasch, S. 2004 Large eddy simulation of the ocean mixed layer: the effects of wave breaking and Langmuir circulation. J. Phys. Oceanogr. 34, 720–735.Google Scholar
Panton, R. L. 2001 Overview of the self-sustaining mechanisms of wall turbulence. Prog. Aerosp. Sci. 37, 341–383.Google Scholar
Phillips, O. M. 1967 The Dynamics of the Upper Ocean. Cambridge University Press.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Pollard, R. T. 1977 Observations and theolies of Langmuir circulations and their role in near surface mixing. In A Voyage of Discovery: George Deacon 70th Anniversary Volume, pp. 235–251. Pergamon Press.Google Scholar
Ramaprian, B. R. & Tu, S. W. 1983 Fully developed periodic turbulent pipe flow. Part 2. The detailed structure of the flow. J. Fluid Mech. 137, 59–81.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23 (1), 601–639.Google Scholar
Rotta, J. 1962 Turbulent boundary layers in incompressible flow. Prog. Aerosp. Sci. 2, 1–95.Google Scholar
Savidge, D. K. & Gargett, A. E. 2017 Langmuir supercells on the middle shelf of the South Atlantic Bight: 1. Cell structure. J. Mar. Res. 75 (2), 49–79.Google Scholar
Scagliarini, A., Einarsson, H., Gylfason, Á. & Toschi, F. 2015 Law of the wall in an unstably stratified turbulent channel flow. J. Fluid Mech. 781, R5.Google Scholar
Scott, J. T., Myer, G. E., Stewart, R. & Walther, E. G. 1969 On the mechanism of Langmuir circulations and their role in epilimnion mixing. Limnol. Oceanogr. 14, 493–503.Google Scholar
Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13, 1367–1384.Google Scholar
Sinha, N., Tejada-Martínez, A. E., Akan, C. & Grosch, C. E. 2015 Toward a K-profile parameterization of Langmuir turbulence in shallow coastal shelves. J. Phys. Oceanogr. 45 (12), 2869–2895.Google Scholar
Skyllingstad, E. D. & Denbo, D. W. 1995 An ocean large eddy simulation of Langmuir circulations and convection in the surface mixed layer. J. Geophys. Res. Oceans 100, 8501–8522.Google Scholar
Smith, J., Pinkel, R. & Weller, R. A. 1987 Velocity structure in the mixed layer during MILDEX. J. Phys. Oceanogr. 17, 425–439.Google Scholar
Smith, J. A. 2001 Observations and theories of Langmuir circulation: a story of mixing. In Fluid Mechanics and the Environment: Dynamical Approaches, pp. 295–314. Springer.Google Scholar
Sullivan, P. P. & McWilliams, J. C. 2010 Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 42, 19–42.Google Scholar
Sullivan, P. P., McWilliams, J. C. & Melville, W. K. 2007 Surface gravity wave effects in the oceanic boundary layer: large-eddy simulation with vortex force and stochastic breakers. J. Fluid Mech. 593, 405–452.Google Scholar
Sullivan, P. P., Romero, L., McWilliams, J. C. & Melville, W. K. 2012 Transient evolution of Langmuir turbulence in ocean boundary layers driven by hurricane winds and waves. J. Phys. Oceanogr. 42, 1959–1980.Google Scholar
Suzuki, N. & Fox-Kemper, B. 2016 Understanding Stokes forces in the wave–averaged equations. J. Geophys. Res. Oceans 121 (5), 3579–3596.Google Scholar
Tejada-Martínez, A. E., Akan, C., Sinha, N., Grosch, C. E. & Martinat, G. 2013 Surface dynamics in LES of full-depth Langmuir circulation in shallow water. Phys. Scr. 2013, 014008.Google Scholar
Tejada-Martínez, A. E. & Grosch, C. E. 2007 Langmuir turbulence in shallow water. Part 2. Large-eddy simulation. J. Fluid Mech. 576, 63–108.Google Scholar
Tejada-Martínez, A. E., Grosch, C. E., Sinha, N., Akan, C. & Martinat, G. 2012 Disruption of the bottom log layer in large-eddy simulations of full-depth Langmuir circulation. J. Fluid Mech. 699, 79–93.Google Scholar
Thorpe, S. A. 1992 The breakup of Langmuir circulation and the instability of an array of vortices. J. Phys. Oceanogr. 22, 350–360.Google Scholar
Thorpe, S. A. 2004 Langmuir circulation. Annu. Rev. Fluid Mech. 36, 55–79.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Walker, R., Tejada-Martínez, A. E. & Grosch, C. E. 2016 Large-eddy simulation of a coastal ocean under the combined effects of surface heat fluxes and full-depth Langmuir circulation. J. Phys. Oceanogr. 46 (8), 2411–2436.Google Scholar
Weller, R. A. & Price, J. F. 1988 Langmuir circulation within the oceanic mixed layer. Deep Sea Res. I 35, 711–747.Google Scholar
Zagarola, M. V., Perry, A. E. & Smits, A. J. 1997 Log laws or power laws: the scaling in the overlap region. Phys. Fluids 9, 2094–2100.Google Scholar