Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Strangfeld, C.
Müller-Vahl, H.
Nayeri, C. N.
Paschereit, C. O.
and
Greenblatt, D.
2016.
Airfoil in a high amplitude oscillating stream.
Journal of Fluid Mechanics,
Vol. 793,
Issue. ,
p.
79.
Motta, Valentina
Malzacher, Leonie
Neumann, Patrick
and
Peitsch, Dieter
2017.
Numerical Assessment of Virtual Control Surfaces for Compressor Blades.
Jost, Eva
Fischer, Annette
Bangga, Galih
Lutz, Thorsten
and
Krämer, Ewald
2017.
An investigation of unsteady 3-D effects on trailing edge flaps.
Wind Energy Science,
Vol. 2,
Issue. 1,
p.
241.
Motta, Valentina
Malzacher, Leonie
and
Peitsch, Dieter
2018.
Numerical Assessment of Virtual Control Surfaces for Load Alleviation on Compressor Blades.
Applied Sciences,
Vol. 8,
Issue. 1,
p.
125.
LI, Zhenyao
FENG, Lihao
KARBASIAN, Hamid Reza
WANG, Jinjun
and
KIM, Kyung Chun
2019.
Experimental and numerical investigation of three-dimensional vortex structures of a pitching airfoil at a transitional Reynolds number.
Chinese Journal of Aeronautics,
Vol. 32,
Issue. 10,
p.
2254.
Kaul, Upender K.
and
Nguyen, Nhan T.
2019.
A Correction Method for Unsteady Transonic Aerodynamics.
Kaul, Upender K.
and
Nguyen, Nhan T.
2019.
Extending A Correction Method for Unsteady Transonic Aerodynamics to Variable Camber Continuous Trailing Edge Flap.
Li, Xiao
Feng, Li-Hao
and
Li, Zhen-Yao
2019.
Flow mechanism for the effect of pivot point on the aerodynamic characteristics of a pitching airfoil and its manipulation.
Physics of Fluids,
Vol. 31,
Issue. 8,
Motta, Valentina
Malzacher, Leonie
Bicalho Civinelli de Almeida, Victor
Phan, Tien Dat
Liebich, Robert
Peitsch, Dieter
and
Quaranta, Giuseppe
2019.
A Physically Consistent Reduced Order Model for Plasma Aeroelastic Control on Compressor Blades.
Journal of Engineering for Gas Turbines and Power,
Vol. 141,
Issue. 9,
Brunner, C E
Kiefer, J
Hansen, MOL
and
Hultmark, M
2020.
Unsteady effects on a pitching airfoil at conditions relevant for large vertical axis wind turbines.
Journal of Physics: Conference Series,
Vol. 1618,
Issue. 5,
p.
052065.
Kaul, Upender K.
2021.
Resolving Pitching Airfoil Transonic Aerodynamics by Computational Fluid Dynamics Data Modeling1.
Journal of Fluids Engineering,
Vol. 143,
Issue. 9,
Neumann, P.
Motta, V.
Malzacher, L.
Phan, T. D.
Liebich, R.
Peitsch, D.
and
Quaranta, G.
2021.
Advances in Critical Flow Dynamics Involving Moving/Deformable Structures with Design Applications.
Vol. 147,
Issue. ,
p.
223.
S., Siva Viknesh
and
Poddar, Kamal
2021.
Active control of separated flow on a symmetric airfoil by pitching oscillation.
Physics of Fluids,
Vol. 33,
Issue. 8,
Bartholomay, Sirko
Wester, Tom T. B.
Perez-Becker, Sebastian
Konze, Simon
Menzel, Christian
Hölling, Michael
Spickenheuer, Axel
Peinke, Joachim
Nayeri, Christian N.
Paschereit, Christian Oliver
and
Oberleithner, Kilian
2021.
Pressure-based lift estimation and its application to feedforward load control employing trailing-edge flaps.
Wind Energy Science,
Vol. 6,
Issue. 1,
p.
221.
Ma, Ruwei
Yang, Yang
Li, Mingshui
and
Li, Qiusheng
2021.
The unsteady lift of an oscillating airfoil encountering a sinusoidal streamwise gust.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Choi, Woen-Sug
Jang, Won-Seok
Joe, Beom-Jin
Hong, Suk-Yoon
Song, Jee-Hun
and
Kwon, Hyun-Wung
2022.
Methods for assessing the ship rudder stability under lock-in phenomena considering fluid-structure interactions.
Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment,
Vol. 236,
Issue. 1,
p.
113.
Kaul, Upender K.
2023.
A Machine Learning Approach to Predicting Unsteady Transonic Flow of Pitching Airfoils.
Journal of Fluids Engineering,
Vol. 145,
Issue. 2,
Wei, Binbin
Gao, Yongwei
and
Hu, Shuling
2023.
Experimental and numerical study on dynamic stall under a large Reynolds number.
Advances in Aerodynamics,
Vol. 5,
Issue. 1,
Ahsan, Faraz
and
Todd Griffith, D.
2023.
Impact of Aerodynamic Modeling Assumptions on Flutter Speeds of Vertical-Axis Wind Turbines.
AIAA Journal,
Vol. 61,
Issue. 12,
p.
5377.
Torres, George L. S.
and
Marques, Flávio D.
2024.
Nonlinear geometric decomposition of airfoils into the thickness and camber contributions.
Meccanica,
Vol. 59,
Issue. 6,
p.
889.
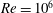 $\mathit{Re}=10^{6}$) flows.
$\mathit{Re}=10^{6}$) flows.


