Article contents
Inertial wave dynamics in a rotating liquid metal
Published online by Cambridge University Press: 25 July 2014
Abstract
The dynamics of free and forced inertial waves inside cylinders of different aspect ratios (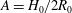 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A=H_0/2R_0$) were investigated experimentally in this study. The liquid metal GaInSn was chosen as the fluid in order to enable a contactless stimulation of the flow by means of alternating electromagnetic fields. A rotating magnetic field generates the rotating motion of the liquid, whereas periodic modulations of the field strength and short pulses excite specific wave modes. Ultrasound Doppler velocimetry was used to record the flow structure and to identify inertial waves in the set-up. Our experiments demonstrate selective excitation of different inertial wave modes by deliberate variation of the magnetic field parameters. Furthermore, it was found that turbulent perturbations in the boundary layers of the swirling flow are able to induce an inertial wave mode that survives over a long time. Experiments at the fundamental resonance have shown that multiple harmonic wave modes appeared simultaneously. The measured inertial wave frequencies were compared to the predictions of the linear inviscid theory.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A=H_0/2R_0$) were investigated experimentally in this study. The liquid metal GaInSn was chosen as the fluid in order to enable a contactless stimulation of the flow by means of alternating electromagnetic fields. A rotating magnetic field generates the rotating motion of the liquid, whereas periodic modulations of the field strength and short pulses excite specific wave modes. Ultrasound Doppler velocimetry was used to record the flow structure and to identify inertial waves in the set-up. Our experiments demonstrate selective excitation of different inertial wave modes by deliberate variation of the magnetic field parameters. Furthermore, it was found that turbulent perturbations in the boundary layers of the swirling flow are able to induce an inertial wave mode that survives over a long time. Experiments at the fundamental resonance have shown that multiple harmonic wave modes appeared simultaneously. The measured inertial wave frequencies were compared to the predictions of the linear inviscid theory.
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 11
- Cited by


