Published online by Cambridge University Press: 26 January 2017
We investigated experimentally the flow driven by a Lorentz force induced by an axial magnetic field 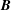 $\boldsymbol{B}$ and a radial electric current
$\boldsymbol{B}$ and a radial electric current 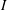 $I$ applied between two fixed concentric copper cylinders. The gap geometry corresponds to a rectangular section with an aspect ratio of
$I$ applied between two fixed concentric copper cylinders. The gap geometry corresponds to a rectangular section with an aspect ratio of 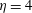 $\unicode[STIX]{x1D702}=4$ and we probe the azimuthal and axial velocity profiles of the flow along the vertical axis by using ultrasonic Doppler velocimetry. We have performed several runs at moderate magnetic field strengths, corresponding to moderate Hartmann numbers
$\unicode[STIX]{x1D702}=4$ and we probe the azimuthal and axial velocity profiles of the flow along the vertical axis by using ultrasonic Doppler velocimetry. We have performed several runs at moderate magnetic field strengths, corresponding to moderate Hartmann numbers 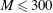 $M\leqslant 300$. At these forcing parameters and because of the geometry of our experimental device, we show that the inertial terms are not negligible and an azimuthal velocity that depends on both
$M\leqslant 300$. At these forcing parameters and because of the geometry of our experimental device, we show that the inertial terms are not negligible and an azimuthal velocity that depends on both 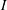 $I$ and
$I$ and 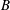 $B$ is induced. From measurements of the vertical velocity we focus on the characteristics of the secondary flow: the time-averaged velocity profiles are compatible with a secondary flow presenting two pairs of stable vortices, as pointed out by previous numerical studies. The flow exhibited a transition between two dynamical modes, a high- and a low-frequency one. The high-frequency mode, which emerges at low magnetic field forcing, corresponds to the propagation in the radial
$B$ is induced. From measurements of the vertical velocity we focus on the characteristics of the secondary flow: the time-averaged velocity profiles are compatible with a secondary flow presenting two pairs of stable vortices, as pointed out by previous numerical studies. The flow exhibited a transition between two dynamical modes, a high- and a low-frequency one. The high-frequency mode, which emerges at low magnetic field forcing, corresponds to the propagation in the radial  $r$-direction of tilted vortices. This mode is consistent with our previous experiments and with the instability described in Zhao et al. (Phys. Fluids, vol. 23 (8), 2011, 084103) taking place in an elongated duct geometry. The low-frequency mode, observed for high magnetic field forcing, consists of large excursions of the vortices. The dynamics of these modes matches the first axisymmetric instability described in Zhao & Zikanov (J. Fluid Mech., vol. 692, 2012, pp. 288–316) taking place in an square duct geometry. We demonstrated that this transition is controlled by the inertial magnetic thickness
$r$-direction of tilted vortices. This mode is consistent with our previous experiments and with the instability described in Zhao et al. (Phys. Fluids, vol. 23 (8), 2011, 084103) taking place in an elongated duct geometry. The low-frequency mode, observed for high magnetic field forcing, consists of large excursions of the vortices. The dynamics of these modes matches the first axisymmetric instability described in Zhao & Zikanov (J. Fluid Mech., vol. 692, 2012, pp. 288–316) taking place in an square duct geometry. We demonstrated that this transition is controlled by the inertial magnetic thickness 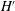 $H^{\prime }$ which is the characteristic length we introduce as a balance between the advection and the Lorentz force. The key point here is that when the inertial magnetic thickness
$H^{\prime }$ which is the characteristic length we introduce as a balance between the advection and the Lorentz force. The key point here is that when the inertial magnetic thickness 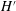 $H^{\prime }$ is comparable to one geometric characteristic length (
$H^{\prime }$ is comparable to one geometric characteristic length (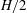 $H/2$ in the vertical or
$H/2$ in the vertical or 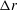 $\unicode[STIX]{x0394}r$ in the radial direction) the corresponding mode is favoured. Therefore, when
$\unicode[STIX]{x0394}r$ in the radial direction) the corresponding mode is favoured. Therefore, when 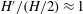 $H^{\prime }/(H/2)\approx 1$ we observe the high-frequency mode taking place in an elongated duct geometry, and when
$H^{\prime }/(H/2)\approx 1$ we observe the high-frequency mode taking place in an elongated duct geometry, and when 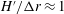 $H^{\prime }/\unicode[STIX]{x0394}r\approx 1$ we observe the low-frequency mode taking place in square duct geometry and high magnetic field.
$H^{\prime }/\unicode[STIX]{x0394}r\approx 1$ we observe the low-frequency mode taking place in square duct geometry and high magnetic field.