Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T12:49:37.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial migration of a spherical particle in laminar square channel flows from low to high Reynolds numbers

Published online by Cambridge University Press:  21 August 2015

Naoto Nakagawa ,
Takuya Yabu ,
Ryoko Otomo ,
Atsushi Kase ,
Masato Makino ,
Tomoaki Itano  and
Masako Sugihara-Seki
Naoto Nakagawa
Affiliation:
Department of Pure and Applied Physics, Kansai University, Suita, Osaka 564-8680, Japan
Takuya Yabu
Affiliation:
Department of Pure and Applied Physics, Kansai University, Suita, Osaka 564-8680, Japan
Ryoko Otomo
Affiliation:
Department of Mechanical Engineering, Kansai University, Suita, Osaka 564-8680, Japan
Atsushi Kase
Affiliation:
Department of Pure and Applied Physics, Kansai University, Suita, Osaka 564-8680, Japan
Masato Makino
Affiliation:
Department of Mechanical Systems Engineering, Yamagata University, Yonezawa, Yamagata 992-8510, Japan
Tomoaki Itano
Affiliation:
Department of Pure and Applied Physics, Kansai University, Suita, Osaka 564-8680, Japan
Masako Sugihara-Seki*
Affiliation:
Department of Pure and Applied Physics, Kansai University, Suita, Osaka 564-8680, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

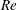The lateral migration properties of a rigid spherical particle suspended in a pressure-driven flow through channels with square cross-sections were investigated numerically, in the range of Reynolds numbers ($Re$) from 20 to 1000. The flow field around the particle was computed by the immersed boundary method to calculate the lateral forces exerted on the particle and its trajectories, starting from various initial positions. The numerical simulation showed that eight equilibrium positions of the particle are present at the centres of the channel faces and near the corners of the channel cross-section. The equilibrium positions at the centres of the channel faces are always stable, whereas the equilibrium positions at the corners are unstable until 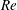$Re$ exceeds a certain critical value, 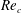$Re_{c}$. At 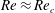$Re\approx Re_{c}$, additional equilibrium positions appear on a heteroclinic orbit that joins the channel face and corner equilibrium positions, and the lateral forces along the heteroclinic orbit are very small. As 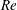$Re$ increases, the channel face equilibrium positions are shifted towards the channel wall at first, and then shifted away from the channel wall. The channel corner equilibrium positions exhibit a monotonic shift towards the channel corner with increasing 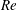$Re$. Migration behaviours of the particle in the cross-section are also predicted for various values of 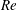$Re$. These numerical results account for the experimental observations of particle distributions in the cross-section of micro and millimetre scale channels, including the characteristic alignment and focusing of the particles, the absence of the corner equilibrium positions at low 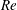$Re$ and the progressive shift of the equilibrium positions with 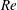$Re$.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 779 , 25 September 2015 , pp. 776 - 793
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbas, M., Magaud, P., Gao, Y. & Geoffroy, S. 2014 Migration of finite sized particles in a laminar square channel flow from low to high Reynolds numbers. Phys. Fluids 26, 123301.CrossRefGoogle Scholar
Asmolov, E. S. 1999 The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87.Google Scholar
Bhagat, A. A. S., Kuntaegowdanahalli, S. S. & Papautsky, I. 2008 Enhanced particle filtration in straight microchannels using shear-modulated inertial migration. Phys. Fluids 20, 101702.Google Scholar
Bird, R. B., Stewart, W. & Lightfoot, E. 2007 Transport Phenomena, 2nd edn. p. 187. Wiley.Google Scholar
Choi, Y., Seo, K. & Lee, S. 2011 Lateral and cross-lateral focusing of spherical particles in a square microchannel. Lab on a Chip 11, 460–465.Google Scholar
Chun, B. & Ladd, A. J. C. 2006 Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions. Phys. Fluids 18, 031704.Google Scholar
Ciftlick, A. T., Ettori, M. & Gijs, M. A. M. 2013 High throughput-per-footprint inertial focusing. Small 9, 2764–2773.CrossRefGoogle Scholar
Di Carlo, D. 2009 Inertial microfluidics. Lab on a Chip 9, 3038–3046.Google Scholar
Di Carlo, D., Edd, J. F., Humphry, K. J., Stone, A. H. & Toner, M. 2009 Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 102, 094503.Google Scholar
Di Carlo, D., Irima, D., Tompkins, R. G. & Toner, M. 2007 Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl Acad. Sci. USA 104, 18892–18897.Google Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a newtonian fluid. Part 2. Couette flow and Poiseuille flow. J. Fluid Mech. 277, 271–301.CrossRefGoogle Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flow. J. Fluid Mech. 65, 365–400.Google Scholar
Hood, K., Lee, S. & Roper, M. 2015 Inertial migration of a rigid sphere in three-dimensional Poiseuille flow. J. Fluid Mech. 765, 452–479.CrossRefGoogle Scholar
Humphry, K. J., Kulkami, P. M., Weitz, D. A., Morris, J. F. & Stone, H. A. 2010 Axial and lateral particle ordering in finite Reynolds number channel flows. Phys. Fluids 22, 081703.CrossRefGoogle Scholar
Kajishima, T., Takiguchi, S., Hamasaki, H. & Miyake, Y. 2001 Turbulence structure of particle-laden flow in a vertical plane channel due to vortex shedding. JSME J. B 44, 526–535.Google Scholar
Kim, Y. W. & Yoo, J. Y. 2008 The lateral migration of neutrally-buoyant spheres transported through square microchannels. J. Micromech. Microengng 18, 065015.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2004a Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 515, 171–195.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2004b Lateral forces on a sphere. Oil Gas Sci. Tech. Rev. JFP 59, 59–70.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2009 Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 621, 59–67.Google Scholar
Miura, K., Harada, S., Itano, T. & Sugihara-Seki, M. 2015 Inertial migration of spheres in square channel flows. Kyoto University RIMS Kokyuroku 1940, 68–75 (in Japanese).Google Scholar
Miura, K., Itano, T. & Sugihara-Seki, M. 2014 Inertial migration of neutrally buoyant spheres in a pressure-driven flow through square channels. J. Fluid Mech. 749, 320–330.Google Scholar
Nakagawa, N., Miura, K., Otamo, R., Makino, M. & Sugihara-Seki, M.2014 Lateral migration of a spherical particle in channel flow. WCCM XI, ECCM V, ECFD VI. MS007C.Google Scholar
Nakayama, Y. & Yamamoto, R. 2005 Simulation method to resolve hydrodynamic interactions in colloidal dispersions. Phys. Rev. E 71, 036707.Google Scholar
Schonberg, J. A. & Hinch, E. J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517–524.Google Scholar
Segre, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.Google Scholar
Segre, G. & Silberberg, A. 1962 Behaviour of macroscopic rigid spheres in Poiseuille flow. Part 2. Experimental results and interpretation. J. Fluid Mech. 14, 136–157.CrossRefGoogle Scholar
Sugihara-Seki, M.2015 Inertial migration of spherical particles in channel flows. Nagare 34 (in press).Google Scholar