Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T04:59:26.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial instability of intense stratified anticyclones. Part 2. Laboratory experiments

Published online by Cambridge University Press:  06 September 2013

Ayah Lazar ,
A. Stegner ,
R. Caldeira ,
C. Dong ,
H. Didelle  and
S. Viboud
Ayah Lazar*
Affiliation:
Department of Geophysics and Planetary Science, Tel Aviv University, Tel Aviv, Tel Aviv 69978, Israel Laboratoire de Météorologie Dynamique, École Polytechnique, 91128 Palaiseau CEDEX, France
A. Stegner
Affiliation:
Laboratoire de Météorologie Dynamique, École Polytechnique, 91128 Palaiseau CEDEX, France UME, ENSTA Centre de l’Yvette, Chemin de la Hunière, 91761 Palaiseau CEDEX, France
R. Caldeira
Affiliation:
CIIMAR – Interdisciplinary Centre of Marine and Environmental Research, 289 Rua dos Bragas, 4050-123 Porto, Portugal
C. Dong
Affiliation:
Institute of Geophysics and Planetary Physics, University of California, 603 Charles E. Young Drive, East, Los Angeles, CA 90095-1567, USA
H. Didelle
Affiliation:
LEGI/Coriolis, 21 Avenue des Martyrs, 38000 Grenoble, France
S. Viboud
Affiliation:
LEGI/Coriolis, 21 Avenue des Martyrs, 38000 Grenoble, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Large-scale laboratory experiments were performed on the Coriolis rotating platform to study the stability of intense vortices in a thin stratified layer. A linear salt stratification was set in the upper layer on top of a thick barotropic layer, and a cylinder was towed in the upper layer to produce shallow cyclones and anticyclones of similar size and intensity. We focus our investigations on submesoscale eddies, where the radius is smaller than the baroclinic deformation radius. 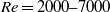Towing speed, cylinder size and stratification were changed in order to cover a large range of the parameter space, staying in a relatively high horizontal Reynolds number ($Re= 2000{{\unicode{x2013}}}7000$). The Rayleigh criterion states that inertial instabilities should strongly destabilize intense anticyclonic eddies if the vorticity in the vortex core is negative enough 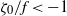${\zeta }_{0} / f\lt - 1$, where 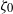${\zeta }_{0} $ is the relative vorticity in the core of the vortex, and 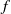$f$ is the Coriolis parameter. However, we found that some anticyclones remain stable even for very intense negative vorticity values, up to 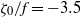${\zeta }_{0} / f= - 3. 5$, when the Burger number is large enough. This is in agreement with the linear stability analysis performed in part 1 (J. Fluid Mech., vol. 732, 2013, pp. 457–484), which shows that the combined effect of a strong stratification and a moderate vertical dissipation may stabilize even very intense anticyclones, and the unstable eddies we found were located close to the marginal stability limit. Hence, these experimental results agree well with the simple stability diagram proposed in the Rossby, Burger and Ekman parameter space for inertial destabilization of viscous anticyclones within a shallow and stratified layer.

JFM classification

Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , pp. 485 - 509
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afanasyev, Y. D. 2002 Experiments on instability of columnar vortex pairs in rotating fluid. Geophys. Astrophys. Fluid Dyn. 96 (1), 31–48.CrossRefGoogle Scholar
Afanasyev, Y. D. & Peltier, W. R. 1998 Three-dimensional instability of anticyclonic swirling flow in rotating fluid: laboratory experiments and related theoretical predictions. Phys. Fluids 10 (12), 3194–3202.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.CrossRefGoogle Scholar
Boyer, D. L. & Kmetz, M. L. 1983 Vortex shedding in rotating flows. Geophys. Astrophys. Fluid Dyn. 26 (1/2), 51–83.Google Scholar
Cambon, C., Benoit, J.-P., Shao, L. & Jacquin, L. 2006 Stability analysis and large-eddy simulation of rotating turbulence with organized eddies. J. Fluid Mech. 278 (1), 175.CrossRefGoogle Scholar
Capet, X., McWilliams, J. C., Molemaker, M. J. & Shchepetkin, A. F. 2008 Mesoscale to submesoscale transition in the California current system. Part 1. Flow structure, eddy flux, and observational tests. J. Phys. Oceanogr. 38 (1), 29–43.Google Scholar
Carnevale, G. F., Kloosterziel, R. C., Orlandi, P. & van Sommeren, D. D. J. A. 2011 Predicting the aftermath of vortex breakup in rotating flow. J. Fluid Mech. 669, 90–119.Google Scholar
Chavanne, C., Flament, P. & Gurgel, K.-W. 2010 Interactions between a submesoscale anticyclonic vortex and a front. J. Phys. Oceanogr. 40 (8), 1802–1818.Google Scholar
Dong, C., McWilliams, J. C. & Shchepetkin, A. F. 2007 Island wakes in deep water. J. Phys. Oceanogr. 37 (4), 962–981.Google Scholar
D’Orgeville, M. & Hua, B. L. 2005 Equatorial inertial-parametric instability of zonally symmetric oscillating shear flows. J. Fluid Mech. 531, 261–291.Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551 (1), 235.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Three-dimensional instability of isolated vortices. Phys. Fluids 15 (8), 2113–2126.Google Scholar
Griffiths, S. D. 2003 The nonlinear evolution of zonally symmetric equatorial inertial instability. J. Fluid Mech. 474, 245–273.Google Scholar
Griffiths, S. D. 2008 The limiting form of inertial instability in geophysical flows. J. Fluid Mech. 605, 115–143.Google Scholar
Hua, B. L., Moore, D. W. & Le Gentil, S. 1997 Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 331, 345–371.Google Scholar
Klein, P., Hua, B. L., Lapeyre, G., Capet, X., Le Gentil, S. & Sasaki, H. 2008 Upper ocean turbulence from high-resolution 3D simulations. J. Phys. Oceanogr. 38 (8), 1748.CrossRefGoogle Scholar
Kloosterziel, R. C., Carnevale, G. F. & Orlandi, P. 2007 Inertial instability in rotating and stratified fluids: barotropic vortices. J. Fluid Mech. 583, 379–412.Google Scholar
Kloosterziel, R. C. & van Heijst, G. J. F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.Google Scholar
Lazar, A., Stegner, A. & Heifetz, E. 2013 Inertial instability of intense stratified anticyclones. Part 1. Generalized stability criterion. J. Fluid Mech. 732, 457–484.Google Scholar
Le Bars, M., Le Dizès, S. & Le Gal, P. 2007 Coriolis effects on the elliptical instability in cylindrical and spherical rotating containers. J. Fluid Mech. 585, 323–342.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Capet, X. 2010 Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 654, 35–63.CrossRefGoogle Scholar
Mutabazi, I., Normand, C. & Wesfreid, J. E. 1992 Gap size effects on centrifugally and rotationally driven instabilities. Phys. Fluids A 4, 1199–1205.Google Scholar
Orlandi, P. & Carnevale, G. F. 1999 Evolution of isolated vortices in a rotating fluid of finite depth. J. Fluid Mech. 381, 239–269.Google Scholar
Oster, G. 1965 Density gradients. Sci. Am. 213 (2), 70–76.CrossRefGoogle Scholar
Perret, G., Stegner, A., Farge, M & Pichon, T 2006 Cyclone–anticyclone asymmetry of large-scale wakes in the laboratory. Phys. Fluids 18, 036603.CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in a barotropic shear. Phys. Fluids 21 (10), 106601.Google Scholar
Potylitsin, P. G. & Peltier, W. R. 1998 Stratification effects on the stability of columnar vortices on the $f$ -plane. J. Fluid Mech. 355, 45–79.Google Scholar
Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional vortex dipoles. Phys. Fluids 12 (2), 245–248.CrossRefGoogle Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comp. Fluid Dyn. 11 (3/4), 305–322.Google Scholar
Stegner, A., Pichon, T. & Beunier, M. 2005 Elliptical-inertial instability of rotating Kármán vortex streets. Phys. Fluids 17 (6), 066602.Google Scholar
Tarbouriech, L. & Renouard, D. 1996 Stabilisation et déstabilisation par la rotation d’un sillage plan turbulent. C. R. Acad. Sci. 323, 391–396.Google Scholar
Taylor, J. R. & Ferrari, R. 2009 On the equilibration of a symmetrically unstable front via a secondary shear instability. J. Fluid Mech. 622, 103–113.CrossRefGoogle Scholar
Teinturier, S., Stegner, A., Didelle, H. & Viboud, S. 2010 Small-scale instabilities of an island wake flow in a rotating shallow-water layer. Dyn. Atmos. Oceans 49, 1–30.Google Scholar

Lazar et al. supplementary movie

The surface vorticity field, normalised by the Coriolis parameter, for experiment 10. This is the whole movie of the snapshots shown in figure 7.

Download Lazar et al. supplementary movie(Video)
Video 10.3 MB