Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-01T03:59:48.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial effects on the rheology of a dilute emulsion

Published online by Cambridge University Press:  08 March 2010

R. VIVEK RAJA ,
GANESH SUBRAMANIAN  and
DONALD L. KOCH
R. VIVEK RAJA
Affiliation:
Department of Mechanical Engineering, NIT Tiruchirappalli, Tamil Nadu, 620015, India
GANESH SUBRAMANIAN*
Affiliation:
Engineering Mechanics Unit, JNCASR, Jakkur, Bangalore, 560064, India
DONALD L. KOCH
Affiliation:
School of Chemical and Bio-Molecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The behaviour of an isolated nearly spherical drop in an ambient linear flow is examined analytically at small but finite Reynolds numbers, and thereby the first effects of inertia on the bulk stress in a dilute emulsion of neutrally buoyant drops are calculated. The Reynolds numbers, Re = a2ρ/μ and 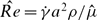, are the relevant dimensionless measures of inertia in the continuous and disperse(drop) phases, respectively. Here, a is the drop radius, is the shear rate, ρ is the common density and 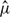and μ are, respectively, the viscosities of the drop and the suspending fluid. The assumption of nearly spherical drops implies the dominance of surface tension, and the analysis therefore corresponds to the limit of the capillary number(Ca) based on the viscosity of the suspending fluid being small but finite; in other words, Ca ≪ 1, where Ca = μa/T, T being the coefficient of interfacial tension. The bulk stress is determined to O(φRe) via two approaches. The first one is the familiar direct approach based on determining the force density associated with the disturbance velocity field on the surface of the drop; the latter is determined to O(Re) from a regular perturbation analysis. The second approach is based on a novel reciprocal theorem formulation and allows the calculation, to O(Re), of the drop stresslet, and hence the emulsion bulk stress, with knowledge of only the leading-order Stokes fields. The first approach is used to determine the bulk stress for linear flows without vortex stretching, while the reciprocal theorem approach allows one to generalize this result to any linear flow. For the case of simple shear flow, the inertial contributions to the bulk stress lead to normal stress differences(N1, N2) at O(φRe), where φ(≪1) is the volume fraction of the disperse phase. Inertia leads to negative and positive contributions, respectively, to N1 and N2 at O(φRe). The signs of the inertial contributions to the normal stress differences may be related to the O(ReCa) tilting of the drop towards the velocity gradient direction. These signs are, however, opposite to that of the normal stress differences in the creeping flow limit. The latter are O(φCa) and result from an O(Ca2) deformation of the drop acting to tilt it towards the flow axis. As a result, even a modest amount of inertia has a significant effect on the rheology of a dilute emulsion. In particular, both normal stress differences reverse sign at critical Reynolds numbers(Rec) of O(Ca) in the limit Ca ≪ 1. This criterion for the reversal in the signs of N1 and N2 is more conveniently expressed in terms of a critical Ohnesorge number(Oh) based on the viscosity of the suspending fluid, where Oh = μ/(ρaT)1/2. The critical Ohnesorge number for a sign reversal in N1 is found to be lower than that for N2, and the precise numerical value is a function of λ. In uniaxial extensional flow, the Trouton viscosity remains unaltered at O(φRe), the first effects of inertia now being restricted to O(φRe3/2). The analytical results for simple shear flow compare favourably with the recent numerical simulations of Li & Sarkar (J. Rheol., vol. 49, 2005, p. 1377).

Type
Papers
Information
Journal of Fluid Mechanics , Volume 646 , 10 March 2010 , pp. 255 - 296
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Barthes Biesel, D. & Acrivos, A. 1973 Deformation and burst of a liquid droplet freely suspended in a linear shear field. J. Fluid Mech. 61, 1.CrossRefGoogle Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545.CrossRefGoogle Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids, vol. 1. Wylie.Google Scholar
Esmaeeli, A. & Tryggvason, G. 1998 Direct numerical simulations of bubbly flows. Part 1. Low Reynolds number arrays. J. Fluid Mech. 377, 313.CrossRefGoogle Scholar
Frankel, N. A. & Acrivos, A. 1970 The constitutive equation for a dilute emulsion. J. Fluid Mech. 44, 68.CrossRefGoogle Scholar
Greco, F. 2002 Second-order theory for the deformation of a Newtonian drop in a stationary flow field, Phys. Fluids 14 (3), 946.CrossRefGoogle Scholar
Ho, B. P. & Leal, L. G. 1974 Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 65, 365.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Koch, D. L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newt. Fluid Mech. 138, 87.CrossRefGoogle Scholar
Larson, R. G. 1988 Constitutive Equations for Polymer Melts and Solutions. Butterworth.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12, 435.CrossRefGoogle Scholar
Leal, L. G. 1992 Laminar Flow and Convective Transport Processes. Butterworth-Heineman.Google Scholar
Li, X. & Sarkar, K. 2005 Effects of inertia on the rheology of a dilute emulsion of viscous drops in steady shear. J. Rheol. 49, 1377.CrossRefGoogle Scholar
Lin, C. J., Peery, J. H. & Schowalter, W. R. 1970 Simple shear flow around a rigid sphere: inertial effects and suspension rheology. J. Fluid Mech. 44, 1.CrossRefGoogle Scholar
Lumley, J. L. 1970 Toward a turbulent constitutive relation. J. Fluid Mech. 41, 314.CrossRefGoogle Scholar
Mikulencak, D. R. & Morris, J. F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215.CrossRefGoogle Scholar
Morris, J. F. & Brady, J. F. 1998 Pressure-driven flow of a suspension: buoyancy effects. Intl J. Multiphase flow 24 (1), 105.CrossRefGoogle Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven suspension flow: simulation and theory. J. Fluid Mech. 275, 157.CrossRefGoogle Scholar
Peery, J. H. 1966 Fluid mechanics of rigid and deformable particles in shear flows at low Reynolds numbers. PhD thesis, Princeton University.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237.CrossRefGoogle Scholar
Ramaswamy, S. & Leal, L. G. 1997 A note on inertial effects in the deformation of Newtonian drops in a uniaxial extensional flow. Intl J. Multiphase Flow 23 (3), 561.CrossRefGoogle Scholar
Renardy, Y. Y. & Cristini, V. 2001 Effect of inertia on drop breakup under shear. Phys. Fluids 13 (1), 7.CrossRefGoogle Scholar
Ryskin, G. 1980 The extensional viscosity of a dilute suspension of spherical particles at intermediate microscale Reynolds numbers. J. Fluid Mech. 99, 513.CrossRefGoogle Scholar
Schonberg, J. A. & Hinch, E. J. 1989 Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 203, 517.CrossRefGoogle Scholar
Schowalter, W. R., Chaffey, C. E. & Brenner, H. 1968 Rheological behaviour of a dilute emulsion. J. Colloid Interface Sci. 26, 152.CrossRefGoogle ScholarPubMed
Sherwood, J. D. 1980 The primary electroviscous effect in a suspension of spheres. J. Fluid Mech. 101, 609.CrossRefGoogle Scholar
Stone, H. A., Brady, J. F. & Lovalenti, P. M. 2000 Inertial effects on the rheology of suspensions and on the motion of individual particles. J. Fluid Mech. (submitted).Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2006 Inertial effects in the transfer of heat or mass from neutrally buoyant spheres in a steady linear flow field. Phys. Fluids 18, 073302.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2010 The influence of the inertially dominated outer region on the rheology of a dilute dispersion of low-Reynolds-number drops or rigid particles. J. Fluid Mech. (submitted).CrossRefGoogle Scholar
Taylor, G. I. 1932 The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. A 146, 501.Google Scholar
Vasseur, P. & Cox, R. G. 1976 The lateral migration of a spherical particle in a two-dimensional shear flow. J. Fluid Mech. 78, 385.CrossRefGoogle Scholar
Vlahovska, P. M., Loewenberg, M. & Blawzdziewicz, J. 2005 Deformation of a surfactant-covered drop in a linear flow. Phys. Fluids 17, 103103.CrossRefGoogle Scholar
Wang, L. Y., Yin, X., Koch, D. L. & Cohen, C. 2009 Hydrodynamic diffusion and mass transfer across a sheared suspension of neutrally buoyant particles. Phys. fluids 21, 033303.CrossRefGoogle Scholar